抛硬币十次正面，第十一次正面的概率是多少？ | AlgorithmDog
我们抛硬币，前十次都是正面，那么第十一次正面的概率是多少？
看到上图，估计大伙已经知道我在吐槽啥了。一种答案是50%，另一种答案是。
1. 联合概率和条件概率
抛硬币是一个典型的伯努利过程。硬币正面朝上的概率用表示，抛的次数用 n 表示，正面的次数用 t 表示，表示第 i 次硬币正面。
第十一次为正面的概率是多少？这个问题首先是一道语文题。我们得搞清楚，当我们问第十一次为正面的概率是多少，我们到底问了啥。回答的人，认为问题是条件概率或者是(和前面结果独立)。回答的人，认为问题是联合概率。
明确条件概率和联合概率概念之后，“第十一次正面的概率是多少（在前面十次正面的情况下）？” 是在问条件概率，而不是问联合概率。因此这不是一个数学题，而是一个语文题。
2. 贝叶斯
在生活场景下，回答第十一次正面的概率 0.5 是 OK 的。因此在生活中，我们一般认为硬币是无偏的。不过贝叶斯学派的童鞋们有不同的话说。如果抛硬币正面的概率，那么前面十次都是正面的概率就是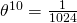 
。不太可能吧，那么小的概率都被我们碰到。因此贝叶斯的童鞋们认为，这个硬币倾向于正面。
在抛硬币问题上，贝叶斯公式如下所示。
(1) 
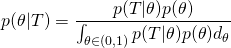
按照这个公式，贝叶斯关心概率的概率。计算这个概率的概率之前，我们需要先验概率。对于抛硬币这个伯努利过程，一般用 Beta 分布做先验概率，Beta 分布的公式如下所示。
(2) 
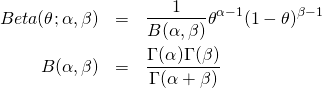
其中和是 Beta 分布的两个参数。计算的后验概率。
(3) 
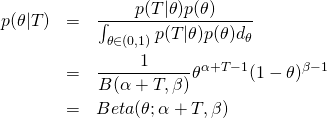
概率密度分布示意图如下所示。
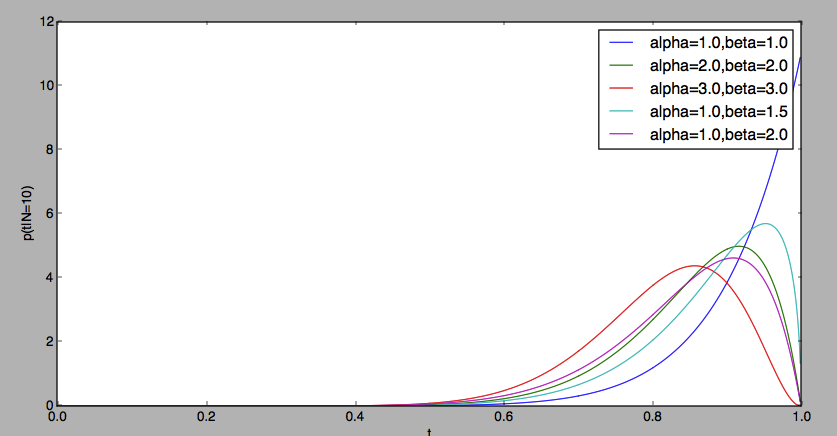
那么按照贝叶斯方法，第十一次正面的概率是多少？不好意思，贝叶斯方法并不能计算出这个，但贝叶斯方法能够计算后验概率。根据后验概率，我们能计算以一定的概率处于一定范围。
3. 区间估计
其实我们还可以用区间估计来解决这个问题。针对参数, 区间估计算出一个区间 [,]，其中是两个统计量。随机区间 [,] 覆盖参数的概率被称为覆盖概率，表示为。覆盖概率的最小值被称为置信度，表示为。对于置信度为 1-的区间估计，我们有
(4) 
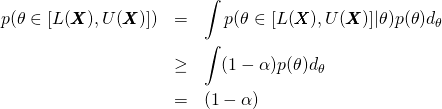
其中是未知的先验概率。相比贝叶斯的做法，区间估计不需要具体的先验概率。按照上面的公式，参数在区间的可能性大于 1 –。
虽然伯努利过程简单，但相关的区间估计都有缺陷。相关的区间估计包括 Wald interval、Wilson score interval、Jeffreys interval、Clopper-Pearson interval 和 Agresti-Coull Interval 等等。我们用适用于极端情况的 Wilson score interval 做例子。Wilson score interval 的计算公式如下所示。
(5) 
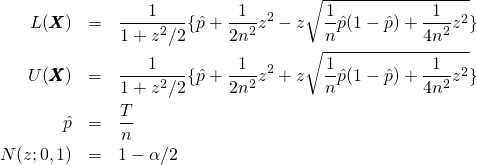
我们用模拟方法计算 Wilson score interval 的覆盖概率，其中参数设置为，结果如下图所示。可以发现覆盖概率有时会低于置信度，说明 Wilson score interval 存在缺陷。这时我们不能说: 至少 1-的可能性，参数属于 Wilson score interval。不过我们也发现，覆盖概率一直保持较高的水平。我们很有信心属于 Wilson score interval。
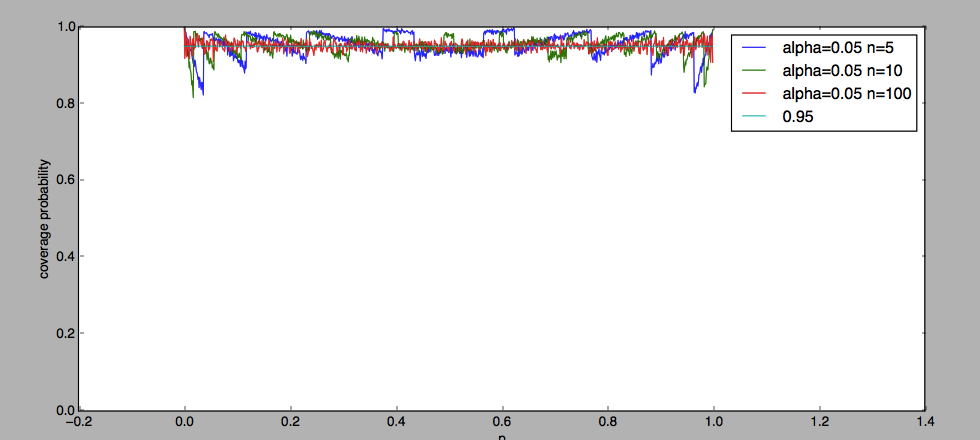
回到之前的问题。抛了十次全部为正，则。再令。按照公式计算得，即得区间 [0.722,1]。我们很有信心地认为第十一次正面的概率处于 0.722 和 1 之间。
4. 总结
当然啦，硬币可能立起来，哈哈哈。
最后欢迎关注我的公众号 AlgorithmDog，每周的更新就会有提醒哦~
正文到此结束
热门推荐
相关文章
近期评论
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
搞个gitee的项目
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
