Houdini 缠绕美女 之 反弹原理应用以及生成穿过控制点的Bezier曲线

前几天看到机器猫的一片博客讲到了用曲线填充几何体的方法，其中很受启发的地方是按照他的叫做“弹弹弹”的方法，其实就是raytrace的一个物理上的实现。这里是原博客地址： http://blog.csdn.net/cuckon/article/details/43710653

他应该是在maya里面实现的这一方法，出于好奇于是尝试看能不能在Houdini里面也作出类似的效果出来，纯粹是照虎画猫了。这是完成的效果图：

float radius = 1000; int maxIterate = ch("maxNumber"); vector origPosition = point(geoself(), "P", 0); vector origNormal = point(geoself(), "N", 0); origNormal *= radius; //get the reflection normal direction vector getReflection(vector origPosition; vector nextPosition; int primNum){  vector direction, primNormal;  vector reflect;  direction = normalize(nextPosition - origPosition);  primNormal = prim(1, "N", primNum);  reflect = reflect(direction, primNormal);  return reflect; } int flag = 0; while(flag < maxIterate){   int primNum;   int pointNum;   float u, v;   vector nextPosition,nextNormal;   //find the intersection point   primNum = intersect(1, origPosition, origNormal, nextPosition, u, v);   if(primNum != -1){     i@primNum = primNum;    pointNum = addpoint(geoself(), nextPosition);    nextNormal = getReflection(origPosition, nextPosition, primNum);    setattrib(geoself(), "point", "N", pointNum, 0, nextNormal, "set");    //extend the original position out of the surface a little bit    //this way can avoid some errors from the intersection    origPosition = nextPosition + normalize(nextNormal)*0.00001;    origNormal = normalize(nextNormal) * radius;   }if(primNum == -1){    break;   }   flag += 1; }  

2：第二个问题是把计算出来的点用曲线的方式穿起来。个人感觉其实这才是这个效果的难点地方，vex里面没有提供在几何体级别下操作曲线的方法，但是hou模块中有直接操作曲线的createNURBSCurve和createBezierCurve，顺着这个思路，那么接下来的工作就绪要转入到python中去进行了。最开始的时候我使用了createNURBSCurve这个函数来把所有之前生成的点连接起来，但是有一个很大的问题就是除了起点和末点其他点都不在曲线身上，虽然这是NURBS的特点，但效果肯定不能使用这个方法。为了解决这个问题也查找了不少资料，最后确定在了BezierCurve曲线上面，这是一个非常特殊的样条曲线，可以理解为BezierCurve是B样条曲线的特例，而B样条曲线是NURBS的一个特例。而且正好hou模块里面有生成这个曲线的方法，如下图：

使用的要求就是非闭合曲线的生成点数量必须满足3n+1，其中曲线会穿过3n的点，其他点都会成为权重点。另外为了达到穿过这些点的时候曲线的曲率是连续的，权重点和对应穿过的点必须保证在同一条直线上。基于这些条件下图为我能想到的实现方法：

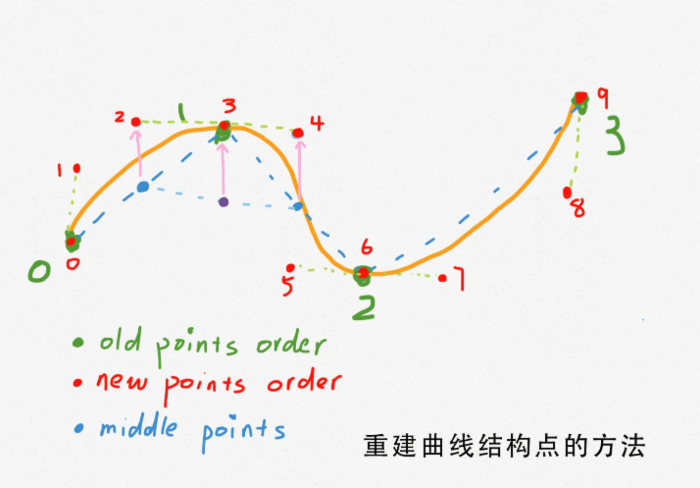
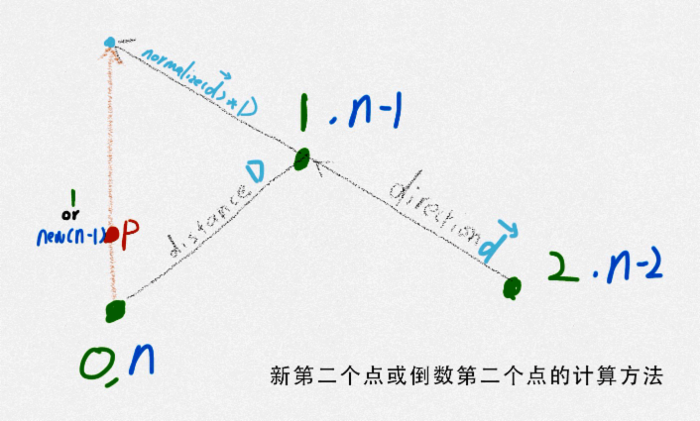
运用这个模型开始在python里面添加新的点，从而使生成的曲线能够穿过之前“弹”出来的点，下面是在python中的代码：

node = hou.pwd() geo = node.geometry() #get the weight value from the interface weight = node.evalParm("weight") # Add code to modify contents of geo. # Use drop down menu to select examples. #get all the point instances from the geo itself points = geo.points() pointNum = len(points) #define the up direction for cross product up = hou.Vector3(0, 1, 0) #put all the new points in this list newPointList = [] # the function to get the center point between two positions def getCenterPosition(firstPosition, secondPosition):  centerPosition = (firstPosition + secondPosition) * 0.5  return centerPosition #the function to get the second or last second point position  def getSecondPosition(currentPosition, nextPosition, thirdPosition):  mirrorDirection = nextPosition - thirdPosition  tmpDirection = currentPosition - nextPosition  mirrorLength = tmpDirection.length()  mirrorPosition = mirrorLength * mirrorDirection.normalized() + nextPosition  secondPosition = (getCenterPosition(mirrorPosition, currentPosition) - currentPosition) * 0.2 + currentPosition  return secondPosition # Set the weight for Bezier Curve def setWeight(currentPosition, weightPosition, weight):   direction = weightPosition - currentPosition   direction *= weight   newWeightPosition = currentPosition + direction   return newWeightPosition if pointNum >= 3:  #create the new position list based on the original points  for i in range(0, pointNum):   #for the first point   if i == 0 :    #to find the position of the second position    currentPosition = points[i].position()    nextPosition = points[i+1].position()    thirdPosition = points[i+2].position()    secondPosition = getSecondPosition(currentPosition, nextPosition, thirdPosition)    #add the first and second point into the list    newPointList.append(currentPosition)    newPointList.append(secondPosition)   #for the last point   elif i == pointNum - 1:    #to find the position of the last second position    currentPosition = points[i].position()    nextPosition = points[i-1].position()    thirdPosition = points[i-2].position()    secondPosition = getSecondPosition(currentPosition, nextPosition, thirdPosition)    #add the first and second point into the list    newPointList.append(secondPosition)    newPointList.append(currentPosition)   #for the rest of points   else:    #find the center positions between the previous and next point    currentPosition = points[i].position()    previousPosition = points[i-1].position()    nextPosition = points[i+1].position()    previousCenterPosition = getCenterPosition(currentPosition, previousPosition)    nextCenterPosition = getCenterPosition(currentPosition, nextPosition)    #get the new center position based on the two center positions calculated above    newCenterPosition = getCenterPosition(previousCenterPosition, nextCenterPosition)    #get the displacement value and use it to push the two center positions out    #this method can make sure the Bezier Curve can pass through the original point positions    displacement = currentPosition - newCenterPosition    newPreviousCenterPosition = previousCenterPosition + displacement    newPreviousCenterPosition = setWeight(currentPosition, newPreviousCenterPosition, weight)    newNextCenterPosition = nextCenterPosition + displacement    newNextCenterPosition = setWeight(currentPosition, newNextCenterPosition, weight)    #add the new positions to the list    newPointList.append(newPreviousCenterPosition)    newPointList.append(currentPosition)    newPointList.append(newNextCenterPosition)  #clean the original points  geo.deletePoints(points)  #create the curve instance and sign the new positions to this curve one by one   curve = geo.createBezierCurve(len(newPointList))  for i in range(0, len(newPointList)):   vertex = curve.vertices()[i]   position = newPointList[i]   vertex.point().setPosition(position) if pointNum < 3:  geo.deletePoints(points) 

在实现了一条曲线的原型之后，把这个方法放到foreach里面循环一下就能够实现很多条曲线缠绕的效果了，注意的是原始点也不能够是贴在反弹几何体的表面的，最好把位置加上一点点法向量的矢量值。