多重线性回归分析的四大纪律三项注意
鉴于多重线性回归已经到了滥用的程度，特总结一下在使用线性回归时需要注意的问题，总结为四大纪律加三项注意。
四大纪律
四大纪律之一： 自变量与因变量之间要存在线性关系，可以通过绘制散点图矩阵来考察，若不符合，需要进行变量的变换予以修正。
四大纪律之二： 各个观测值y1/y2/y3......要相互独立，可通过残差图或durbin-watson检验予以考察。
四大纪律之三： 残差服从正态分布，可以通过标准化残差图考察
四大纪律之四： 方差齐性，也可以通过标准化残差考察
三项注意
三项注意之一： 样本量为自变量个数的5倍以上，要想效果好一些，最好20倍以上。
三项注意之二： 判断有误强影响点，如有应该改正数据或者剔除或采用稳健回归。
三项注意之三： 判断自变量之间有无强相关性，如有改用岭回归等方法。
例题说明：
某个公司计划在国内在开设几家分店，收集了目前分店的销售数据y以及分店所在城市的16岁以下人数x1,人均可支配收入x2,试进行分析（选自张文彤spss统计分析高级教程99页）
1.数据
两个自变量，21个样本含量，符合20倍原则
绘制散点图矩阵
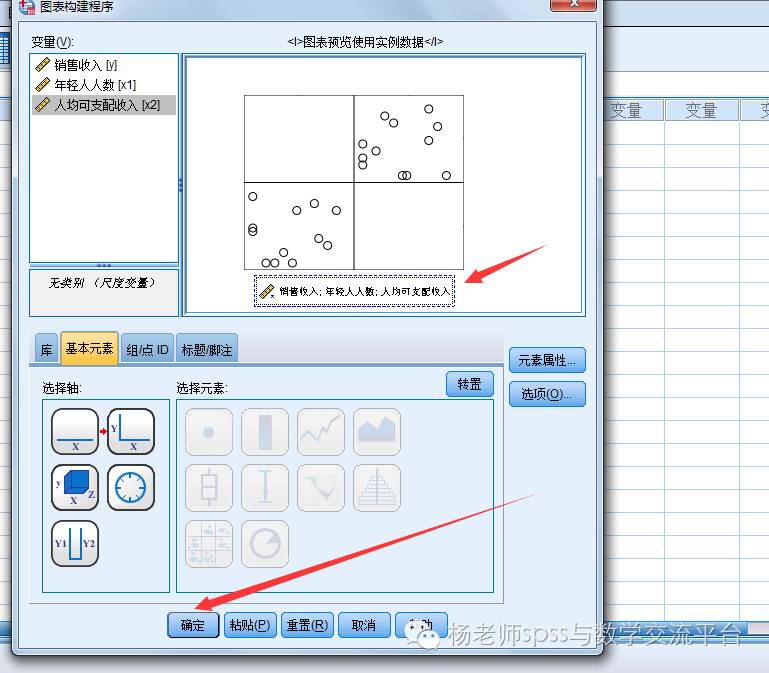
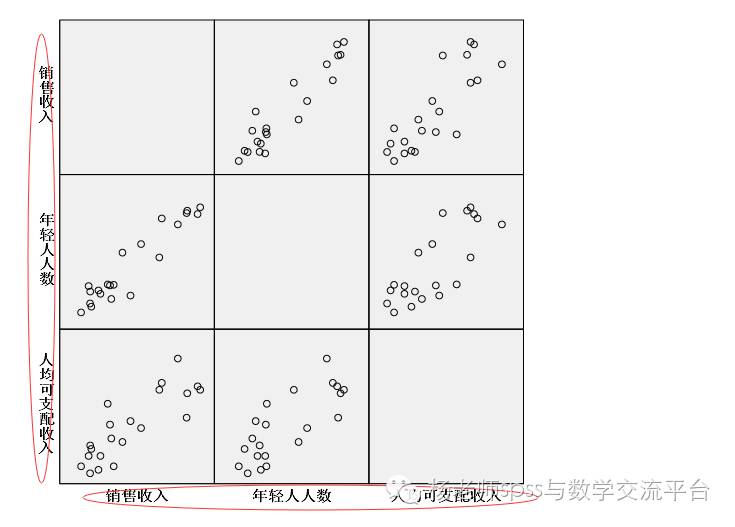
从图中可以看出，因变量与每个自变量都有线性关系
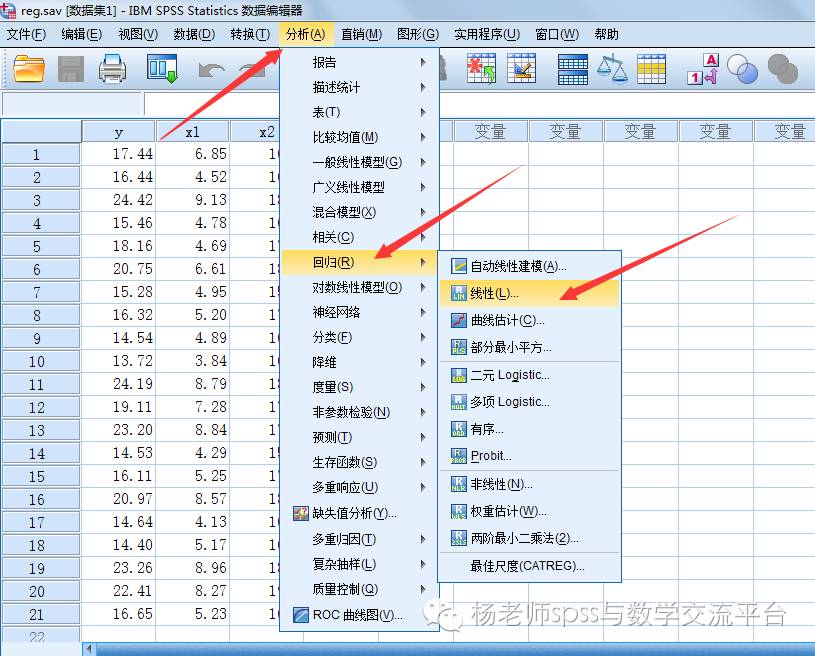
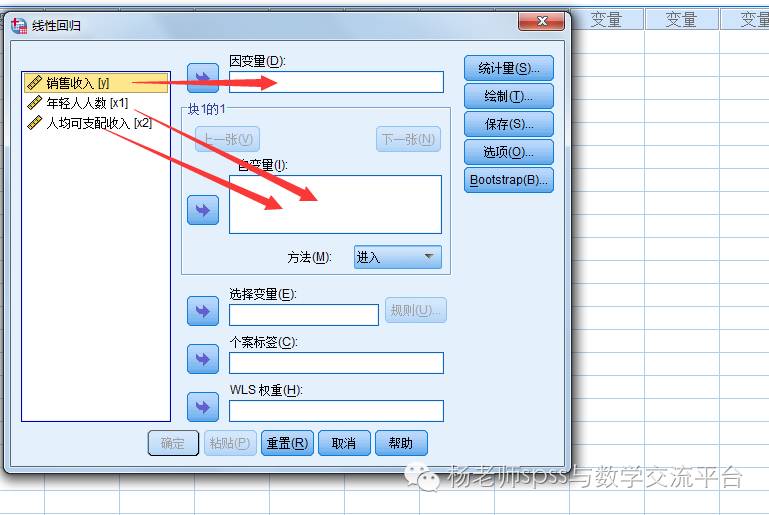
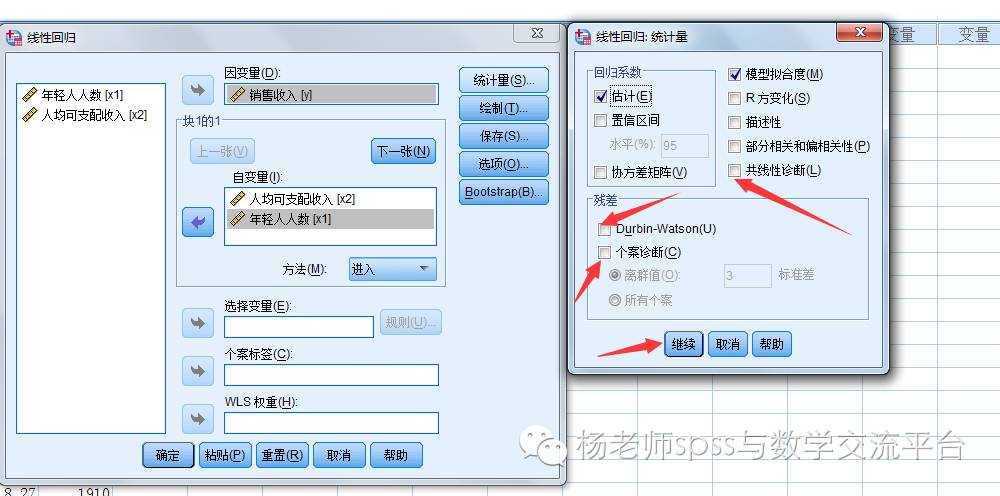
上图分别检查共线性，独立性和异常点
做残差图，横坐标为因变量，纵坐标为标准化残差
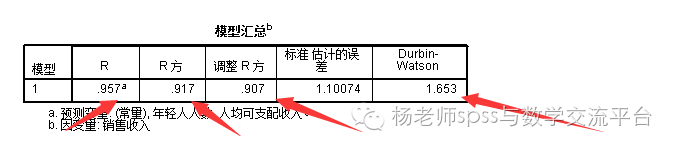
调整r的平方越近与1，回归效果越好，0.907效果不错，durbin watson值在2左右说明残差独立性较好。
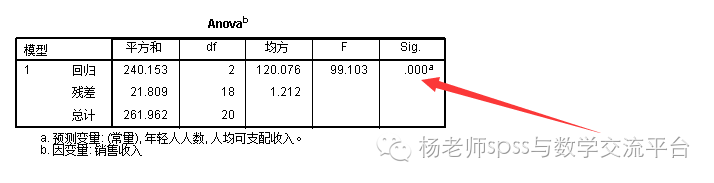
p=0.000小于0.05，线性回归为显著
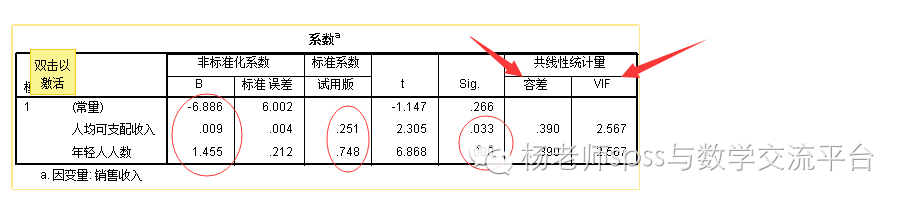
回归方程为y=-6.886+0.009人均支配收入+1.455人数，vif为方差膨胀因子一般只要不超过10，认为不存在共线性
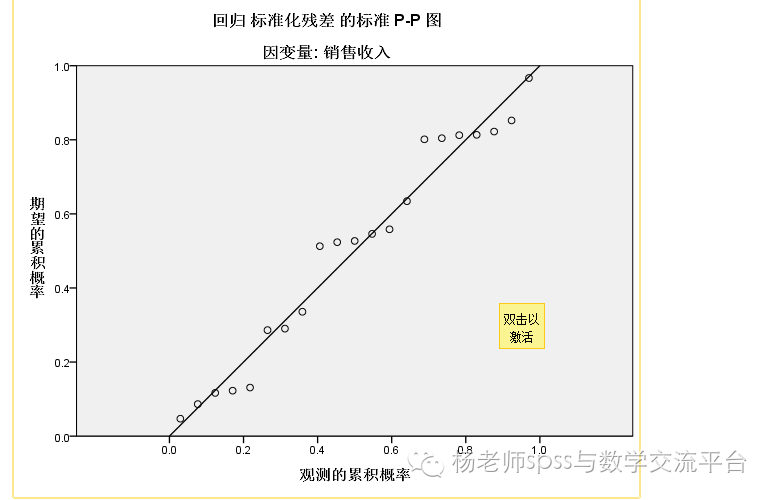
pp图，点在直线附近分布，近似一条直线，说明残差服从正态分布
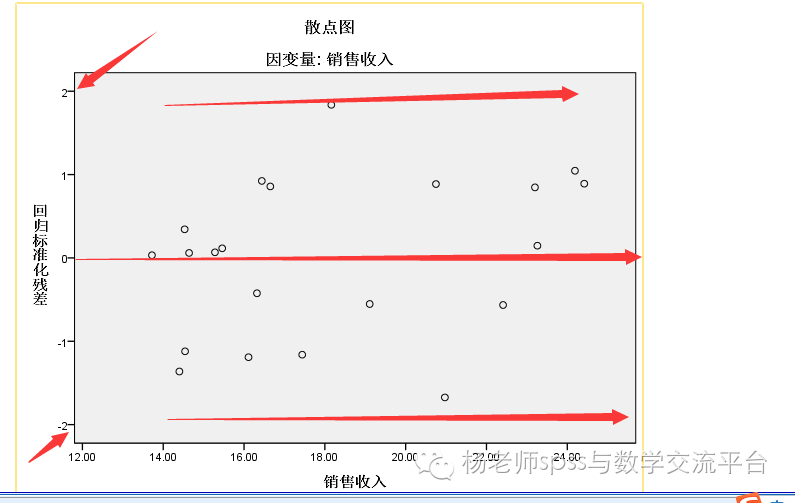
残差图，三点在零的附近均匀分布，而且没有超过正负3，认为残差服从正态分布且方差齐，且没有强影响点。
作者：杨老师
长按二维码关注该公众号，有数据分析问题加微信a42143917
正文到此结束
热门推荐
相关文章
近期评论
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
搞个gitee的项目
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
