转载

玩转中继器 | 九宫格拼图的实现原理

这个案例已经构思了很长时间，中间因为没有思路便放下了一段时间，前几天有朋友问我能否制作一个九宫格拼图的原型，于是又重新思考起来。这个原型最烧脑的地方就是图片移动逻辑的实现，因为只有空位周边的图片才可以将其移动到空位上。另外，这个原型有一个无解的BUG，为了实现图片的随机排列，导致了有时候生成的随机图片无法复原，也就是无论如何都拼不好，不过这种情况是随机出现的，有时候也是可以拼好的。

话说何为九宫格拼图？不说你已经懂了！

玩转中继器 | 九宫格拼图的实现原理

预览地址： http://raedme.cn/axurelab/010_jiugongpintu/

实现原理

好了，接下来就为大家解析一下这个拼图原型的实现原理（后文较为枯燥，阅读请谨慎）。

首先，是点击图片可以将图片移动到临近空白区域的原理。下面我借助一个模型来讲。

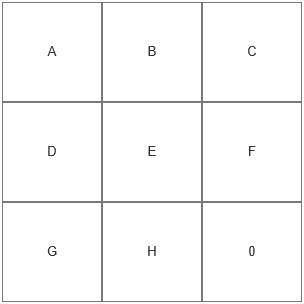
玩转中继器 | 九宫格拼图的实现原理

这是一个九宫格，在本案例中，九宫格我使用中继器来实现。九宫格中 A、B、C、D、E、F、G、H 分别代表八张图片，0 代表空白区域。此时，可以将图片 H 或者图片 F 移动到 0 位置，对应的 H 或 F 位置变成空白区域 0。之后再点击和 0 相邻的图片，遵循相同的移动原理。

那么问题来了，如何判断我点击的图片相邻位置有一个空白区域，可以将该图片移动到空白区域？此问题是该案例的核心问题，那么我接着用一个模型来给大家讲解。

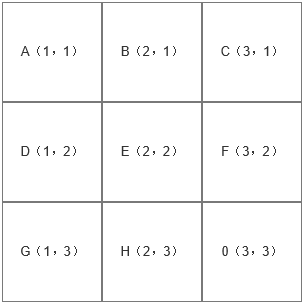
玩转中继器 | 九宫格拼图的实现原理

在这个图中，我为九宫格中的每个区域加一个坐标，用（x，y）来表示，这一步是实现该原型的关键步骤。然后我们来分析一下每个区域之间坐标的关系。

比如 F 区和 0 区之间的关系，H 区和 0 区之间的关系，其实就是空白区域和它相邻四周的区域的坐标关系。我们可以任意假设一个区域为空白区域，然后分析它上侧、下侧、左侧、右侧区域的（x，y）坐标。经过分析之后，我们可以得出一个结论。

可以用一个表达式来表达：

|0.x-相邻区域.x|+|0.y-相邻区域.y|=1

翻译一下就是：0 区域的 x 值减去相邻区域的 x 值的绝对值加上 0 区域的 y 值减去相邻区域的 y 值的绝对值等于 1。反过来推也成立，就是如果两个区域的（x，y）坐标分别求差的绝对值然后再相加等于 1 的话，那么这两个区域一定是相邻的区域。

通过以上逻辑，我们可以判断相邻区域（上下相邻 or 左右相邻），这非常重要。然后我们再判断一下相邻区域的其中一个是否为空白区域，如果是空白区域，那么点击另一个区域的时候，就可以将其移动到相邻的空白区域；如果不是空白区域，那么点击无效。

举例说明：

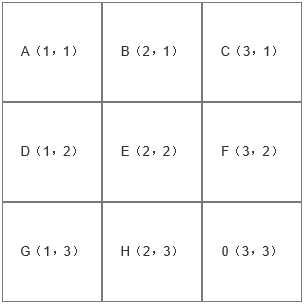
玩转中继器 | 九宫格拼图的实现原理

当我点击 H 区域的时候，首先要寻找它的相邻区域，通过前面介绍的表达式（|0.x-相邻区域.x|+|0.y-相邻区域.y|=1）我们可以得到 H 区域的相邻区域为 E、G、0（不要说你一看就知道，你一看就知道，但是中继器在运行的时候是不知道的，只能通过逻辑判断来获得）。

然后再判断这些相邻区域中是否有一个区域是空白区域，这个我们可以通过给中继器的数据集中加上一个标记字段来标记空白区域，这一步的实现较为简单。

这个例子中可以得知空白区域是 0 ，因此可以将 H 移动到 0 区域。

如果点击的区域是 E，那么其相邻的 4 个区域中就找不到空白区域，因此点击区域 E 就不会发生移动。

好了，基于以上逻辑，就可以实现九宫格拼图的核心功能了——点击图片移动到相邻的空白的区域，如果相邻没有空白区域，就不移动。

但是接下来还有另外一件事情就是，如何使拼图图片可以随机排列，并且每次原型载入时排列的顺序都不一样。

这一效果的实现我在以前的案例中都有讲过，可以通过给中继器的数据集增加一个排序字段，然后给排序字段赋值为随机数，之后为中继器增加排序。因为每次中继器数据集中的每行数据的排序字段的值都不一样，所以每次排序的结果会不一样。但是在本案例中需要考虑到要把空白区域始终排在最末尾，因此该数据项的排序字段需要做一个特殊的处理。

到这里九宫格拼图的主要实现逻辑就讲完了，不知道小伙伴们能否看得懂。具体的实现步骤，小伙伴们勇敢的去探索吧。

作者：大鹏，微信：urmagic，可一起交流原型设计问题，欢迎骚扰。

本文由 @大鹏原创发布于人人都是产品经理。未经许可，禁止转载。

原文 http://www.woshipm.com/rp/340913.html

正文到此结束