转载

如何简单形象地解释神经网络？

摘要：有网友在Quora上提问：对于那些非计算机科学行业的人，你会如何向他们解释机器学习和数据挖掘？斯坦福大学的印度学生、机器学习爱好者 PararthShah 在2012年12月22日的使用买芒果的例子，非常经典易懂。如何用类似的方法来解释神经网络？

0. 分类

神经网络最重要的用途是分类，为了让大家对分类有个直观的认识，咱们先看几个例子：

垃圾邮件识别：现在有一封电子邮件，把出现在里面的所有词汇提取出来，送进一个机器里，机器需要判断这封邮件是否是垃圾邮件。
疾病判断：病人到医院去做了一大堆肝功、尿检测验，把测验结果送进一个机器里，机器需要判断这个病人是否得病，得的什么病。
猫狗分类：有一大堆猫、狗照片，把每一张照片送进一个机器里，机器需要判断这幅照片里的东西是猫还是狗。

这种能自动对输入的东西进行分类的机器，就叫做分类器。

分类器的输入是一个数值向量，叫做特征（向量）。在第一个例子里，分类器的输入是一堆 0、1 值，表示字典里的每一个词是否在邮件中出现，比如向量 (1,1,0,0,0……) 就表示这封邮件里只出现了两个词 abandon 和 abnormal；第二个例子里，分类器的输入是一堆化验指标；第三个例子里，分类器的输入是照片，假如每一张照片都是 320*240 像素的红绿蓝三通道彩色照片，那么分类器的输入就是一个长度为 320*240*3=230400 的向量。

分类器的输出也是数值。第一个例子中，输出 1 表示邮件是垃圾邮件，输出 0 则说明邮件是正常邮件；第二个例子中，输出 0 表示健康，输出 1 表示有甲肝，输出 2 表示有乙肝，输出 3 表示有饼干等等；第三个例子中，输出 0 表示图片中是狗，输出 1 表示是猫。

分类器的目标就是让正确分类的比例尽可能高。一般我们需要首先收集一些样本，人为标记上正确分类结果，然后用这些标记好的数据训练分类器，训练好的分类器就可以在新来的特征向量上工作了。

1. 神经元

咱们假设分类器的输入是通过某种途径获得的两个值，输出是 0 和 1，比如分别代表猫和狗。现在有一些样本：

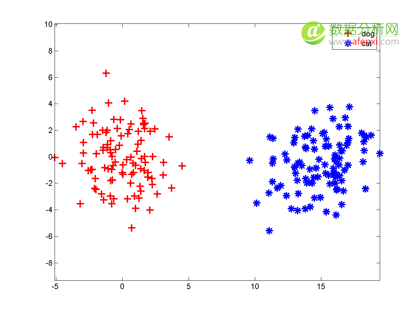
如何简单形象地解释神经网络？

大家想想，最简单地把这两组特征向量分开的方法是啥？当然是在两组数据中间画一条竖直线，直线左边是狗，右边是猫，分类器就完成了。以后来了新的向量，凡是落在直线左边的都是狗，落在右边的都是猫。

一条直线把平面一分为二，一个平面把三维空间一分为二，一个 n-1 维超平面把 n 维空间一分为二，两边分属不同的两类，这种分类器就叫做神经元。

大家都知道平面上的直线方程是

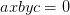
如何简单形象地解释神经网络？

，等式左边大于零和小于零分别表示点

如何简单形象地解释神经网络？

在直线的一侧还是另一侧，把这个式子推广到 n 维空间里，直线的高维形式称为超平面，它的方程是：

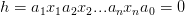
如何简单形象地解释神经网络？

神经元就是当 h 大于 0 时输出 1，h 小于 0 时输出 0 这么一个模型，它的实质就是把特征空间一切两半，认为两瓣分别属两个类。你恐怕再也想不到比这更简单的分类器了，它是 McCulloch 和 Pitts 在 1943 年想出来了。

这个模型有点像人脑中的神经元：从多个感受器接受电信号

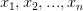
如何简单形象地解释神经网络？

，进行处理（加权相加再偏移一点，即判断输入是否在某条直线

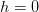
的一侧），发出电信号（在正确的那侧发出 1，否则不发信号，可以认为是发出 0），这就是它叫神经元的原因。

当然，上面那幅图我们是开了上帝视角才知道“一条竖直线能分开两类”，在实际训练神经元时，我们并不知道特征是怎么抱团的。神经元模型的一种学习方法称为 Hebb 算法：

先随机选一条直线 / 平面 / 超平面，然后把样本一个个拿过来，如果这条直线分错了，说明这个点分错边了，就稍微把直线移动一点，让它靠近这个样本，争取跨过这个样本，让它跑到直线正确的一侧；如果直线分对了，它就暂时停下不动。因此训练神经元的过程就是这条直线不断在跳舞，最终跳到两个类之间的竖直线位置。

2. 神经网络

MP 神经元有几个显著缺点。首先它把直线一侧变为 0，另一侧变为 1，这东西不可微，不利于数学分析。人们用一个和 0-1 阶跃函数类似但是更平滑的函数 Sigmoid 函数来代替它（Sigmoid 函数自带一个尺度参数，可以控制神经元对离超平面距离不同的点的响应，这里忽略它），从此神经网络的训练就可以用梯度下降法来构造了，这就是有名的反向传播算法。

神经元的另一个缺点是：它只能切一刀！你给我说说一刀怎么能把下面这两类分开吧。

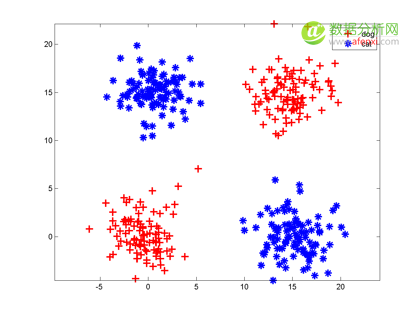
如何简单形象地解释神经网络？

解决办法是多层神经网络，底层神经元的输出是高层神经元的输入。我们可以在中间横着砍一刀，竖着砍一刀，然后把左上和右下的部分合在一起，与右上的左下部分分开；也可以围着左上角的边沿砍 10 刀把这一部分先挖出来，然后和右下角合并。

每砍一刀，其实就是使用了一个神经元，把不同砍下的半平面做交、并等运算，就是把这些神经元的输出当作输入，后面再连接一个神经元。这个例子中特征的形状称为异或，这种情况一个神经元搞不定，但是两层神经元就能正确对其进行分类。

只要你能砍足够多刀，把结果拼在一起，什么奇怪形状的边界神经网络都能够表示，所以说神经网络在理论上可以表示很复杂的函数 / 空间分布。但是真实的神经网络是否能摆动到正确的位置还要看网络初始值设置、样本容量和分布。

神经网络神奇的地方在于它的每一个组件非常简单——把空间切一刀 + 某种激活函数 (0-1 阶跃、sigmoid、max-pooling)，但是可以一层一层级联。输入向量连到许多神经元上，这些神经元的输出又连到一堆神经元上，这一过程可以重复很多次。这和人脑中的神经元很相似：每一个神经元都有一些神经元作为其输入，又是另一些神经元的输入，数值向量就像是电信号，在不同神经元之间传导，每一个神经元只有满足了某种条件才会发射信号到下一层神经元。当然，人脑比神经网络模型复杂很多：人工神经网络一般不存在环状结构；人脑神经元的电信号不仅有强弱，还有时间缓急之分，就像莫尔斯电码，在人工神经网络里没有这种复杂的信号模式。

如何简单形象地解释神经网络？

神经网络的训练依靠反向传播算法：最开始输入层输入特征向量，网络层层计算获得输出，输出层发现输出和正确的类号不一样，这时它就让最后一层神经元进行参数调整，最后一层神经元不仅自己调整参数，还会勒令连接它的倒数第二层神经元调整，层层往回退着调整。这很像中国的文艺体制，武媚娘传奇剧组就是网络中的一个神经元，最近刚刚调整了参数。

3. 大型神经网络

我们不禁要想了，假如我们的这个网络有 10 层神经元，第 8 层第 2015 个神经元，它有什么含义呢？我们知道它把第七层的一大堆神经元的输出作为输入，第七层的神经元又是以第六层的一大堆神经元做为输入，那么这个特殊第八层的神经元，它会不会代表了某种抽象的概念？

就好比你的大脑里有一大堆负责处理声音、视觉、触觉信号的神经元，它们对于不同的信息会发出不同的信号，那么会不会有这么一个神经元（或者神经元小集团），它收集这些信号，分析其是否符合某个抽象的概念，和其他负责更具体和更抽象概念的神经元进行交互。

2012 年多伦多大学的 Krizhevsky 等人构造了一个超大型卷积神经网络 [1]，有 9 层，共 65 万个神经元，6 千万个参数。网络的输入是图片，输出是 1000 个类，比如小虫、美洲豹、救生船等等。这个模型的训练需要海量图片，它的分类准确率也完爆先前所有分类器。纽约大学的 Zeiler和Fergusi [2]把这个网络中某些神经元挑出来，把在其上响应特别大的那些输入图像放在一起，看它们有什么共同点。他们发现中间层的神经元响应了某些十分抽象的特征。

第一层神经元主要负责识别颜色和简单纹理：

如何简单形象地解释神经网络？

第二层的一些神经元可以识别更加细化的纹理，比如布纹、刻度、叶纹。

如何简单形象地解释神经网络？

第三层的一些神经元负责感受黑夜里的黄色烛光、鸡蛋黄、高光。

如何简单形象地解释神经网络？

第四层的一些神经元负责识别萌狗的脸、七星瓢虫和一堆圆形物体的存在。

如何简单形象地解释神经网络？

第五层的一些神经元可以识别出花、圆形屋顶、键盘、鸟、黑眼圈动物。

如何简单形象地解释神经网络？

这里面的概念并不是整个网络的输出，是网络中间层神经元的偏好，它们为后面的神经元服务。虽然每一个神经元都傻不拉几的（只会切一刀），但是 65 万个神经元能学到的东西还真是深邃呢。

[1] Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems (pp. 1097-1105).

[2] Zeiler, M. D., & Fergus, R. (2013). Visualizing and understanding convolutional neural networks. arXiv preprint arXiv:1311.2901.

来源：知乎

作者：王小龙

链接：https://www.zhihu.com/question/22553761

原文 http://www.itongji.cn/cms/article/articledetails?articleid=2105

正文到此结束