欧拉计划 : 557. 划分三角形
题目
Problem 557. Cutting triangles
A triangle is cut into four pieces by two straight lines, each starting at one vertex and ending on the opposite edge. This results in forming three smaller triangular pieces, and one quadrilateral. If the original triangle has an integral area, it is often possible to choose cuts such that all of the four pieces also have integral area. For example, the diagram below shows a triangle of area 55 that has been cut in this way.
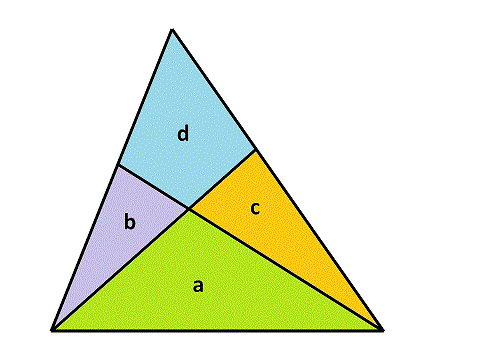
Representing the areas as a, b, c and d, in the example above, the individual areas are a = 22, b = 8, c = 11 and d = 14. It is also possible to cut a triangle of area 55 such that a = 20, b = 2, c = 24, d = 9.
Define a triangle cutting quadruple (a, b, c, d) as a valid integral division of a triangle, where a is the area of the triangle between the two cut vertices, d is the area of the quadrilateral and b and c are the areas of the two other triangles, with the restriction that b ≤ c. The two solutions described above are (22,8,11,14) and (20,2,24,9). These are the only two possible quadruples that have a total area of 55.
Define S(n) as the sum of the area of the uncut triangles represented by all valid quadruples with a+b+c+d ≤ n.For example, S(20) = 259.
Find S(10000).
分析
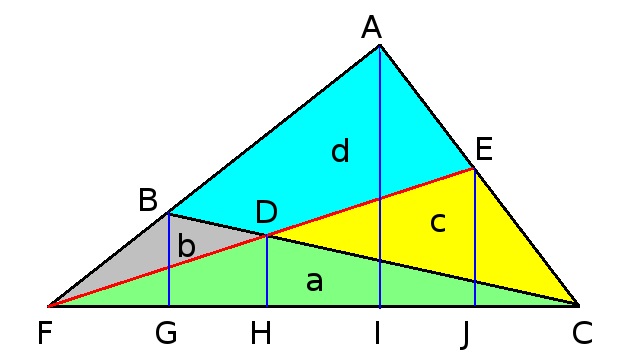
如上图, 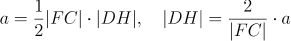 ,令
,令 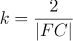 ,则:
,则:
其中 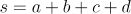 。由 梅涅劳斯定理 ,我们有:
。由 梅涅劳斯定理 ,我们有:
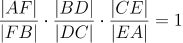
根据相似三角形的性质,我们有:
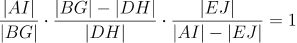
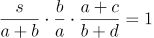
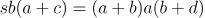

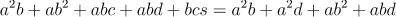
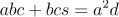
最终得到:

由于这些变量都是整数,我们可以枚举 s, a, d,尝试解出 b, c 。
解答
根据以上分析,我们有以下 Haskell 程序:
import Math.NumberTheory.Powers.Squares ( isSquare ) main = let n = 10^4 in print $ sum [s | s <- [4..n], a <- [1..s-3], let e=a*a; f=s+a; t = div f $ gcd e f, d <- [t,t+t..s-a-2], let g = s-a-d, isSquare $ g*g - 4 * (div (d*e) f)] 简要说明:
- 第1层循环:量
s从4递增到n。 - 第2层循环:量
a从1递增到s-3。 - 第3层循环:量
d从t递增到s-a-2,步长为t。 - 量
t等于 。
。 - 量
g等于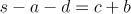 。
。 - 量
div (d*e) f等于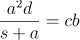 。
。 - 量
g*g - 4 * (div (d*e) f)等于 。
。
这个程序的运行时间是 86 秒,不符合欧拉计划的一分钟原则。
优化
上述程序的最内层的 d 循环不必进行到底:

简要说明:
- 第5行的
takeWhile函数用于提前终止最内层的d循环。 -
isSquare'函数不检查自变量是否小于零,从而稍微加快速度。
这个程序的运行时间是 41 秒。
参考资料
- Wikipedia: Menelaus' theorem
- Wikipedia: Similarity (geometry)
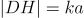













![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

