转载

强化学习系列之七:逆向强化学习 | AlgorithmDog

这篇文章我们介绍逆向强化学习 (Inverse Reinforcement Learning)。

1. 逆向强化学习是什么

我们知道强化学习背后的假设是马尔科夫决策过程 (MDP)。马尔可夫决策过程是基于马尔可夫过程理论的随机动态系统的决策过程，其分五个部分：

1. /(S/)

$S$ 状态集 (states)；
2. /(A/) $A$ 动作集 (Action)；
3. /(P_{s,a}^{s'}/) $P_{s,a}^{s'}$ 转移概率；
4. /(R_{s}/) $R_{s}$ 或者 /(R_{s,a}/) $R_{s,a}$ 奖励函数；
5. /(/gamma/) $/gamma$ 衰减因子。

有时候我们不知道转移概率和激励函数，便让系统探索环境。在探索过程中，环境根据我们未知的转移概率和激励函数，确定下一个状态和给出激励。这一类强化学习被称为模型无关的强化学习。逆向强化学习更极端：系统进行探索的过程中，环境不给出奖励。一般的强化学习的训练数据是 /(/{s_1,a_1,r_1,...,s_n,a_n,r_n/}/)

$/{s_1,a_1,r_1,...,s_n,a_n,r_n/}$ ，而逆向强化学习的训练数据是一组轨迹 /(/{/zeta = s_1,a_1,...,s_n,a_n/}/) $/{/zeta = s_1,a_1,...,s_n,a_n/}$ 。

为什么人们要发明逆向强化学习呢？说一个场景，训练自动导航机器人，我们拿到的出租车司机的行为数据是一组轨迹 /(/{/zeta = s_1,a_1,...,s_n,a_n/}/)

$/{/zeta = s_1,a_1,...,s_n,a_n/}$ ，我们无法获得司机在一个地址做了一个动作的即时奖励。可以用有监督学习处理这个问题，分类器的输入是地点，输出是动作。这种方法被称为行为克隆 (Behavior Cloning)。行为克隆有两个缺陷。一个是导航本质上是强化学习的范畴。导航行为的优劣是有整体用时决定的，整体用时只有在最后才知道，具有强化学习教师信号延迟特点。另一个是行为克隆只学习司机的行为，并没有深究司机的动机。

逆向强化学习的马尔科夫决策过程不知道奖励函数，但是有教师策略探索环境的结果。

1. /(S/)

$S$ 表示状态集 (states)；
2. /(A/) $A$ 表示动作集 (Action)；
3. /(P_{s,a}^{s'}/) $P_{s,a}^{s'}$ 表示状态 s 下采取动作 a 之后转移到 s' 状态的概率；
4. /(D = /{/zeta = s_1,a_1,...,s_n,a_n /}/) $D = /{/zeta = s_1,a_1,...,s_n,a_n /}$ 表示教授策略探索环境的轨迹；
5. /(/gamma/) $/gamma$ 是衰减因子。

2. 逆向强化学习算法

逆向强化学习算法的目标是还原激励函数 /(R_{s}^{*}/)

$R_{s}^{*}$ 。一个重要假设是奖励函数等于状态特征向量和参数向量内积
/begin{eqnarray}
R_{s} = /pmb{/theta}^T/pmb{/phi(s)} /nonumber
/end{eqnarray}
其中 /(/pmb{/theta} /in R^n/) $/pmb{/theta} /in R^n$ 是参数向量， /(/phi(s): s /rightarrow R^n/) $/phi(s): s /rightarrow R^n$ 将状态 s 映射到状态特征向量。只要求得参数 /(/pmb{/theta}/) $/pmb{/theta}$ ，即得奖励函数。逆向强化学习的目标是使得下面的公式成立。
/begin{eqnarray}
E[/sum_{t=0}^{/infty}/gamma^{t}R_{s_t}^{*}|/pi^{*}] &/ge& E[/sum_{t=0}^{/infty}/gamma^{t}R_{s_t}^{*}|/pi] /quad /forall /pi /nonumber //
/Rightarrow /pmb{/theta}E[/sum_{t=0}^{/infty}/gamma^{t}/phi(s_t)|/pi^{*}] &/ge& /pmb{/theta}E[/sum_{t=0}^{/infty}/gamma^{t}/phi(s_t)|/pi] /quad /forall /pi /nonumber //
/Rightarrow /pmb{/theta}u(/pi^{*}) &/ge& /pmb{/theta}u(/pi) /quad /forall /pi /nonumber //
/end{eqnarray}
其中 /(u(/pi)/) $u(/pi)$ 表示策略 /(/pi/) $/pi$ 下的状态特征的期望。本来 /(/pi^{*}/) $/pi^{*}$ 表示最优策略。但我们对最优策略长什么样完全没有头绪，故而假设教师策略就是最优策略 /(/pi^{*}/) $/pi^{*}$ 。我们介绍两种逆向强化学习的算法。

2.1 学徒学习

Abbeel and Ng, 2004 提出了学徒学习解决逆向强化学习问题。学徒先观察自己方法和师傅的差距并猜测原因，根据猜测结果尝试改进自己方法，再观察自己方法和师傅的差距并猜测原因，循环往复，直到自己和师傅差不多。因此学徒学习有两个步骤：

猜测步骤，观察已有策略和教师策略的差距，并猜测奖励函数。猜测步骤的目标得到奖励函数参数，优化问题如下所示。
/begin{eqnarray}
max.& &/gamma /nonumber //
st. & &/theta^T u(/pi^*) /ge /theta^T u(/pi_i) + /gamma, i /in /{1,...n-1/} /nonumber //
st. & &||/theta||_w<1 /nonumber /end{eqnarray} 猜测步骤的代码 (建议先简单学习下线性规划包 pulp 的用法 )：

def guess_reward(self, policys):     gamma = LpVariable("gamma");     theta = [];     for i in xrange(len(self.theta)):         theta.append(LpVariable("theta_%d"%(i), -1.0,1.0));      prob = LpProblem("guess_reward", LpMaximize);     e = 0     for i in xrange(len(self.theta)):         e += theta[i]     prob += e < 1     prob += e > -1      for p in policys:         e = 0         for u in xrange(len(self.trajectories_u)):             e += theta[u] * self.trajectories_u[u]             e -= theta[u] * p.u[u]         e -= gamma         prob += e >= 0     prob += gamma;              prob.solve()     for i in xrange(len(self.theta)):         self.theta[i] = value(theta[i])

学习步骤根据猜测的奖励函数，学习一个新策略。我们使用奖励函数参数得到教师策略轨迹的奖励，再利用蒙特卡罗方法学习一个新策略。

def learn_policy(self, trajectories):      policy = Apprenticeship_Policy(self.mdp);     n      = dict();     for s_a in policy.q:         n[s_a]        = 0.0001;         policy.q[s_a] = 0.0;      for t in trajectories:         G = 0.0;            for i in xrange(len(t.states)-1,0,-1):             s  = t.states[i];             r  = self.state_reward(mdp.feas[s]);             G *= self.mdp.gamma;              G += r;          for i in xrange(len(t.states)-1):             s  = t.states[i];             a  = t.actions[i];             policy.q["%s_%s"%(s,a)] += G;             n["%s_%s"%(s,a)]        += 1.0;             G -= self.state_reward(mdp.feas[s]);             G /= self.mdp.gamma;                                 for s_a in policy.q:         if n[s_a] > 0.1:  policy.q[s_a] /= n[s_a];     return policy

3. 做个实验

实验还是以机器人找金币为场景。机器人从任意一个状态出发寻找金币，找到金币则获得奖励 1，碰到海盗则损失 1。找到金币或者碰到海盗，机器人都停止。衰减因子 /(/gamma/)

$/gamma$ 设为 0.8。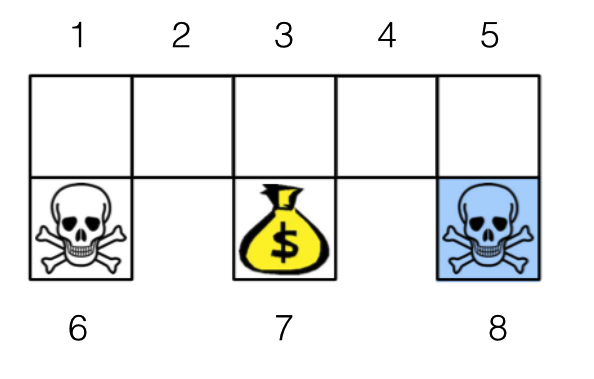

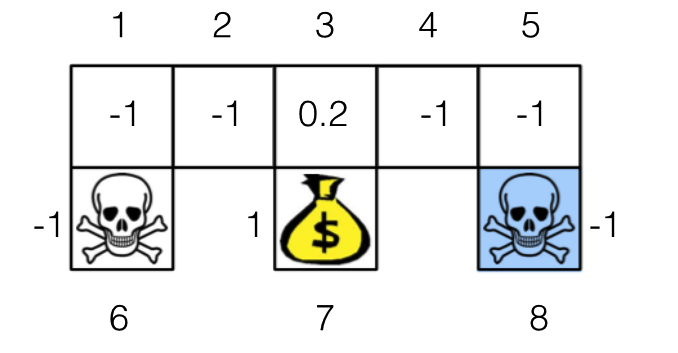
我们用学徒学习得到的奖励函数如下图所示 ( 实验代码 )。我们很容易知道，这个奖励函数和机器人找金币的奖励函数，导致的最优策略是一样的。

4. 总结

本文介绍了逆向强化学习中的学徒学习。下次将更新本文，添加其他逆向强化学习算法。本文代码可以在 Github 上找到，欢迎有兴趣的同学帮我挑挑毛病。

最后欢迎关注我的公众号 AlgorithmDog，每周日的更新就会有提醒哦~

参考文献

Abbeel P, Ng A Y. Apprenticeship learning via inverse reinforcement learning[C]//Proceedings of the twenty-first international conference on Machine learning. ACM, 2004: 1.