翻译：深入理解 Clojure Persistent Vectors 实现 Part 2

前言

• 原文地址： http://hypirion.com/musings/understanding-persistent-vector-pt-2
• 上一篇： 翻译:深入理解 Clojure Persistent Vectors 实现 Part 1

正文

在前一篇关于 Clojure Persistent Vectors 的博客里（ 如果你还没有读过，请点击阅读 ），我们大致理解了 vector 里元素的插入、更新和出队操作是如何工作的。我们还没有真正了解到是如何定位到正确的元素，在这篇博客我将介绍查找元素是如何实现的。

为了理解我们是如何在树的节点里面选择正确的分支，我想最好是先给这些结构一个合适的名称，并解释 为什么 这样命名。通过一个数据结构的名称来解释分支选择似乎听起来很奇怪，但是如果考虑到这个名称可能描述了它的工作原理的话，这还是有意义的。

名称

Clojure persistent vector 数据结构的一个更正式的名称是 持久的按位分区的矢量前缀树( persistent bit-partitioned vector trie ) 。我在前篇博客介绍的其实是持久的按数字分区的前缀树(persistent digit-partitioned vector tries)是如何运行的，但是不用担心，一个按位分区前缀树只是一个按数字分区的前缀树的优化，对于上篇博客的内容来说，两者并没有区别。在本篇博客，会介绍一点两者在性能上的小区别。否则它们其实没有根本上的差异。

我猜测你可能并不了解上面段落提到的这些术语，所以我将在下文一一解释。

持久性

在上一篇博客，我使用了术语持久性（persistent）。我说我们想要数据结构是持久的，但是并没有真正解释到底持久性本身意味着什么。

一个称为持久的数据结构并不修改它自己本身：严格来讲，他们并不一定要在内部是不可变的，只是需要被（外界）认为是不可变的。无论何时你在一个持久的数据结构上执行了更新、插入或者删除操作，一个新的数据结构将返回给你。老的版本仍然是一致的，并且无论什么时候你给它一个输入，它总是返回同样的输出（译者注：也就是没有副作用，side effects）。

当我们谈论一个 完全 持久的数据结构的时候，这个数据结构的任何版本都是可以修改的，意思是作用在某个版本上的所有可能的操作，都可以作用在另一个版本上。在早期的『函数式数据结构』时代，更常见的方式是和数据结构一起『欺骗』，通过修改内部结构让老的版本随着时间逐渐『腐朽』，同时跟最新版本相比是越来越慢。虽然如此，Rich Hickey（译者注：Clojure 作者）决定让 Clojure 持久数据结构的所有版本都有一样的性能承诺，无论你正在使用的是数据结构的哪个版本。

矢量(Vector)

一个矢量就是一个一维的可增长的数组。例如 C++ 的 std::vector 或者 Java 的 java.util.ArrayList 就是可变矢量的实现。实际上也没有比这个更多的解释了。一个矢量前缀树是指一棵用来表示矢量的前缀树(trie)。它并不一定必须是持久的，但是在我们这里介绍的是持久的。

前缀树（Trie)

前缀树是特殊的一种树，我想最好先解释更多的常见的树来展示前缀树的实际不同之处。

在红黑树和其他类型的二叉树里，映射或者元素存在于内部的节点上。 选择正确的分支是通过比较元素/关键字(key)和当前节点来确定的 ：如果元素比当前节点的元素小，那么我们选择左分支，如果更大，我们就走到右分支。叶子节点通常都是空指针或者 nil，不包含任何东西。

“Example red-black tree” by Cburnett , CC-BY-SA 3.0

上面图中的红黑树是从维基百科的文章里摘录过来的。我并不想详细介绍它是如何运作的的，但是我们选择一个小小的例子，看看我们是如何判断 22 是否在这棵红黑树里：

1. 我们从根节点 13 开始，和 22 对比下。因为 13 < 22，所以我们进入 右 分支。
2. 新节点包含了 17，和 22 对比。因为 17 < 22，我们仍然进入 右 分支。
3. 下一个我们进入的节点是 25。因为 25 > 22，我们进入 左 分支。
4. 下一个节点是 22，因此我们知道 22 包含在这棵树里。

如果你想知道关于红黑树的更好的解释，我推荐你阅读 Julienne Walker 的 红黑树教程 。

从另一方面观察，一棵前缀树将它的所有的值都保存在它的叶子节点中。 选择正确的分支是通过使用关键字的一部分来定位 。因此，一棵前缀树可以有多于两个的分支，在我们这里，它最多拥有 32 个分支！

大致的一棵前缀树插图展示在上面图中。它展示的前缀树是一个 map：接收长度为 2 的字符串，当字符串在前缀树里存在的时候返回一个整数。 ac 的值是 7，而 ba 的值是 8。前缀树是这么工作的：

对于字符串，我们把字符串拆成字符。然后使用第一个字符，找到表示该值的边(edge)，然后沿着边往下走。如果该值没有找到对应的边(edge)，我们就停止访问，表示它在前缀树里不存在。否则，我们继续使用第二个字符来查找边，不停下去直到没有剩余字符了。最终完成的时候，如果存在，我们就返回当前的值。

以 ac 字符串为例，我们按照下列步骤处理：

1. 把 ac 拆成成 [a, c] 的字符列表，并从前缀树的根节点开始。
2. 判断对于字符 a ，节点上有没有一条边，如果存在，我们沿着这条边向下访问。
3. 判断对于字符 c ，节点上有没有一条边，如果存在，我们同样沿着这条边向下访问。
4. 后面没有剩余的字符了，这就是意味着当前节点包含了值 7，因此我们返回 7。

Clojure 的 Persistent Vector 就是一棵前缀树，它把元素的索引位置(index)作为关键字(key)使用。但是，正如你所料到的那样，我们需要将索引整数按照某种方式拆分。为了拆分整数，我们要么使用 数字分区 的方式，或者它的更快版本—— 位分区 。

数字分区（Digit partitioning）

数字分区的意思是说我们把关键字拆分成数字，作为填充前缀树的基础。例如，我们可以将关键字 9128 拆分成 [9, 1, 2, 8] ，基于这个列表将元素放入前缀树中。如果前缀树的深度超过了这个数字列表的大小，我们可能还需要在列表前面填充一些 0。

我们也可以使用任何其他我们喜欢的基数，不仅仅是 10。这样一来，我们就需要将关键字转换成想要使用的基数，并使用转换后的数字。仍然以 9128 为例， 9128 换算成基数为 7 的数字就是 35420 ，接下来我们就要使用列表 [3, 5, 4, 2, 0] 来查找或者插入前缀树。

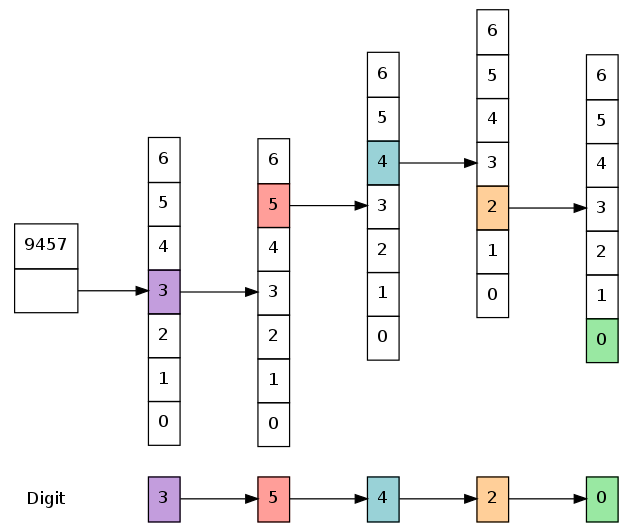
上面这棵前缀树（横向展开，不包含我们不会访问的边和节点）展示了我们如何遍历一棵数字分区的前缀树：我们挑选了最高位有效的数字，在这里是 3，然后进入那个指定的分支。接着以同样的方式使用第二高位有效的数字，一直到没有剩余的数字为止。当我们访问到最后分支的时候，和我们在一起的对象 —— 这里就是最后数组的的第一个对象（译者注：绿色的 0） —— 就是我们想要定位的对象。

如果你知道怎么找到数字，那么实现这样一种查找程序并不很难。下面是一个 Java 版本的实现，与查找无关的细节都被剥离掉了：

public class DigitTrie {   public static final int RADIX = 7;    // Array of objects. Can itself contain an array of objects.   Object[] root;   // The maximal size/length of a child node (1 if leaf node)   int rDepth; // equivalent to RADIX ** (depth - 1)    public Object lookup(int key) {     Object[] node = this.root;      // perform branching on internal nodes here     for (int size = this.rDepth; size > 1; size /= RADIX) {       node = (Object[]) node[(key / size) % RADIX];       // If node may not exist, check if it is null here     }      // Last element is the value we want to lookup, return it.     return node[key % RADIX];   } } 

rDepth 的值表示根节点的一个子节点的最大大小：一个有 n 个数字组成的数字，将拥有 RADIX 的 n 次幂数量的可能值，而且我们必须能将它们毫无冲突地全部放入前缀树。

在 lookup 方法的 for 循环里， size 的值表示当前节点的一个子节点的可以拥有的最大大小。对于每个我们访问过的子节点，这个 size 大小被分支因子递减，分支因子即是数字前缀树的基数。

对结果做一次取模运算的原因是为了忽略掉高位有效数字 —— 那些我们在前面用于分支选择的数字。我们可以在每次分支选择进入子节点的时候从关键字里移除高位数字，但是在那种情况下，代码会变得稍微复杂一点。

位分区

数字分区的前缀树通常需要做大量的整数除法和取模运算。在每次分支选择的时候必须执行这些运算会带来不少的时间损耗。如果可能，我们当然更想要加快这一部分的运算。

因此，正如你所料，位分区前缀树是数字分区前缀树的一个子集。所有基于 2 的次幂（2, 4, 8, 16, 32 等）为基数的数字分区前缀树，都可以转成位分区前缀树。只要了解一些位运算的知识，我们就能移除这些耗时的算术运算。

从概念上讲，它的工作原理跟数字分区是一样的。尽管如此，我们原来把关键字拆分为数字，现在替换成拆分为预定义大小的位簇(bit chunk)。对于 32-路的分叉前缀树来说，每一部分都需要 5 位，对于 4-路的分叉前缀树来说，每一位簇需要 2 位。更一般的说法，我们需要的是和我们的指数大小一样的位数（译者注：举例来说，32 是 2 的 5 次幂，5 是指数，因此是 5 位）。

但是，这样做为什么更快呢？通过使用一些位运算的技巧，我们可以同时消除整数的除法和取模。如果 power 是 2 的 n 次幂，我们可以得到 x / power == x >>> n 和 x % power == x & (power - 1) 。这两个公式其实是等价，跟整数的本质表示有关，也就是位组成的序列。

如果我们使用这个结果，并和前面的实现组合起来，我们将得到下列代码：

public class BitTrie {   public static final int BITS = 5,                           WIDTH = 1 << BITS, // 2^5 = 32                           MASK = WIDTH - 1; // 31, or 0x1f    // Array of objects. Can itself contain an array of objects.   Object[] root;   // BITS times (the depth of this trie minus one).   int shift;    public Object lookup(int key) {     Object[] node = this.root;      // perform branching on internal nodes here     for (int level = this.shift; level > 0; level -= BITS) {       node = (Object[]) node[(key >>> level) & MASK];       // If node may not exist, check if it is null here     }      // Last element is the value we want to lookup, return it.     return node[key & MASK];   } } 

这近似于 Clojure 语言的实现。看 Clojure 语言里的 这些代码 来检验这一点。唯一的区别是它做了边界检查以及末尾检查。

需要重点注意的是在这里我们不仅改变了运算符，而且还把 rDepth 值替换成了 shift 值。不再是存储完全的值，而只是存储指数部分。这使得我们可以对关键字使用位移运算，也就是 (key >>> level) 这一段。如果你相当熟悉位运算，其他部分也都很直白，容易理解。虽然这样，我们还是为不熟悉这些技巧的朋友举个例子。下面这个解释很详细，如果你觉的自己已经理解了，可以忽略。

为了图形化展示，假设我们只有 2 位分区（4-路分叉），而不是 5 位（32-路分叉）。如果我们想在一棵拥有 887 个元素的前缀树里查找某个值，我们有 shift 值等于 8：根节点的所有子节点每个最多可以包含 1 << 8 == 256 个元素。宽度(width)和掩码(mask)也都同时被改变：掩码 mask 是 3，而不是原来的 31。

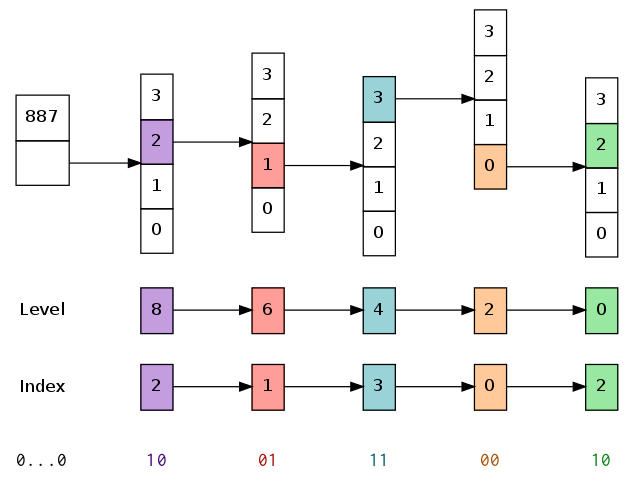
假设我们想查找的关键字 626 对应的内容， 626 的二进制表示是 0000 0010 0111 0010 。按照上面或者 Clojure 语言里编写的算法，一步一步介绍，我们会按照下列步骤处理：

• node 被设置为根节点，而 level 设置为 8。
• 因为 level 大于 0，我们开始进入 for 循环。
  • 我们先执行运算 key >>> level ，在这里就是 636 >>> 8 ，这将消去前面（低位）的 8 位，剩下来是 0000 0010 ，也就是十进制的数字 2。
  • 接下来计算掩码 (key >>> level) & MASK == 2 & 3 。掩码将前两位之外的位都设置为 0。这里的结果没有区别，结果仍然是 2。
  • 我们将当前节点 node 设置为它在位置 2 的子节点。
• 将 level 减去 2，设置为 6 。
• 因为 level 还是大于 0，我们继续执行 for 循环。
  • 我们再次计算 key >>> level == 636 >>> 6 。这将切掉后 6 位，剩下的是 0000 0010 01 ，也就是十进制的数字 9 。
  • 然后执行掩码运算： (key >>> level) & MASK == 9 & 3 ，换成二进制就是 1001 & 0011 ，这会消去最前头的 10 ，剩下的是 01 ，也就是十进制的数字 1。
  • 我们将当前节点 node 设置为它在位置 1 的子节点。
• 将 level 减去 2，也就是设置为 4 。
• 因为 level 还是大于 0，我们继续执行 for 循环。
  • 636 >>> 2 留给我们的是 0010 0111 00 。
  • 前面（低位）的两位是 0b00 == 0 。
  • 我们将 node 设置为它的第一个子节点，也就是索引位置为 0 的子节点。
• 将 level 减去 2，也就是设置为 0 。
• 因为 level （最终）不再大于 0，我们跳出了 for 循环。
• 我们对 key 使用 mask 做了一次掩码运算，返回二进制 10 。因此，最后我们返回 node 节点在索引位置 2 的内容。

这几乎也是你在 Clojure vector 里的执行一次查找值的操作所经历的每一步机械指令，只是深度变成了 5。这样的 vector 将包含 1 到 3300 万元素。实际上，位移和掩码运算是现代 CPU 里最高效的运算之一，所以这让整个处理过程更加有效。从性能角度来讲，查找过程剩下的唯一『痛点』是高速缓存 miss。对于 Clojure 来说，这些都交由 JVM 自身很好地被处理了。

这些就是前缀树和 Clojure Vector 实现里如何查找元素的所有内容了。我猜这里最难理解的部分是位运算，其他任何部分都非常直白。你只是需要对前缀树如何工作有一个粗略的了解，这就够了！

如果你读完这篇博客，接下来的一篇 Part 3 ，将解释 tail 引用 —— vector 的一个性能优化是如何运作的。

[1] 如果你想更学究一点，你可能想讨论这到底是不是 正式 的名称。Daniel Spiewak 在他的演讲 “Extreme Cleverness” 里将它们称为 “位映射矢量前缀树”（Bitmapped Vector Tries）。在 Clojure 社区里。他们更倾向于称之为 vector 或者 persistent vector。我们的目标并不是提供一个最广为人知的名称，而是一个名称可以在这系列博客里解释这个数据结构最重要的特性：即这是一个持久的前缀树，通过使用把元素的索引按位分区的方式来模拟一个 vector。

[2] 这里我撒了点小谎，只是为了让解释更简单一些：一些前缀树的变种可能会将它们的值实际存储在内部节点上，但是我们要讲解的这个不是这样。

[3] 尽管如此，它却可能更快！x86 上的 div 指令（除法）会把商数和余数存在两个不同的寄存器里，因此我们能承受无论如何都要执行的除法。剩下的唯一工作就是 subl 指令，它可以比取模运算更快。如果你想实现一个非常快的按数字分区的前缀树，这里需要注意下。

但是这取决于你使用的基数。在特定情况下，一个除法运算可以分解成一些位运算和乘法运算的组合，一个取模运算也可以采用类似的方式优化。

[4] 小提示：在 Java 里， >>> 是一个逻辑位移（任何移掉的多出来位都会补为 0），而 >> 是一个算术运算（移掉的位都将和最高有效位拥有同样的值）。因为我们并没有使用有符号位，所以这里其实几乎没有区别，尽管我猜测 >>> 在某些机器架构上 可能 会比 >> 更快。

对于 C/C++/GO 的朋友们来说， >>> 等同于无符号类型的 >> 。