程序性能 3-- 渐进符号

继续上一节的笔记。前2节的笔记如下：

1. 程序性能1–空间复杂性
2. 程序性能2–时间复杂性
3. 程序性能3–渐进符号

渐进符号(O,$/theta,o,/Omega$)

确定程序的操作计数和执行步数的两个重要原因如下：

1. 为了比较两个完成同一功能的程序的时间复杂性；

2. 为了预测随着实例特征的变化，程序运行时间的变化量。

   但上述两个方法都各有其缺点，使用操作计数会集中在某些”关键”的操作，而忽略了所有其他操作。使用执行步数则试图通过关注所有的操作以便克服操作技术方法的不足，但是，”执行步”的概念本身就不精确，如指令 x = y 和 x = y+z+(x/y) 都可以被称为一步。因此由于执行步数的不精确性，所以不便用来进行比较。

   因此，这里引入新的符号(或记号)，利用新符号可以写出关于程序时间和空间复杂性的具体公式(尽管不够精确)。这种符号称为 渐进符号 ，它可以描述大型实例特征下时间或空间复杂性的具体表现。

   在接下来的讨论中，$f(n)$表示一个程序的时间或空间复杂性，它是实例特征n的函数，由于一个程序的时间和空间需求是一个非负值，所以可以假定对于n的所有取值，函数$f$的值非负。由于n表示一个实例特征，所以可以进一步假定$n/ge 0$。即将讨论的渐进符号允许我们对于足够大的n值，给出$f$的上限值和/或下限值。

大写O符号

大写O符号给出了函数$f$的一个上限。

上述定义表明，函数f多是函数g的c倍，除非n小于$n_0$。因此对于足够大的n(如$n/ge n_0$)，g是f的一个上限。在为函数f提供一个上限函数g时，通常使用比较简单的函数形式，比较典型的形式是含有n的单个项(带一个常数系数)。下图列出了一些常用的g函数及其名称。下图中的对数函数$log n$，没有给出对数基，原因是对于任何大于1的常数a和b都有$log_a n = {log_b n / log_b a}$,所以$log_an$和$log_bn$都有一个相对的乘法系数$1 / log_b a$,其中a是一个常量。

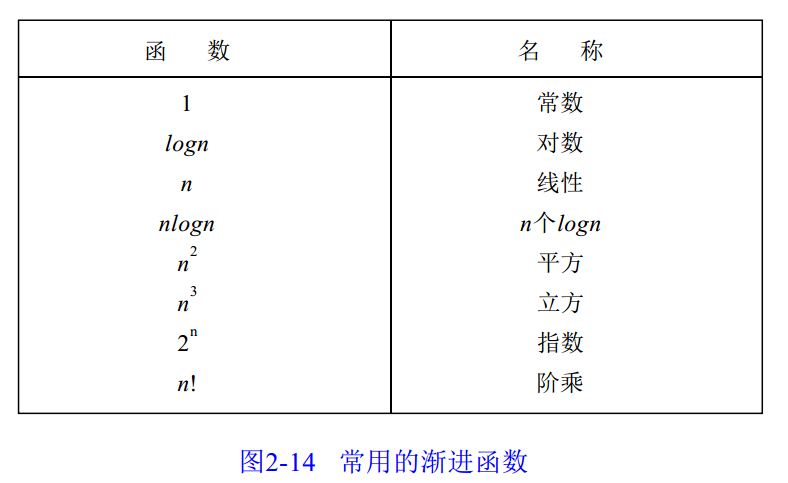
举例说明

当$n/ge 2$时，有$3n+2/ge 3n+n=4n$，所以有$f(n) = O(n)$,$f(n)$是一个线性变换的函数。当采用其他方式也可以得到同样的结论，例如,对于$n/gt 0$,有$3n+2/le 10n$,可以通过选择c=10以及$n_0/gt 0$来满足大O定义。

对于其他线性的函数，如3n+3,100n+6，都满足n的大O定义。

对于$n/ge 2$,有$f(n)/le 10n^2+5n$,而又当$n/ge 5$,有$5n/le n^2$,因此对于$n/ge n_0 = 5,f(n) /le 10n^2+n^2 = 11n^2,所以f(n) = O(n^2)$。

对于$n/ge 4,有n^2 /le 2^n，所以对于n /ge 4,有f(n) /le 6 2^n + 2^n = 7 2^n,因此6*2^n + n^2 = O(2^n)$。

松散界限

在上述例子中，如$n/ge 2,有3n+3/le 3n^2,所以3n+3=O(n^2),虽然n^2是3n+3$的一个上限，但不是最小上限，因为可以找到一个更小的函数来满足大O定义。

同样地，对于其他例子也是可以有找到其他g(n)函数来满足大O定义，但是我们需要寻找的是 最小上限 ，这也是为了让语句$f(n) = O(g(n))$有实际意义。

对于一些错误界限，如$3n+2 /neq O(1)$,可以使用反证法来证明。

下面一个定理给出了一个非常有用的结论，利用该结论可以获取f(n)的序(即$f(n) = O(g(n))$中的g(n))，这里，f(n)是一个关于n的多项式。

这里可以使用该定理来应用到前面的例子中，可以得到同样的结果。

$/Omega$符号

$/Omega$符号与大O符号类型，它用来估算函数f的下限。

上述定义表明了在$n/ge n_0$的前提下，函数f至少是函数g的c倍。与大O定义的应用一样， 通常仅使用单项形式的g函数。 同时，它也具有以下定理来求g函数。

根据这个定理可知，$3n+2 = /Omega(n)$,$10n^2+4n+2 = /Omega(n^2)$,$100n^4+3500n^2+82n+8=/Omega(n^4)$。

$/theta$ 符号

$/theta$ 符号适用于同一个函数g既可以作为f的上限也可以作为f的下限的情形。

上述定义表明了在$n/ge n_0$的情况下，函数f介于函数g的$c_1倍和c_2倍$之间。它通常仅使用单项形式的g函数。

同样地，也具有下面两个定理

根据这个定理，可知$3n+2 = /theta(n)$,$10n^2+4n+2 = /theta(n^2)$,$100n^4+3500n^2+82n+8=/theta(n^4)$。

小写o符号

例如，因为$3n+2 = O(n^2)$,且$3n+2/neq /Omega(n^2)$,所有$3n+2 = o(n^2)$,但$3n+2/neq o(n)$。

（那么其实就是可以理解为：如果$f(n) = /theta (g(n))$,则有$f(n) /neq o(g(n))$。）

特性

根据上述定理，可以有如下结论：$n^3 + n^2 logn = /theta(n^3)$(因为$n^3 /le n^3 + n^2 logn /le 2n^3$);

下面两张图，第一张图中列出了一些常用的有关$O,/Omega,/theta$的标记，在该表中除n以外所有符号均为正常数。第二张图给出了一些关于和与积的有用的引用规则，其中$/oplus 可以是O,/Omega,/theta$之一。

复杂性分析举例

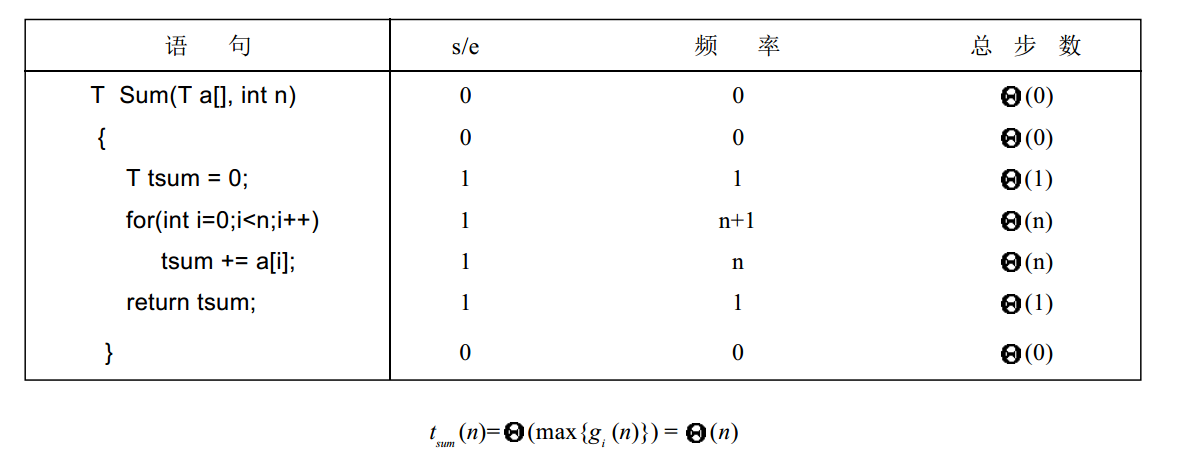
根据渐进符号，这里重新检查下上一节分析的时间复杂性，对于函数 Sum ,分析如下图所示：

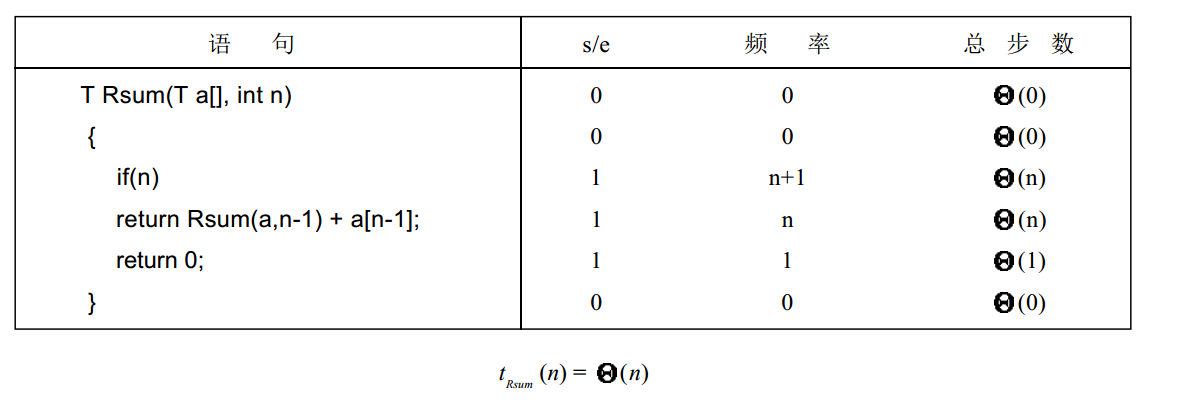
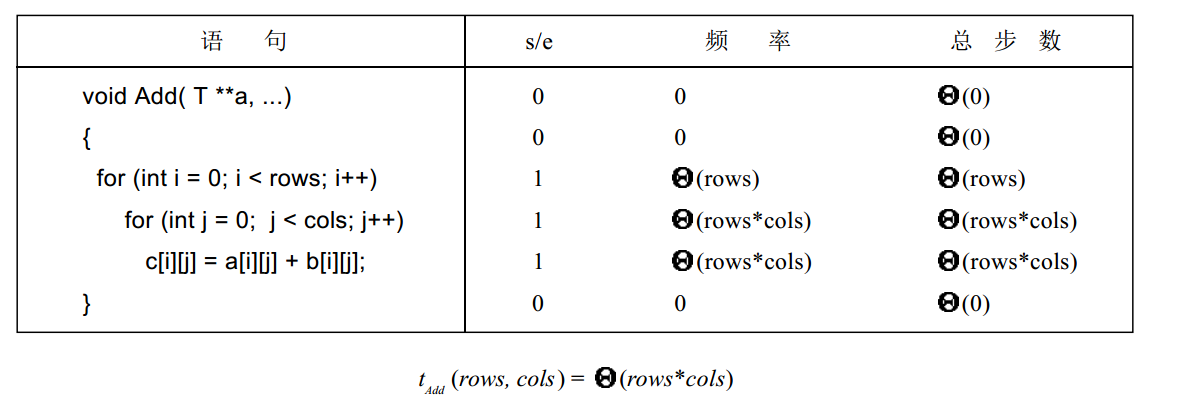
同理对于其他函数也有这样的分析，如下图所示：





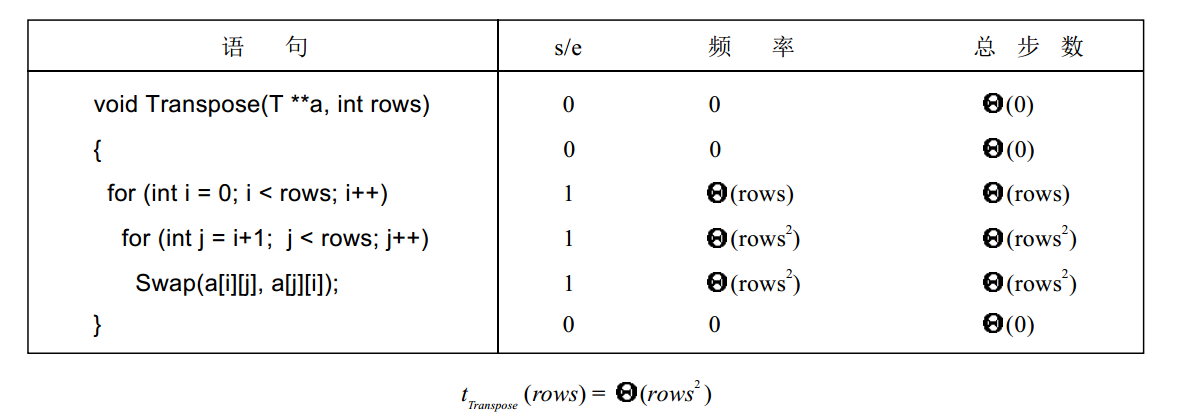
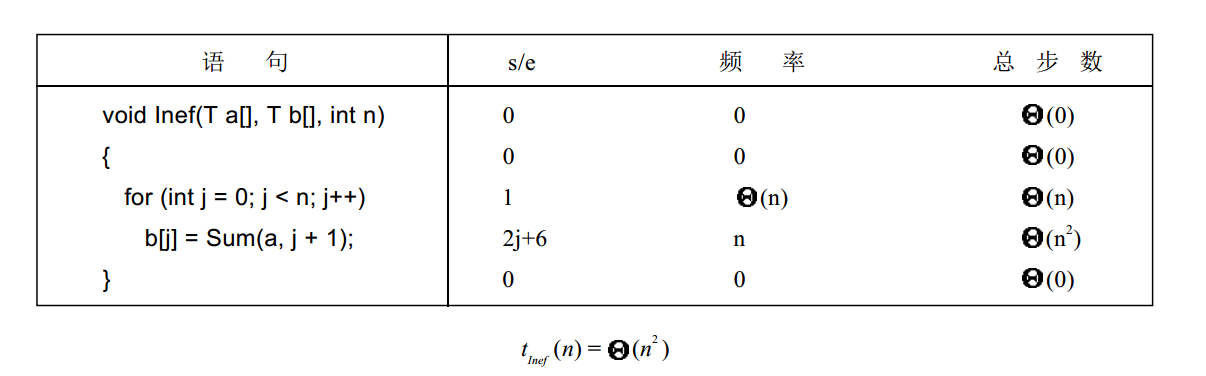
当按照执行步数来分析上述函数的时候，可以把$t_p(n) = /theta (g(n))$,$t_p(n) = O(g(n))或t_p(n) = /Omega (g(n))$看成一条程序P的语句(用于计算时间),因为每一步仅需要$/theta(1)$的执行时间。
接下来就是从全局角度来考察程序的渐进复杂性的需要，下面会举例来阐述这种方法。

/*折半搜索*/ template<class T> int BinarySearch(T a[], const T& x, int n){     int left = 0, right = n - 1;     while (left <= right){         int middle = (left + right) / 2;         if (x == a[middle])             return middle;         if (x > a[middle])             left = middle + 1;         else             right = middle - 1;     }     // 未找到x     return -1; }

在折半搜索中，While的循环(最后一次除外)都将以减半的比例缩小搜索的范围，所以该循环在最坏情况下虚执行$/theta(logn)$次，由于每次循环需要耗时$/theta(1)$，因此在最坏的情况下，总的时间复杂性是$/theta(logn)$。

第二个例子是上一节中的插入排序例子中，对于每个i值，最内部的循环在最坏情况下时间复杂性是$/theta(1)$,因此在最坏情况下，该例子的时间复杂性是$/theta(n^2)$,而最好的情况是$/theta(n)$。程序的渐进复杂性可由$/Omega(n) 和O(n^2)$给出。

小写o符号通常用于执行步数的分析。执行步数$3n+O(n)$表示3n加上上限是n的项。在进行这种分析时，可以忽略步数少于$/theta(n)$的程序部分。还可以扩充渐进符号的定义，采用具有多个变量的函数。例如，$f(n,m)=O(g(n,m))$当且仅当存在正常量$c,n_0,m_0$,使得对于所有的$n/ge n_0和所有的m/ge m_0$，有$f(n,m)/le cg(n,m)$。

实际复杂性

根据前面几节内容，我们知道一个程序的时间复杂性通常是其实例特征的函数，在确定程序的时间需求是如何随着实例特征的变化而变化时，这种函数将非常有用。
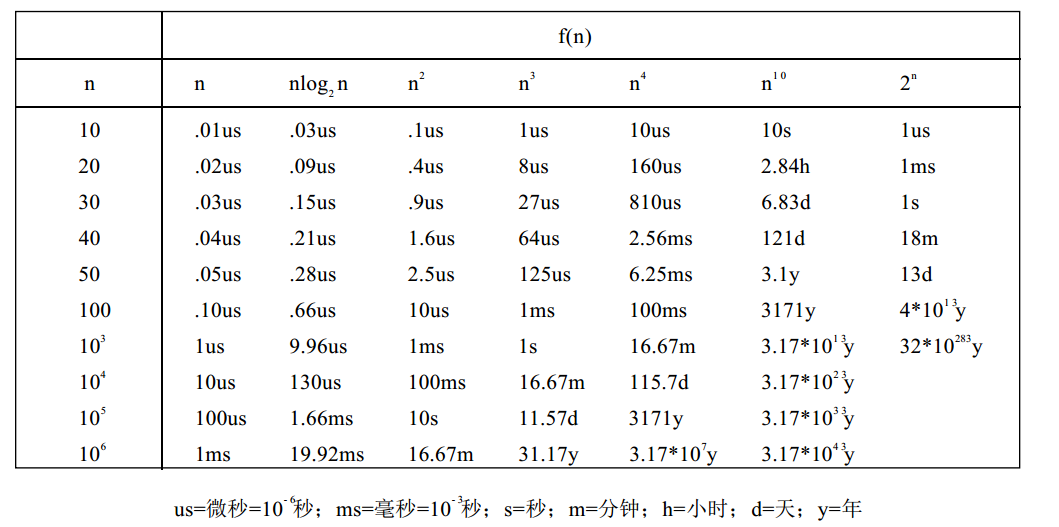
下面两张图给出各种函数是如何随着n的增长而变化的。


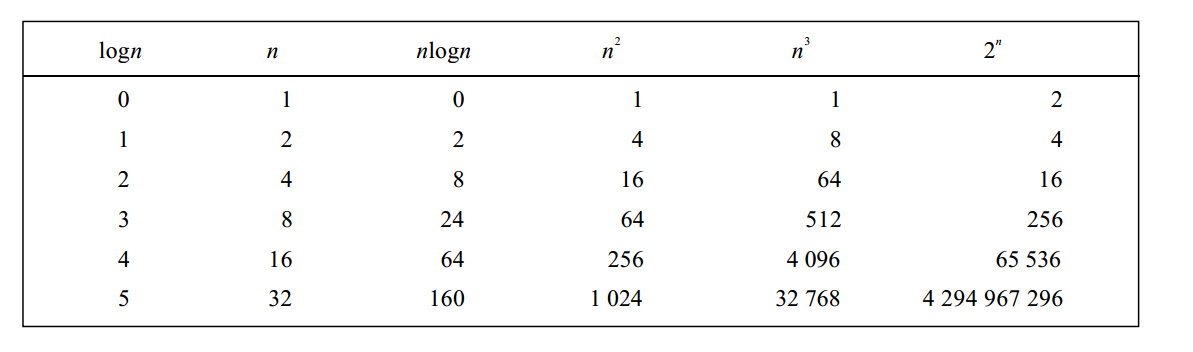
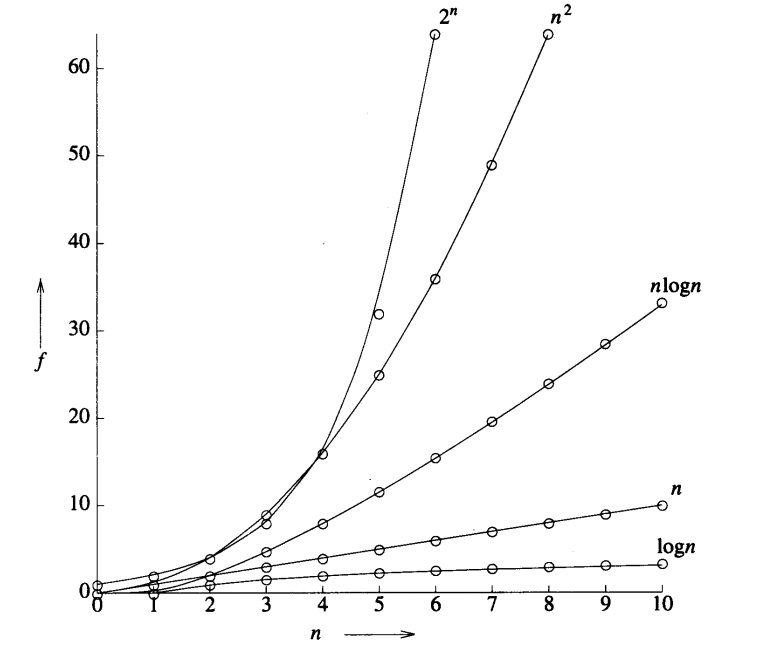
由图中可以看出随着n的增长，$2^n$的增长极快，如果需要执行$2^n$执行步，那么n=40时，执行步数将大约$1.1 10^{12}$，在一台每秒执行$10^9$步的计算机中，该程序大约需要执行18.3分钟；而如果n=50，则需要执行13天，n=60时，需要执行310.56年。因此，* 具有指数复杂性的程序仅适合于小的n(典型地取$n/le 40$)。
此外，具有高次多项式复杂性的函数也必须限制使用，比如对于需要执行$n^{10}$执行步的程序，当n=10时，同样是每秒执行$10^9$步的计算机中，需要10秒，但是n=100，这个时间就是3171年了。
下面一张图很好地给出了在每秒执行$10^9$条指令的计算机上执行复杂性是$f(n)$所需要的时间。

性能测量

我们忽略编译所需要的时间和空间是因为每个程序仅需要编译一次(当然是在调试完成之后)，而可以运行无数次。不过，如果测试的次数要比运行最终代码的次数多，则在程序测试期间，编译所需要的时间和空间也是很重要的。而基于以下原因，我们不能精确地测量一个程序运行时所需要的时间和空间:

• 指令空间和数据空间的大小是由编译器在编译时确定的，所以不必要测量这些数据。
• 根据前几节介绍的方法，可以很准确地估算递归栈空间和变量动态分配所需要的空间。

而为了得到程序的执行时间，需要一个定时机制。在C++中包含一个头文件是 time.h ，定义了一个 clock() 的函数，它可以返回自程序启动以来所流逝的“滴答”数，然后再将流逝的“滴答”数除以常量 CLK_TCK ,就可以得到流逝的秒数。

接下来，我们选择作为实验的程序是上一节中的插入排序 InsertionSort 函数。而要测量该函数在最坏情况下所需要的时间，首先需要：

1. 确定需要测定执行时间的n值；
2. 对于上面的每个n，给出能导致最坏复杂性的测试数据。

选择实例的大小

可以根据以下两个因素来确定使用哪些n值：

• 程序执行的时间
• 程序执行的次数

在之前的分析中可以知道在最坏的情况下，插入排序的复杂性是$/theta(n^2)$。实践过程中，通常需要3个以上的n值，其原因如下：

1. 渐进分析仅给出了对于足够大的n值时程序的复杂性。对于小的n值，程序的运行时间可能并满足渐近曲线。为了确定渐近曲线以外的点，需要使用多个n值。
2. 即使在满足渐近曲线的区间内，程序实际运行时间也可能不满足预定的渐近曲线，原因是在进行渐进分析时，忽略了许多低层次的时间需求。例如，一个程序的渐进复杂性是$/theta(n^2)$，而它的实际复杂性可以是$c_1n^2+c_2nlogn+c_3n+c_4$,或其他任何最高项是$c_1n^2$的函数，其中$c_1$是常数且大于0。

而在我们用来实验的插入排序程序，我们期望获得$n/lt 100$的渐进复杂性，所以对于$n/gt 100$的情况，可能只需奥很少量的估算值，一个合理的选择是$n=200,300,400,/ldots,1000$。

设计测量数据

对于许多程序，可以手工或者用计算机来产生能导致最好和最后复杂性的测试数据。然而，对于平均的复杂性，通常很难设计相应的数据。如对于我们要用来实验的 InsertionSort 函数来说，对任何n来说，能导致最坏复杂性的测试数据应是一个递减的序列，如$n,n-1,n-2,/ldots,1$;导致最好复杂性的测试数据应是一个递增的序列，如$0,1,2,/ldots,n-1$。我们很难提供一组测试数据使得 InsertionSort 函数表现出平均的复杂性。

进行实验

当确定了实例大小，并给出了测试数据，就可以开始进行实验了。实验运行的代码如下所示:

#include<iostream> #include<string> #include<time.h>  /*向一个有序数组中插入元素,假定a的大小超过n*/ template<class T> void Insert(T a[], int& n, const T& x){     int i;     for (i = n - 1; i >= 0 && x < a[i]; i--)         a[i + 1] = a[i];     a[i + 1] = x; }  template<class T> void InsertionSort(T a[], int n){     for (int i = 1; i < n; i++){         T t = a[i];         Insert(a, i, t);     } }  int main(){     using std::cout;     using std::endl;     using std::cin;      int a[1000], step = 10;     clock_t start, finish;     for (int n = 0; n <= 1000; n += step) {         for (int i = 0; i < n; i++)             a[i] = n - i; // 初始化         start = clock();         InsertionSort(a, n);         finish = clock();         cout << n << ' ' <<(float)(finish - start) / CLK_TCK << endl;         if (n == 100)              step = 100;     }     system("pause");     return 0; }

实验结果如下图所示

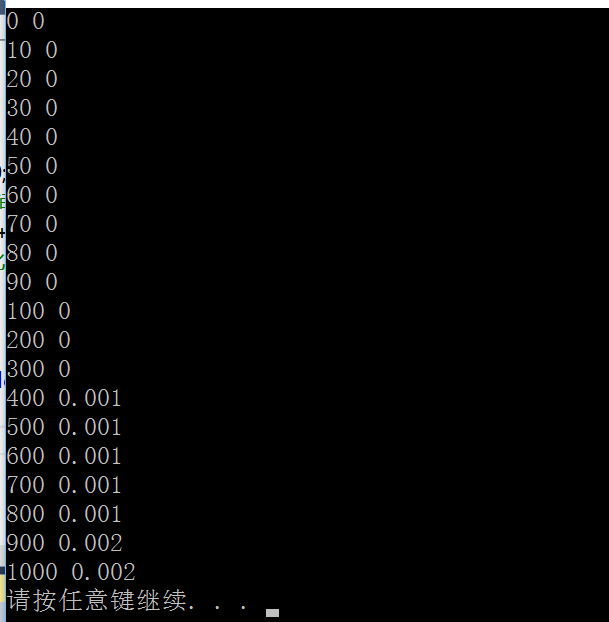
由上图可以得出这样的结论，排序300个元素以内的数组不需要时间，而排序400-800个元素的数组所花费的时间是一样的。但这个结论并不正确，主要是因为对于计时函数 clock() 来说，所需要的运行时间太小了。而且，所有测量的精确度均为一个时钟“滴答”。书本中使用的计算机的 CLK_TCK=18.2 ,不过我使用的是 Visual Studio 中 CLK_TCK=1000 ,即这里测量的误差范围是一个“滴答”时间 1/1000 = 0.001 秒。
而为了提高测量的精确度，对于每个n值，可以重复排序若干次。这里限定的条件是10个时钟“滴答”时间。代码及实验结果如下所示：

#include<iostream> #include<string> #include<time.h>  /*向一个有序数组中插入元素,假定a的大小超过n*/ template<class T> void Insert(T a[], int& n, const T& x){     int i;     for (i = n - 1; i >= 0 && x < a[i]; i--)         a[i + 1] = a[i];     a[i + 1] = x; }  template<class T> void InsertionSort(T a[], int n){     for (int i = 1; i < n; i++){         T t = a[i];         Insert(a, i, t);     } }  int main(){     using std::cout;     using std::endl;     using std::cin;      int a[1000],n,i, step = 10;     long counter;     float seconds;     clock_t start, finish;     for (int n = 0; n <= 1000; n += step){         // 获得对应于n值的时间         start = clock();         counter = 0;         while (clock() - start < 10){             counter++;             for (i = 0; i < n; i++)                 a[i] = n - i;             InsertionSort(a, n);         }         finish = clock();         seconds = (float)(finish - start) / CLK_TCK;         cout << n << ' ' << counter<<' ' << seconds<<' '<< seconds/counter<< endl;         if (n == 100)             step = 100;     }     system("pause");     return 0; }

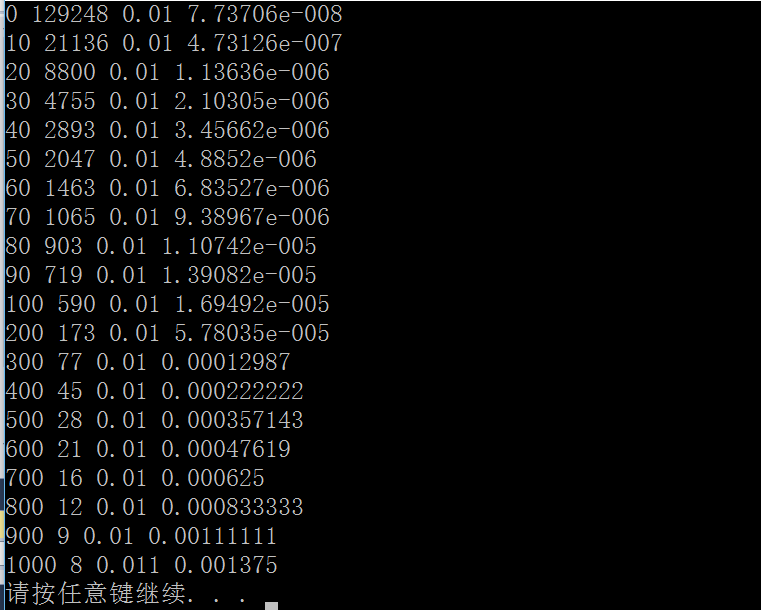
上图中每行数据分别是n值，重复次数，总时间以及每次排序时间。

小结

第二章有关程序性能的笔记就记录到这里了。本章主要是介绍了算法的基础，对于程序的空间和时间复杂性的介绍，还介绍了4种渐进符号，然后就是给出了一个例子来测量运行时间。本章是一个学习数据结构和算法的基础，因为我还是初学者，所以笔记主要是记录书中的要点，比较少有写上自己的理解，不过，相信随着练习，会慢慢掌握数据结构和算法的知识点的。