机器学习笔记1--机器学习简介
对于机器学习，并没有一个一致认同的定义，一个比较古老的定义是由 Arthur Samuel 在1959年给出的：
机器学习研究的是如何赋予计算机在没有被明确编程的情况下仍能够学习的能力。(Field of study that fives computers the ability to learn without being explicily programmed.)
随后他编写了一个跳棋游戏的程序，并且让这个程序和其自身玩了几万局跳棋游戏，并且记录下来棋盘上的什么位置可能会导致怎样的结果，随着时间的推移，计算机学会了棋盘上的哪些位置可能会导致胜利，并且最终战胜了设计程序的Samuel。
另一个比较现代且形式化的定义是由 Tom Mitchell 在1998年给出的：
对于某个任务T和表现的衡量P，当计算机程序在任务T的表现上，经过P的衡量，随着经验E而增长，我们便称计算机程序能够通过经验E来学习该任务。
在上述的跳棋游戏的例子中，任务T是玩跳棋游戏，P是游戏的输赢，而经验E则是一局局的游戏。
一些机器学习的应用例子：
- 数据挖掘
- 一些无法通过手动编程来编写的应用：如自然语言处理，计算机视觉
- 一些自助式的程序：如推荐系统
- 理解人类是如何学习的
监督学习(Supervised Learning)
首先是举出一个房价的例子，如下所示:
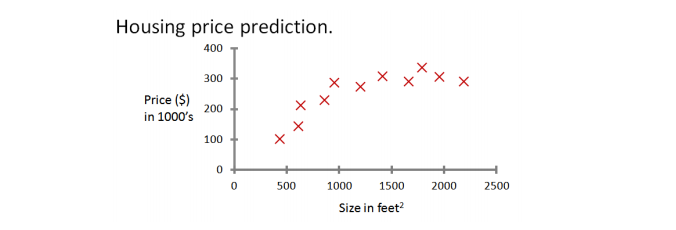
即通过给出房子面积和房价的一些数据，来预测一个新的房子面积所能卖出的房价。
所以，监督学习是指给出标记的数据集，并且已知输入和输出的关系。
监督学习分为两类问题，分别是回归问题和分类问题。回归问题的输出是一个连续值，比如在预测房价这个例子中，预测房价是一个回归问题，其结果是连续值。而分类问题是得到一个离散值的输出，比如同样是预测房价的例子，如果问题从预测卖出的房价变成卖出的房价是偏高还是偏低，就是属于分类问题，因为其答案可以用0或1表示高了或者低了。
课程中给出另一个例子说明分类问题，如下图所示：
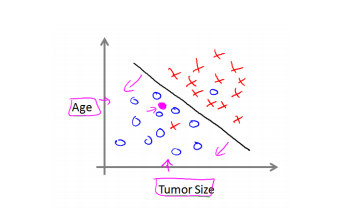
问题是假设预测一个乳腺癌是否是恶性的，图中坐标轴横轴表示肿瘤的大小，纵轴表示病人的年龄，以O表示良性肿瘤，以X表示恶性肿瘤。所以问题就是判断是良性还是恶性肿瘤，这就是一个分类问题。
非监督学习(Unsupervised Learning)
在监督学习中，无论是回归问题还是分类问题，数据集都有一个明确的结果。
而在非监督学习中，数据并没有一个结果，有的只是特征，即非监督学习要解决的问题是这些数据是否可以分成不同的组。
而非监督学习中典型的例子就是聚类问题。例如对一个大型的数据中心的网络传输数据情况进行分析，发现那些多数时候是在协作的计算机。
课程小结
这是3个小节课程的笔记，主要是对机器学习的介绍，然后介绍了机器学习中的两大学习问题，监督学习和非监督学习。
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
