转载

数据描述2--单向链表

继续是《数据结构算法与应用：C++语言描述》第3章数据描述的笔记。本小节主要介绍链表，以及单向链表的代码实现。

链表描述

类ChainNode和Node

链表描述中，数据对象实例的每个元素都放在单元或节点中进行描述，不过每个节点不必是一个数组元素，但都包含了与该节点相关的其他节点的位置信息，这种关于其他节点的位置信息被称为链(link)或指针(pointer)。

令$L=(e_1,e_2,/ldots,e_n)$是一个线性表，其链表描述如下图所示，每个节点都包含一个链接域，用以指向表中的下一个元素。所以节点$e i$的指针将指向$e {i+1}$，其中$1/le i /lt n$。节点$e_n$没有下一个节点，所以它的链接域是NULL(或0)。指针变量 first 指向描述中的第一个节点。
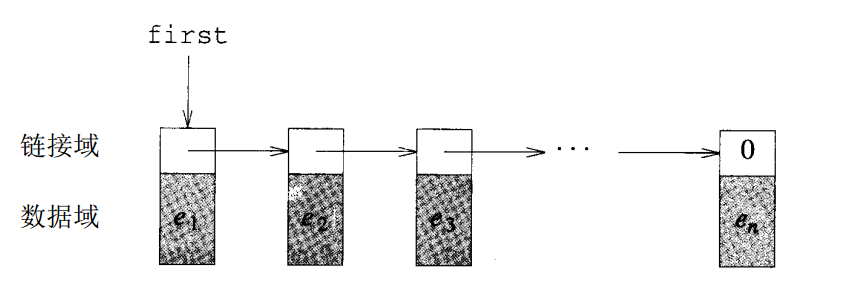
数据描述2--单向链表

上图中每个节点都正好有一个链接域，所以该图的链表结构被称之为 单向链表 ，此外，这种结构由于是每个节点的指针都指向下一个节点，然后最后一个节点的链接域是NULL，故也称为 链(chain) 。这里定义的 Chain<T> 是 ChainNode<T> 的一个友类，即 Chain<T> 可以访问 ChainNode<T> 的所有成员(尤其是私有成员)。其类定义如下：

#include<iostream>  // 必须先声明，否则友元模板类之间无法直接访问，会出现未定义的错误。 template<class T> class Chain;   template<class T> class ChainNode{     friend Chain<T>; private:     T data;     ChainNode<T> * link; };  template<class T> class Chain{ private:     // 指向第一个节点的指针     ChainNode<T> *first; public:     Chain(){ first = 0; }     ~Chain();     bool isEmpty() const{ return first == 0; }     int Length() const;     bool Find(int k, T& x)const;     int Search(const T& x)const;     Chain<T>& Delete(int k, T& x);     Chain<T>& Insert(int k, const T&x);     void Output(std::ostream& out)const; };

操作

下面给出析构函数， Length,Find,Search,Output 函数的代码实现，其中析构函数的复杂性是$/theta(n)$,n是链表的长度，而 Length 的复杂性是$/theta(n)$, Find 的复杂性$O(k)$,函数 Search 的复杂性是$O(n)$, Output 的复杂性是$/theta(n)$。

template<class T> Chain<T>::~Chain(){     // 删除链表中的所有节点     ChainNode<T> *next;     while (first){         next = first->link;         delete first;         first = next;     } }  template<class T> int Chain<T>::Length() const{     // 返回链表中的元素总数     ChainNode<T> *current = first;     int len = 0;     while (current){         len++;         current = current->link;     }     return len; }  template<class T> bool Chain<T>::Find(int k, T&x)const{     // 寻找链表中的第k个元素，并将其传送者x     if (k < 1)         return false;     ChainNode<T> *current = first;     // current的索引     int index = 1;       while (index < k && current){         current = current->link;         index++;     }     if (current){         x = current->data;         return true;     }     // 不存在第k个元素     return false; }  template<class T> int Chain<T>::Search(const T& x)const{     // 寻找x，如果发现x，则返回x的位置     ChainNode<T> *current = first;     // current的索引     int index = 1;     while (current && current->data != x){         index++;         current = current->link;     }     if (current)         return index;     return 0; }  template<class T> void Chain<T>::Output(std::ostream& out)const{     //  将链表元素送至输出流     ChainNode<T> *current;     for (current = first; current; current = current->link){         out << current->data << " ";     } } // 重载 << template<class T> std::ostream& operator<<(std::ostream& out, const Chain<T>& x){     x.Output(out);     return out; }

删除操作

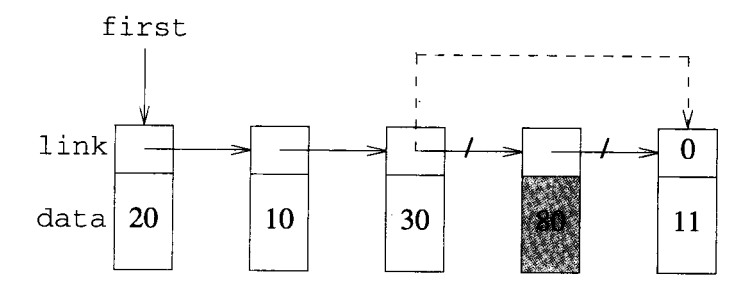
假如要从下图中删除第四个元素，需要进行如下操作：

找到第三和第四个节点；
使第三个节点指向第五个节点；

释放第四个节点所占空间，以便于重用。
数据描述2--单向链表

代码实现如下：

template<class T> Chain<T>& Chain<T>::Delete(int k, T&x){     // 把第k个元素取至x，然后删除第k个元素     if (k < 1 || !first)         // 不存在第k个元素         throw OutOfBounds();     // p最终指向第k个节点     ChainNode<T> *p = first;     if (k == 1)         // p已经指向第k个元素         first = first->link;     else{         // q用于移动到第k-1个节点         ChainNode<T>*q = first;         for (int index = 1; index < k - 1 && q; index++)             q = q->link;         if (!q || !q->link)             // 不存在第k个元素             throw OutOfBounds();         // 存在第k个元素         p = q->link;         // 让上一个节点指向待删除节点后面的节点         q->link = p->link;     }     // 保存第k个元素的值，然后释放节点     x = p->data;     delete p;     return *this; }

这里有三种情形要考虑，分别如下：

k小于1或链表为空；
第一个元素将被删除且链表不为空；
从一个非空的链表中删除非首元素的元素。
程序中首先就处理第一种情形，即引发 OutOfBounds 异常。然后声明一个指针变量 p 用于最终指向第k个元素，对于第二种情形，语句 first = first->link; 就可以用来删除第一个元素；对于第三种情形，首先是定义了新的指针变量 q ，然后通过一个for循环让q定位到第k-1个元素，此时如果链表的节点数少于k-1，则q为0，也是引发 OutOfBounds 异常，否则就让p指向第k个元素，并保存其值，然后释放该节点。

插入操作

插入操作和删除操作很相似，要在链表第k个元素之后插入一个新的元素，需要首先找到第k个元素，然后在该节点后面插入新的节点。程序实现如下所示，其时间复杂性是$O(k)$。

template<class T> Chain<T>& Chain<T>::Insert(int k, const T& x){     // 在第k个元素后面插入x     if (k < 0)         throw OutOfBounds();     ChainNode<T> *p = first;     for (int index = 1; index < k && p; index++)         p = p->link;     if (k>0 && !p)         // 不存在第k个元素         throw OutOfBounds();     ChainNode<T> *newNode = new ChainNode<T>;     newNode->data = x;     if (k){         newNode->link = p->link;         p->link = newNode;     }     else{         // k=0,即作为第一个元素插入         newNode->link = first;         first = newNode;     }     return *this; }

同样在插入操作中需要注意的是$k=0$和$k /neq 0$两种情形下的插入操作，前者是作为第一个元素插入，需要使用到指向第一个节点的指针 first 。

扩充类Chain

这里会在之前的抽象数据类型 LinearList 中的操作上增加一些新的方法，比如 Erase （删除链表中的所有节点)、 Zero (将first指针置为0，但并不删除任何节点)、 Append (在链表的尾部添加一个元素)。
对于函数 Erase ，其等价于类的析构函数，实现如下所示：

// 删除链表中的所有节点 template<class T> void Chain<T>::Erase(){     ChainNode<T> *next;     while (first){         next = first->link;         delete first;         first = next;     } }

而函数 Zero 则可以定义为如下的内联函数：

void Zero() { first = 0; }

对于函数 Append ，为了在$/theta(1)$的时间内添加一个元素，需要在类中添加一个新的类型是 ChainNode<T> * 的私有成员 last 来跟踪链表的最后一个元素。同时需要在插入和删除操作中各自添加一条语句，即在 Delete 函数中的语句

// 存在第k个元素 p = q->link;

后面增加下列语句

// 如果刚好是第k个节点是最后一个节点 if (p == last)     last = q;

在 Insert 操作中的语句

return *this;

前面添加下面的语句

// 如果新插入的节点是最后一个节点 if (!newNode->link)     last = y;

最后， Append 函数的代码实现如下：

// 在链表末尾右端添加一个元素 template<class T> Chain<T>& Chain<T>::Append(const T&x){     ChainNode<T> *newNode;     newNode = new ChainNode<T>;     newNode->data = x;     newNode->link = 0;     if (first){         // 链表非空         last->link = newNode;         last = newNode;     }     else{         first = last = newNode;     }     return *this; }

这里需要判断链表是否为空的问题，如果是空，则令 first = last = newNode ;

链表遍历器类

这里使用一个链表遍历器，遍历器的功能是记录当前位置并每次向前移动一个位置。在如下实现的遍历器程序中，有两个共享成员 Initialize 和 Next 。
Initialize 返回一个指针，其指向第一个链表节点中包含的数据，同时把私有变量 location 设置为指向链表的第一个节点，该变量用来跟踪我们在链表中所处的位置。而成员 Next 用来调整 location ，使其指向链表中的下一个节点，并返回指向该节点数据域的指针。由于遍历器类访问了 Chain 类的私有成员，所以应把它定义为 Chain 的友类(实际上应该还需要定义为 ChainNode 的友类，因为也是访问了其私有成员 data )。

// 链表遍历器类 template<class T> class ChainIterator{ private:     ChainNode<T> *location; public:     T* Initialize(const Chain<T>& c){         location = c.first;         if (location)             return &location->data;         return 0;     }     T* Next(){         if (!location)             // 链表为空             return 0;         location = location->link;         if (location)             return &location->data;         return 0;      } };

其使用例子如下,此时 Output 函数不是 Chain 类的成员函数。

template<class T> void Output(const Chain<T>& X){     int *x;     ChainIterator<T> c;     x = c.Initialize(X);     while (x){         cout << *x << ' ';         x = c.Next();     }     cout << endl; }

使用遍历器可以实现在线性时间内输出链表，如上述程序所示。

更完整的例子可以查看 ChainList 。

原文 http://ccc013.github.io/2016/06/09/数据描述2-单向链表/

正文到此结束