转载

机器学习之逻辑回归

在上一篇机器学习之感知机中，我们实现了一种简单的线性分类模型感知机模型，它有很大的局限性。
感知机的目标仅仅是正确的将线性可分的数据集分开，在实验结果中也可以看到得到的分离超平面与其中一类较近，与另一类较远，这是因为一旦对所有样本都正确的分类，算法就停止了迭代。
感知机的另一个问题是如果数据集线性不可分，将永远不会收敛，虽然我们可以人为的在迭代了若干轮之后停止迭代，但何时停止结果最好并未可知。
这些问题的根源在于感知机的目标函数是基于误分类点的，对于正确分类的样本其实是没有再使用到的，这就导致学习到的参数不够好。
逻辑回归模型将定义一个更为合理的目标函数。

什么是逻辑回归（logistic regression）

逻辑回归(逻辑斯蒂回归,logistic regression)，是一种经典的二类分类模型，虽有回归二字，却不是回归模型，名字中带有回归两个字是因为其与线性回归中的 $/theta$ 参数形式类似。
逻辑回归与逻辑二字完全无关，属于logistic的音译，之所以有logistic这个词，是因为模型中使用到了logistic函数，又称为sigmoid函数，是一种取值在0到1的S形函数。
逻辑回归是一种判别模型（discriminant model），学习的是给定特征条件下属于每种类别的概率，即 $p(y/mid{x})$, 与之相反的叫做生成模型（generative model），学习的是特征与类别的联合概率，即 $p(x,y)$。
逻辑回归可以泛化成一种多类分类模型，叫做 softmax regression，本文先讨论用逻辑回归解决二类分类问题。

逻辑回归模型

logistic函数

我们定义 $y$ 是一个样本对应的类别，在感知机中取值是-1和+1，在这里取值是0和1，即 $y/in/lbrace0,1/rbrace$ ，这仅是为了计算方便。
逻辑回归与线性回归的相似之处在于，要学习的也是一组 $/theta$ 参数，是一个 $n+1$ 维的向量，n是特征维度，加一是进行了增广，有下式成立，其中 $x_0=1$：
$$
{/theta}^{T}x=/theta_0x_0+/theta_1x_1+/theta_2x_2+…+/theta_nx_n
$$
逻辑回归的最终输出是0或1，因此不能像线性回归一样直接将上式作为输出，因为那并不能得到一个好的结果，我们使用一个logistic函数将上式映射到0与1之间，或称为logit函数或者sigmoid函数。logistic函数定义如下：
$$
g(z)=/frac{1}{1+e^{-z}}
$$
logistic函数的图形如下：

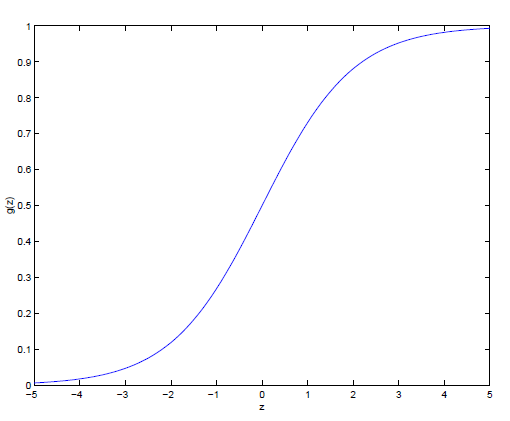
机器学习之逻辑回归

可以看到，当自变量取值0时，函数值为0.5，自变量趋向于正无穷和负无穷时函数值趋近于1和0。因此我们用下式表示对一个样本 $x$ 的预测：
$$
h_/theta(x)=g({/theta^T}{x})=/frac{1}{1+e^{-{/theta^T}{x}}}
$$
这个结果将位于0和1之间，在学习好参数之后，我们可以认为这个结果与0和1哪个更近，就将哪个类别作为这个测试样本的预测类别。

目标函数

事实上，逻辑回归做出了如下假设：
$$
P(y=1{/mid}{x};{/theta})=h_/theta(x)
$$
$$
P(y=0{/mid}{x};{/theta})=1-h_/theta(x)
$$
将logistic函数得到的函数值认为是类别为1的概率，1减去这个值就是类别为0的概率。这两个概率可以写成一个式子来表示：
$$
P(y{/mid}{x};{/theta})={(h_/theta(x))}^{y}{(1-h_/theta(x))}^{1-y}
$$
那么我们要定义参数的似然性来作为目标函数，然后学习得到使得这个似然性不断增大最终收敛时的参数 $/theta$。参数似然性表示如下：
$$
L(/theta)=p(Y/mid{X};/theta)=/prod_{i=1}^{m}p(y^{(i)}{/mid}x^{(i)};/theta)=/prod_{i=1}^{m}{(h_/theta(x^{(i)}))^{y(i)}}{(1-h_/theta(x^{(i)}))^{1-y^{(i)}}}
$$
可以看到这个似然性是使得这整个数据集的条件概率。为了计算方便，定义对数似然如下：
$$
l(/theta)=log(L(/theta))=/sum_{i=1}^{m}y^{(i)}logh_/theta(x^{(i)})+(1-y^{(i)})log(1-h_/theta(x^{(i)}))
$$

最大化参数似然性

那么如何来最大化这个对数似然函数呢？显然可以使用梯度下降法，只不过这一次是梯度上升。
对对数似然求参数导数，得到:
$$
/frac{/partial}{/partial{/theta_j}}l(/theta)=/sum_{i=1}^{m}(y^{(i)}-h_/theta(x^{(i)}))x^{(i)}_j
$$
从而可以得到批梯度下降的参数更新公式：
$$
/theta_j=/theta_j+/alpha/sum_{i=1}^{m}(y^{(i)}-h_/theta(x^{(i)}))x^{(i)}_j=/theta_j+/alpha/sum_{i=1}^{m}(y^{(i)}-/frac{1}{1+e^{-{/theta^T}{x^{(i)}}}})x^{(i)}_j
$$
去掉其中的 $/sum_{i=1}^{m}$ 就可以得到随机梯度下降的参数更新公式。

逻辑回归模型的实现

以一个简单的例子来实现一个逻辑回归模型。
6个训练样本的特征分别为(3,3), (3,4), (2,4), (-1,1), (-1,2), (1,1)对应的类别分别是1,1,1,0,0,0。现在要学习一个逻辑回归模型,并预测3个测试样本(2,1),(2,2),(2,3)的类别。
给出matlab实现代码。

load data;
X = [ones(size(train_feature,1),1) train_feature];
n = size(X,2); %特征数+1
m = size(X,1); %样本数
Y = train_label; %真实类别
theta = zeros(n,1); %参数
theta_new = zeros(n,1);
epsilon = 0.0001; %收敛阈值
alpha = 0.01; %学习率
% 训练
while 1
    for(j = 1:n)
        theta_new(j) = theta(j);
        for(i = 1:m)
            h = 1/(1+exp(-theta'*X(i, :)'));
            theta_new(j) = theta_new(j) + alpha * (Y(i)-h) * X(i, j); 
        end;
    end;
    if norm(theta_new-theta) < epsilon
        theta = theta_new;
        break;
    else
        theta = theta_new;
    end;
end;
% 测试
test_feature = [ones(size(test_feature,1),1) test_feature];
predict=[];
predictLabel=[];
for i=1:size(test_feature,1)
    predict=[predict;1/(1+exp(-theta'*test_feature(i,:)'))];
    if 1/(1+exp(-theta'*test_feature(i,:)'))>=0.5
        predictLabel=[predictLabel;1];
    else
        predictLabel=[predictLabel;0];
    end;
end;

这里使用了批梯度下降法来更新参数，测试时predict是预测该样本处于类别1的概率，predictLabel是预测的类别，只要和0.5比较即可。
下面这段代码用于计算参数的似然性，这里只是用来分析似然性的变化情况，使用逻辑回归时无需计算。
一般情况下，参数的似然性 $L(/theta)$ 会随着迭代不断递增的，当学习率特别大的情况下，可能会出现不增反降的情形。

% 计算参数的似然性(仅用作分析)
L(k) = 0;
for(i = 1:m)
    h = 1/(1+exp(-theta'*X(i, :)'));
    L(k) = L(k) + (Y(i)*log(h) + (1-Y(i))*log(1-h));
end;
L(k) = exp(L(k));
fprintf('The %dth iteration, L = %f /n', k, exp(L(k)));

据此画出了参数似然性随着迭代次数的变化图，可以看到似然性不断逼近1。

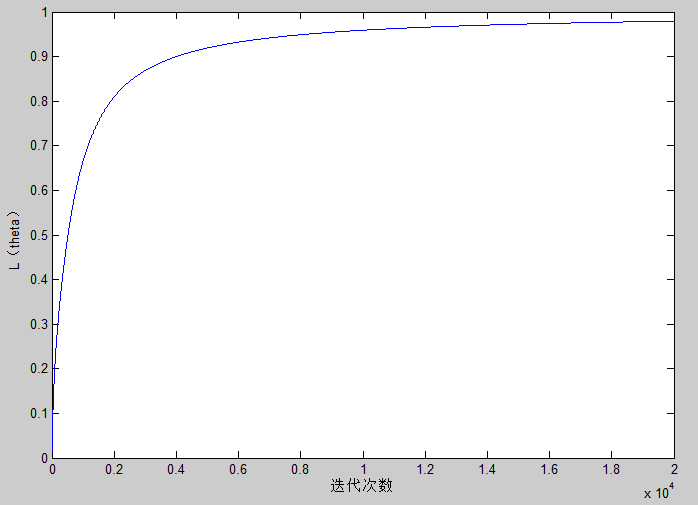
机器学习之逻辑回归

逻辑回归得到的参数以及预测的结果见下图。

机器学习之逻辑回归

参数 $/theta=[-9.3813;2.4955;2.5963]$, 这就表示决策线的直线方程为 $2.4955x+2.5963y-9.3813=0$, 在这条直线上方的就是正类，下方则是负类。
可以看到(2,1)预测为负类，(2,2)和(2,3)预测为正类，同时可以看到这三个点预测为正类的概率，点(2,2)距离决策线很近，因此该点预测为正类的概率比较接近于0.5。
最后用图形直观的对比一下逻辑回归模型与感知机模型的实验结果。

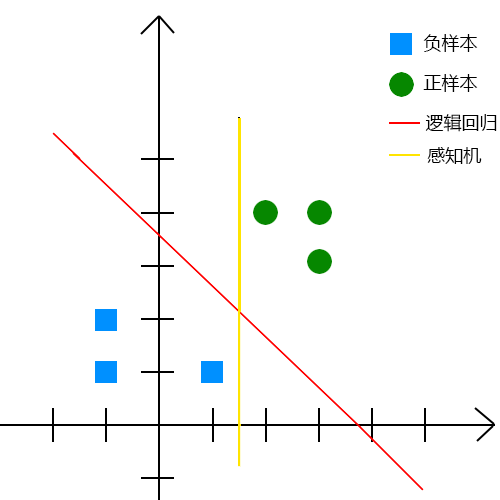
机器学习之逻辑回归