翻译:深入理解 Clojure Persistent Vectors 实现 Part 3
前言
原文地址: http://hypirion.com/musings/understanding-persistent-vector-pt-3
为什么翻译这系列博客?一直觉着翻译是学习的笨功夫,阅读一遍可能理解了概要,但是其实还是有很多细节遗漏了,翻译这个过程可以查缺补漏,更重要的是,我想重新写博客了 :D。
正文
关于 Clojure Persistent vectors 这个系列博客的Part 1和Part 2 应该可以让你对 persistent vector 的工作原理的有个大概的了解,但是,其实这里仍然有许多不同的方法可以消减(算法)的常数因子(的影响)。可能最容易理解的部分是 尾部 (tail),我们将在这篇博客里介绍。
尾部的基本原理
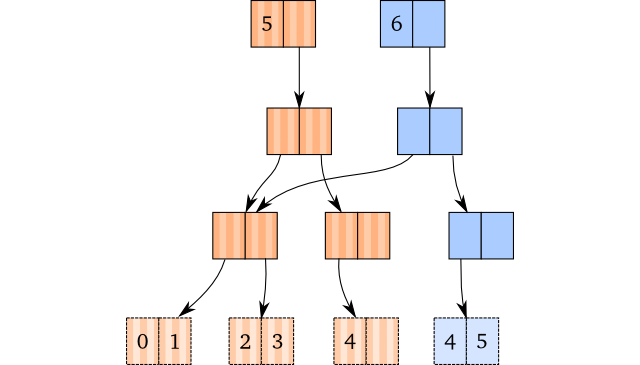
回想下 (conj [1 2 3 4] 5) 这个操作的可视化展示,没有任何尾部实现时:如果在最右叶子节点有空间,我们仅需要拷贝向下到达该叶子节点的路径,并将最后这个新元素插入到拷贝中。
有尾部的时候会有什么不同呢?让我们瞧下:
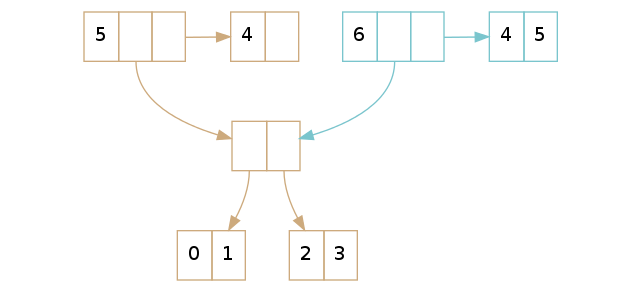
不再是在树里面保存最右叶子节点,取而代之,我们在 vector 的头部(header)就持有一个它的直接引用:这是上篇博客后加入 vector 头部的最后部分。 指向最右叶子节点的引用称为尾部 。
对于 conj 操作,我们以检测尾部有没有足够空间而告终。因为这里刚好是这种情况 —— 我们拷贝了尾部,并将新元素插入其中。请注意 这是常量时间 ,不是 近乎 常量时间。所以,每次在尾部有空余空间的时候,我们 conj 新元素到 vector 的时候,我们都是在做常量时间的操作。
这使得批量操作变得特别快。如果你接连做大量的 conj 操作,结果是每个操作的耗时平均起来更少。对于一个分支因子是 2 的 vector, 1/2(50%) 的 conj 操作(平均起来)是常量时间。如果将分支因子替换成 32, 31/32 的所有 conj 操作都将实际上是常量时间。只有 3.1% 的操作是 近乎 常量时间,意味着我们得到一个相当显著的常数削减。对于连续的 disj 操作我们也得到同样的性能好处。
所以这看起来是非常吸引人的改进。但是我们如何实现它呢?
尾部偏移量(tail offset)
在我们了解如何实现实际操作之前,我们需要学习一个很容易理解的概念:一个 vector 的 尾部偏移量 。为了理解 vector 一些操作需要做的修改,我们需要了解这个概念。
尾部偏移量其实就是元素在一棵树里的总量(译者注:请注意,现在最右叶子节点不在树里了,而是在 vector 头部作为尾部存在,因此树里的元素是减少了)。在实践中,就是 tail_offset = vector.length - tail.length 。就是这么一个公式,没有比这个公式更多的解释了。我们需要尾部偏移量的理由是,有的时候我们需要回去执行『老的』操作:查找或者修改元素要求我们知道它们是不是在树里,或者是否在尾部里。
举一个尾部偏移量的例子,回想下前文提到的 5 个和 6 个元素的 vector。5 个元素的 vector 在它的尾部里只有一个元素,所以他的尾部偏移量是 4(译者注:vector 长度 5 减去尾部长度 1,结果为 4,后文类似)。拥有 6 个元素的 vector 的尾部偏移量也是 4, 因为它的 尾部引用有 2 个元素。
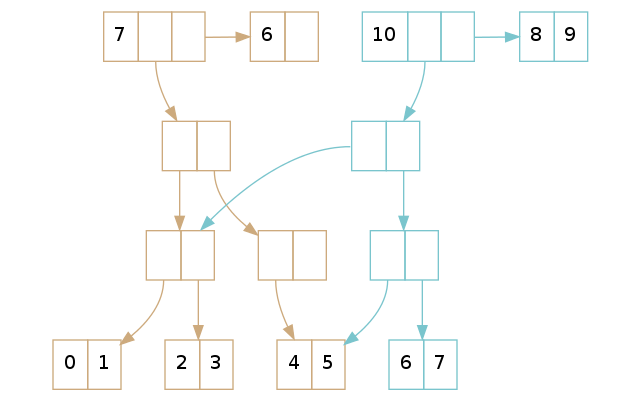
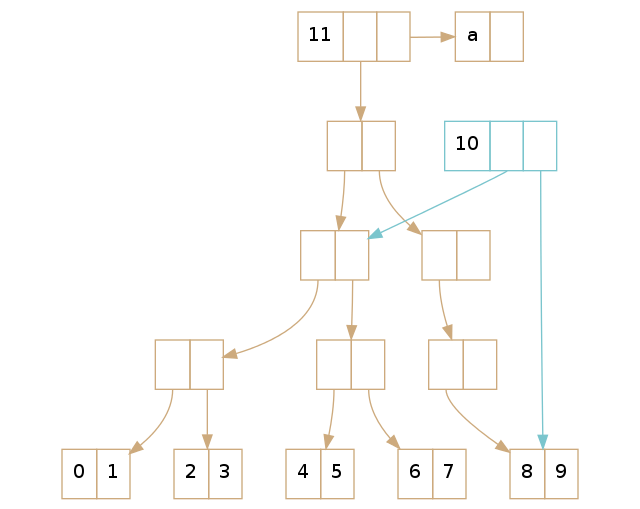
更多尾部偏移量的例子请参考上图中的两个 vector。拥有 7 个元素的 vector 的尾部偏移量是 6,而有 10 个元素的 vector 的尾部偏移量是 8。
查找
有没有尾部引用,对于在 vector 中查找一个值的过程来说并没有太大的不同。从根本上有两种情况要考虑:
- 我们想要查找的值在尾部。
- 我们想要查找的值在树里面。
这里就是我们需要使用到尾部偏移量的地方。查找过程写成伪代码看起来是这样:
if lookup_index < tail_offset: # tree_lookup = old lookup technique return tree_lookup(lookup_index) else: return tail[lookup_index - tail_offset]因为我们知道尾部偏移量就是元素在树里的总量,我们仅仅需要检查待查找的元素是否比尾部偏移量小。如果是,我们就执行『老的』查找过程,否则,我们知道它在尾部。在那种情况下,我们把索引减去尾部偏移量(这就是我们称之为偏移量的原因),然后使用计算得来的新的索引位置到尾部里查找。
更新
跟查找的实现类似,更新也跟原来的更新实现非常相似。唯一的区别发生在你想更新的值就在尾部里面。再次有两种情况:一是你要更新的值在树里面,另一个就是你要更新的是尾部。
if update_index < tail_offset: # tree_update is the old update technique return tree_update(update_index, elt) else: vector_copy = copy_head(this) vector_copy.tail = copy_tail(this.tail) vector_copy.tail[lookup_index - tail_offset] = elt return vector_copy首先,我们看下更新的元素在树里面的情况。我们仍然以 Part 1 里的老例子为例,更新索引位置 5 的元素:
(def brown [0 1 2 3 4 5 6 7 8]) (def blue (assoc brown 5 'beef)) 这可以得到下面这棵树:
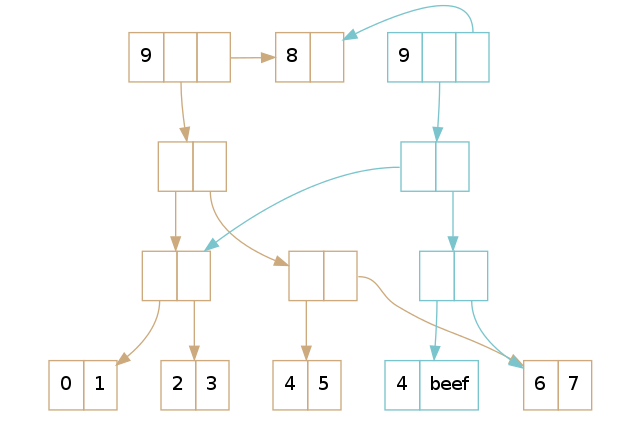
正如 Part 1 所解释的那样,我们做了路径拷贝并替换叶子节点上的元素。但是呢,注意到它们共享了尾部:毕竟,它没有变动,因此为什么要费心去拷贝它呢?
第二种情形是我们要修改的元素在尾部。让我们重用前面的例子,但是将索引位置修改 8:
(def brown [0 1 2 3 4 5 6 7 8]) (def blue (assoc brown 8 'beef)) 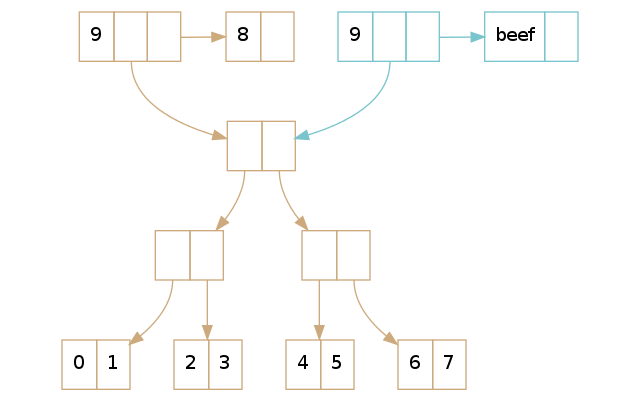
这次看到我们拷贝了 vector 的『头部』和尾部,然后在它上面执行了修改操作。因为我们对树没有做任何修改,我们就可以和没有修改之前的 vector 共享树的部分。这个操作的耗时就是常量的,不是 近乎 常量级的。
插入
查找和更新都很简单,但是如果我们查看下插入和删除呢?没错,结果是它们也同样不难。对于插入来说,我们再次有两种情形要考虑,但是这次有一点点不同:
- 在尾部有足够空间。
- 在尾部没有空间了。
第一种情况非常容易:拷贝下尾部,在它的末尾插入新元素。这篇博客的第一幅图刚好就展示了它是如何工作的。但是当尾部没有足够空间的时候我们应该怎么办?
原理和 Part 1 描述的插入过程很像,但是有一点小修改:不再是插入一个单一的值,替代地,我们插入一个叶子节点。回想下,尾部就是一个叶子节点,被 vector 的根节点直接指向。
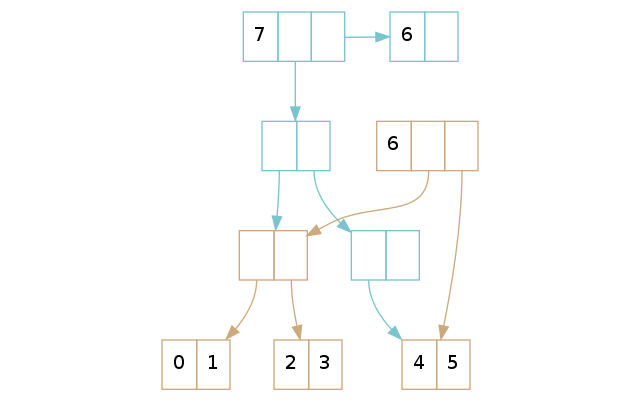
在上面的示例里,褐色 vector 的尾部已经满了:你没法往尾部插入更多的元素了。一个 conj 操作将创建蓝色的 vector,在那里面我们了解到我们必须将尾部本身插入树中。按照 Part 1 的规则,我们将尾部放入树里面,然后创建一个新的尾部用来存放新元素。
实际上,插入本身不需要更多解释了,并不难理解和掌握它。但是当一个实际的 vector 实现做插入的时候,需要特别小心处理索引。幸运地是,实现过程中需要面对的最大困难是所谓大小差一的错误(off-by-one error,译者注:也就是数组索引位置处理不当,通常在边界的时候多处理或者少处理了一个元素)。
删除
当处理删除的时候,我们面临一个设计上的抉择:某些情况下,我们不得不把叶子节点向上移动作为尾部。但是什么时候应该这样做呢?我们应该在 vector 里保留空的尾部吗?并且只有在对一个尾部已经为空的 vector 执行出队操作的时候才去向上移动叶子节点吗?或者,我们总是保留一个非空的尾部在 vector 中?
结果证明至少有两个理由要求我们保证在所有情况下尾部为空:最显而易见的理由是你现在能够保证 peek 操作一定是常量时间的。另一个不那么明显的理由是随机查找,平均来说将更快:如果在尾部查找一个元素比在树里查找耗时更短,那么更好的是让尾部保持『满』的状态,而不是一个空的尾部。
因此,我们以 —— 你可能猜到了 —— 两种不同的情况处理来结束讨论:
- 在尾部,我们拥有多于一个的元素。
- 在尾部,我们只有一个元素。
正如我刚才提到的,不会有任何 vector 会在尾部没有元素(除了空的 vector 这种异常情况)。假设尾部至少有一个元素在完全没有问题的。
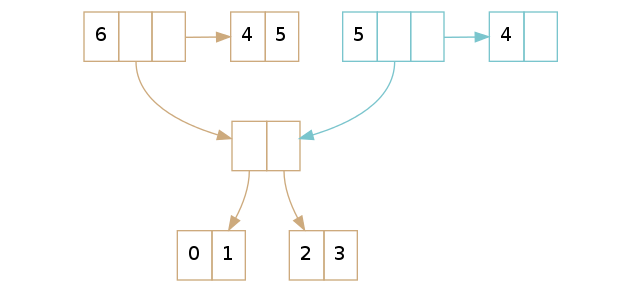
如果在尾部我们有多于一个的元素,我们只需要拷贝这个尾部,删除它的最后一个元素,然后返回新的 vector。上面的例子显示给我们只有尾部不同,正是我们预期的那样。
请记住如果我们对同一个 Persistent Vector 做两次出队操作,我们将创建两个尾部,尽管它们的内容是一样的:
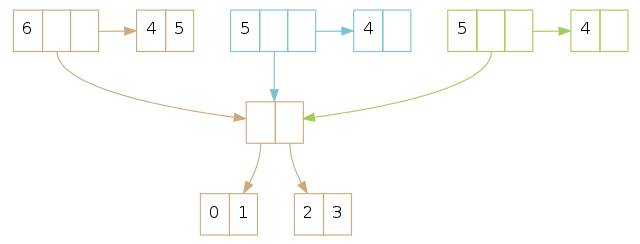
如果我们在尾部只有一个元素,我们需要将树中的最右叶子节点『提升』为新的尾部,还要将它(译者注:最右叶子节点)从树上移除。这些步骤跟在没有尾部的 vector 执行查找和出队一个元素的操作相似,只是将查找和删除元素替换为查找和删除叶子节点。
最复杂的例子出现在你需要删除空的节点并干掉根节点,就像 Part1 描述的那样。但是,如果你按照 Part 1那里介绍的规则行事,并且将叶子节点当做『元素』,你会觉的还好处理。下面就是这么个例子,把最右叶子节点『提升』为根节点。
Next Up
这个系列的 下一篇 将解析 transient:我们为什么需要它们,以及它们的工作原理。最终这个系列博客的最后一篇博客将包含 ArrayList 和 Persistent Vector 的性能对比。
[1] 持有非空尾部的有没有什么不利的地方?从理论角度出发,空的 vector 将更多是一种边缘情况,因为它不符合这个规则(译者注:指尾部非空)。但是从实践角度出发,这没有关系。空的 vector 本来就是一种特殊情况,因此采用这个设计后,实现本身并不会更复杂。











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

