转载

翻译：字母排序算法解析

简介

假设存在数组（如：[0, 3, 3, 5, 8]），现在要生成其所有排列，最好的方法是什么？

可以按序，从数组中选取第1个元素将其作为首个元素，再用剩余元素递归地作类似排序，依次类推，就能得到所有的排列组合。但这种方法实现起来并不简单，整个过程包含了递归，栈存储，还得跳过重复的组合。再者，如果条件不允许使用额外的存储，只能对原数组元素进行处理，过程就更困难了。

针对这种情况，生成全排列组合最优的办法就是按组合的顺序，从低到高，先生成低的，再变换该排列组合，生成下一顺序的组合。而本文要描述的就是这种序列生成算法。接下来就一步步举例说明该算法。

算法详情

我们使用数组[0, 1, 2, 5, 3, 3, 0]举例说明。

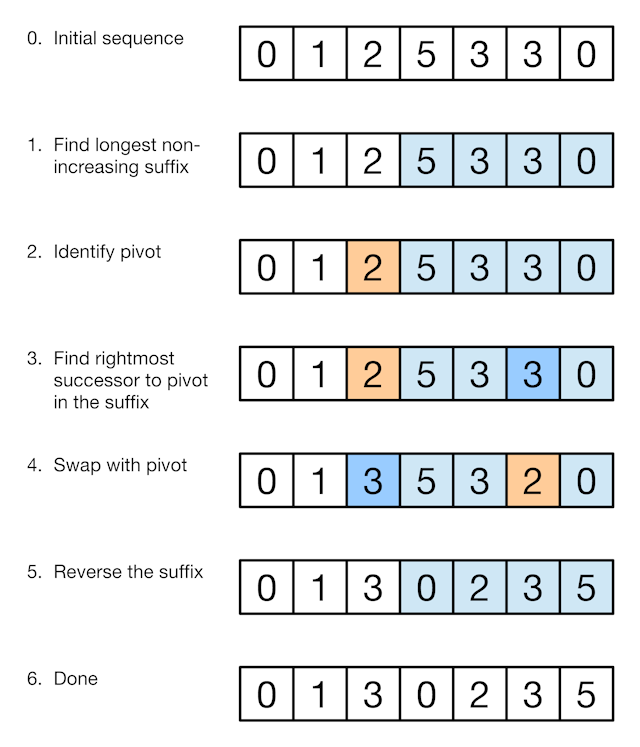
翻译：字母排序算法解析

算法的关键点在于我们已经有了一个排列组合了，而现在需要计算 下一个排列组合 ，所以要 尽可能小地提升 当前排列组合的序列。这个过程和数数一样，我们尽量保持当前排列组合左边不动，只调整最右边的数字。

比如，从左到右看数组，不用将最左边第1个数0变成1（结果为[1, 0, 2, 5, 3, 3, 0]），因为相比之下，如果将[0, 1]变成[0, 2]（结果为[0, 2, 1, 5, 3, 3, 0]）更接近“下一个排列组合”。实际上其实这么变也不是最优的结果，接下来就说明到底该怎么做才是正确的。

首先、获取当前排列组合 最长的非递增后缀 ，本例中，这个后缀是[5, 3, 3, 0]。单看这个后缀，其排列组合顺序在其所有组合中已经是最高的了，所以无论怎么调整其顺序，都无法再获取更高排序的组合了，所以我们只能变换其左边的数字。（要识别出后缀，只需要从右到左遍历序列，时间复杂度为O(n)。且该后缀至少要包含一个元素，因为单个元素可以视作非递增的序列。）

接着、现在可以知道后缀左边第1个元素（本例中该元素为2），我们将其称为哨兵（如果后缀左边没有元素，即当前排列组就是从大到小排列的，则说明当前排列组合已经是最大的）。因为哨兵的值必小于后缀的首个元素（本例中后缀首个元素为5），而后缀是从大到小排列的，所以会有一部分元素比哨兵大。现在找到后缀中比哨兵大的最小元素，将哨兵和该元素交换位置，则前缀（这里将后缀左侧的排列称为前缀）就是最小值，本例中，新前缀为[0, 1, 3]，新后缀为[5, 3, 2, 0]（如果后缀中要和哨兵换位置的元素有很多个，我们应该取最右边的那个来交换）。

最后、现在将新后缀重新排列，使其元素从小到大排列。之所以要这样，是因为我们调整了前缀，将其变大了，所以后缀就要尽可能小。因为新后缀本来就是从大到小排列的，现在要将变为从小到大排列，直接逆序即可得到结果。现在我们可以拿到下一个序列的排列组合，为[0, 1, 3, 0, 2, 3, 5]。

算法总结如下：