【译】我从用 JavaScript 写斐波那契生成器中学到的令人惊讶的 7 件事

生成器（generator）函数是 ES6 的新特性。为了更加深入研究它，我决定写一个斐波那契数列的生成器函数。

以下是我所学到的。

采用新特性

有时候，当一个新的语言特性出现，我就毫不犹豫地开始全面使用它。在 ES6 的一些新特性上就是这种情况。我将最喜欢的 ES6 特性列在一个清单里，我把它们称为 the ROAD MAP ：

• R Rest 和 Spread
• O 对象字面量简写 (Object Literal Shortcuts)
• A 箭头函数 (Arrow Functions)
• D 解构和默认参数 (Destructuring & Default Parameters)
• —
• M 模块 (Modules)
• AP 异步编程 (Asynchronous Programming: promises & generators)

当我列出这个清单的时候，我原以为这些是我最常使用的 ES6 特性。最初，我对能使用生成器感到非常兴奋，但是现在，当我已经使用过它们一段时间之后，在我真实的应用代码中并没有找到许多使用生成器的好的应用场景。而对大多数我可能要使用生成器的场景，我使用 RxJS 替代，因为它有更丰富的 API。

这并不意味着生成器就没有多少好的应用场景。我对自己说，在我真正为它们疯狂之前，我还得等待更好的 JS 引擎支持，但也可能是我根本就没有用生成器的思维来思考，所以才用不好它。最好的解决办法是去积累更多关于生成器的实践。

当我一听说生成器的时候，一个用处马上出现在我的脑海里，那就是我们可以使用它来从任意一个无穷级数里得到值。这可能有许多应用场景，例如图形的生成算法、电脑游戏等级、音乐序列，等等……

斐波那契数列是什么？

斐波那契数列是一个简单的、形式规范的例子，大多数读者可能已经对它比较熟悉。以下是它的基本概念：

斐波那契数列是以下一系列数字：

0, 1, 1, 2, 3, 5, 8, 13, 21, 34…

在种子数字 0 和 1 之后，后续的每一个数字都是前面两个数字之和。斐波那契数列的一个有趣的性质是，数列的当前数字与前一个数字的比值无限趋近于黄金分割数， 1.61803398875…

你可以使用斐波那契数列来生成各种各样有趣的东西，比如黄金螺旋 (Golden Spiral)，自然界中存在许多黄金螺旋。

生成器函数是什么？

生成器函数是 ES6 的新特性，它允许一个函数 随着时间生成许多值 。生成器函数返回一个对象，这个对象可以被迭代，它的每一次迭代从生成器函数中拉取一个值。

当生成器函数被调用，不同于普通函数直接返回一个值，它返回一个迭代器对象。

迭代器协议

迭代器对象拥有一个 .next() 方法。当 .next() 方法被调用时，生成器函数体从它上一次执行 .next() 之处恢复。它继续执行直到遇到一个 yield ，之后它返回如下对象：

{   value: Any,   done: Boolean } 

value 属性包含一个被 yield 的值， done 标志表明生成器是否已经 yield 到了最后一个值。

迭代器协议（iterator protocol）被使用在 JavaScript 的许多地方，包括新的 for...of 循环、数组的 res/spread 操作符，等等。

1. 生成器与递归不同

我习惯于担心 JavaScript 的递归调用。当一个函数调用另一个函数，一个新的堆栈帧 (stack frame) 被分配用来保存函数的数据状态。无限递归会导致内存问题，因为堆栈帧的分配有一个上限。如果你的调用达到了可分配的上限，它将会导致堆栈溢出。

堆栈溢出就像是警察突袭你的派对，告诉你所有的朋友赶紧回家。一切都毁了。

当 ES6 引入尾调用优化时，我感到非常兴奋，因为它能让一个递归函数在每一次迭代中复用同一个堆栈，但是它只对递归调用在尾部时有效。一个调用在尾部的意思是函数返回的递归调用结果不再参与任何进一步的计算。

棒极了！我的第一版简单实现直接使用形式规范的斐波那契数列数学递推定义：

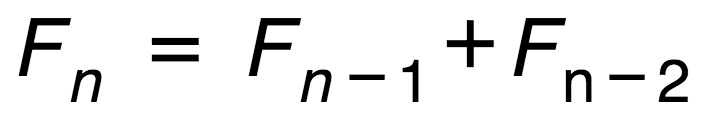
使用种子值 0 和 1 来开始序列，将变化递归写入函数调用签名，它看起来如下：

function* fib (n, current = 0, next = 1) {   if (n === 0) {     return 0;   }    yield current;   yield* fib(n - 1, next, current + next); } 

我很高兴它看起来那么的简洁。种子值被明显地写在函数签名里，而斐波那契数列的递推公式在递归调用中被非常清晰地表达。

if 条件当 n 为 0 时，通过使用 return 代替 yield 让循环终止。如果你不传 n ，它的值为 undefined ，于是 n - 1 变成 NaN ，结果是生成器函数将永远不会终止。

这个实现非常直接…… 而且幼稚。当我想要测试非常大的值时，它崩溃了。

(ಥ﹏ಥ)

悲催， 尾调用优化对生成器无效 （因为尾调用优化这个 ES6 特性有争议，现在大部分浏览器和默认的 Node.js 环境下对普通函数调用也无效啊——译者注）。根据规范“函数调用 运行时语义：求值 ”这一段：

IsInTailPosition 对生成器返回 false。 (看 14.6.1 ):

换句话说，我们 要避免对无限生成器使用递归 。如果你想避免堆栈溢出，你需要用迭代形式代替递归形式。

做一点小改动，我们可以用迭代形式将递归替换掉：

function* fib (n) {   const isInfinite = n === undefined;   let current = 0;   let next = 1;    while (isInfinite || n--) {     yield current;     [current, next] = [next, current + next];   } } 

如你所见，我们依然用同样的变量交换。但与之前在函数调用签名里交换不同，这一次我们使用解构赋值，在 while 循环里完成交换。我们在生成器里定义 isInfinite ，以便实现无限生成。

2. 使用参数限制迭代次数

我们可以通过你的生成器结合解构赋值和 ...rest 语法得到一个结果数组：

const [...arr] = generator(8); 

但是如果你的生成器是一个无限的序列，无法根据传参设置个数限制，那么结果数组就会被无限填充。

┻━┻ ︵ヽ(`Д´)ﾉ︵ ┻━┻

在上面的两个斐波那契实现版本里，我们都允许调用者传一个 n 值，限制数列只产生前 n 个数值。看起来很好！

┬─┬ ノ( ゜-゜ノ)

3. 注意使用缓存函数（Memoized Function）

对于斐波那契数列之类的计算，将结果缓存下来十分诱人，因为这么做可以显著地降低需要的迭代次数。换句话说，这能让计算变快许多。

什么是缓存函数？

对于给定同样的参数总是返回同样的值的函数，你可以在缓存中记录下计算结果，以便于将来调用的时候不用再重新算一遍结果。用同样的参数调用的时候，结果直接从缓存中查询来返回，而不用再重复计算。斐波那契算法重复了许多次计算来获得结果，这意味着如果我们缓存计算结果，我们可以节省许多时间。

让我们看一下我们如何能从斐波那契生成器中缓存迭代结果：

const memo = [];  const fib = (n) => {   if (memo[n] !== undefined) return memo[n];    let current = 0;   let next = 1;    for (let i = 0; i < n; i++) {     memo[i] = current;     [current, next] = [next, current + next];   }    return current; };  function* gen (n = 79) {   fib(n);   //此处应该是  yield* memo.slice(0, n)？——译者注   yield* memo.slice(0, n + 1); }  export default gen; 

由于 n 本质上代表一个数组中数值的索引，我们可以使用它作为数组字面量的索引。第一次计算之后，后续的调用将查找索引返回相关的结果值。

修改：

上面代码我做了修改，原版代码有一处 bug。第一次运行函数，一切都正确，但是缓存被写错了，因为当缓存命中的时候你不能仅仅 yield 一个值，不同于 return ， yield 并不会停止函数的剩余部分运行，它仅仅只是暂停执行直到 .next() 再一次被调用。

这对我来说是最难点，它让我脑袋迷糊了。 yield 并不仅仅只是 return 了生成器。你也需要仔细考虑通过 next() 继续你的函数执行为你写逻辑的方式带来了怎样的影响。

在这个例子里，我能够用 yield 让逻辑正确运行，但是它使得控制流变得难以读懂。

它让我想到了一个缓存内容的方式，如果我将生成器函数从计算逻辑中分离出来，那么代码就会变得易懂一些。

如你所见，新的生成器函数非常简单——它仅仅通过调用缓存函数 fib() 计算缓存数组，然后代理给生成器使用 yield* 产生结果数组。

yield* 是 yield 的一个特殊形式，它可以代理给另一个生成器或者可迭代对象。例如：

const a = [1, 2, 3]; const b = [4, 5, 6];  function* c () {   yield 7;   yield 8;   yield 9; }  function* gen () {   yield* a;   yield* b;   yield* c();   yield 10; }  const [...sequence] = gen(); console.log(sequence); // [1,2,3,4,5,6,7,8,9,10] 

性能测试 (Benchmarks)

无论何时我研究不同的算法实现，我通常写一个简单的 benchmark 脚本来比较它们的性能。

为了进行测试，我用每个算法生成 79 个数字。我是用 Node 的 process.hrtime() 为每个实现记录精确到纳秒的时间，我让每个实现运行三次，计算平均结果：

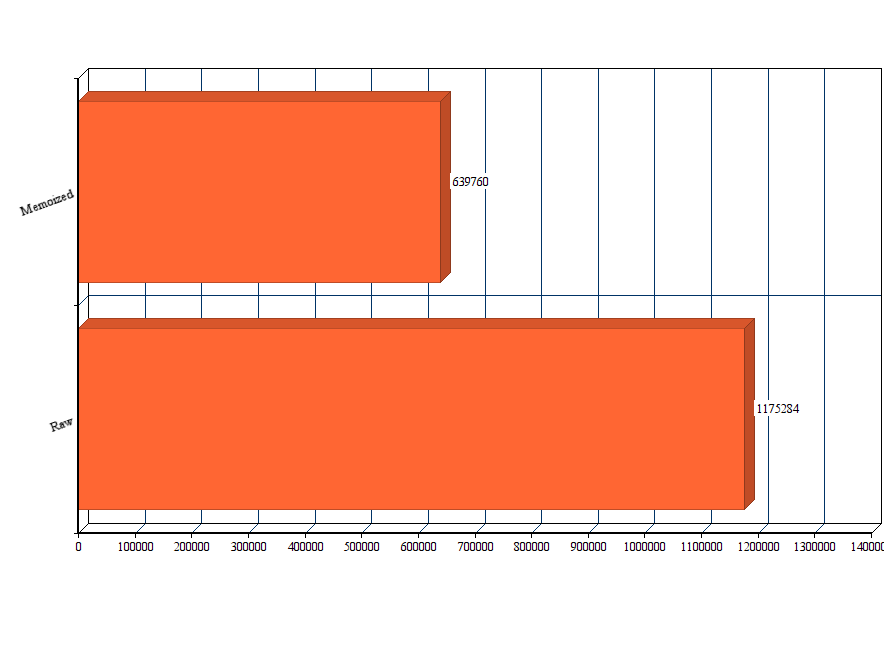
如你所见，性能有明显的不同。如果你要生成许多数值，并且你希望它能快一些，缓存的版本明显是更好的选择。

还有一个问题：如果是一个无穷数列，缓存数组将无限制地增长。最终，你将会用尽堆内存，而这将导致 JS 引擎崩溃。

然而别太担心。对于斐波那契数列，你会先遇到 JavaScript 最大整数精度问题，JavaScript 所能精确表示的最大整数为 9007199254740991 。这个数超过 900 万亿，是一个很大的数，但是对斐波那契数列来说不算什么。斐波那契数列增长的非常 快 ，你生成数列的 79 个项之后就会遇到那个问题了。

4. JavaScript 需要一个内置的 API 来精确计时

每次我写一个简单的性能测试脚本，我希望能有一个精确计时的 API，它在浏览器和 Node 下都可用，可惜没有这样的 API。我们所能得到的最接近需求的选择是用一个库提供同时提供对浏览器的 performance.now() 和 Node 的 process.hrtime() 两个 API 的统一封装。不过实际上，Node 的性能测试已经足够了。

我唯一的不满是 Node 的 process.hrtime() 返回一个数组，而不是直接返回一个纳秒数值。不过这很容易修正：

const nsTime = (hrtime) => hrtime[0] * 1e9 + hrtime[1]; 

只需要将 process.hrtime() 返回的数组传给这个函数，然后你就能获得简单的纳秒值了。让我们看一下我用来比较迭代版和缓存版的斐波那契数列生成器的性能测试脚本。

import iterativefib from "iterativefib"; import memofib from "memofib"; import range from "test/helpers/range";  const nsTime = (hrtime) => hrtime[0] * 1e9 + hrtime[1];  const profile = () => {   const numbers = 79;   const msg = `Profile with ${ numbers } numbers`;    const fibGen = iterativefib();   const fibStart = process.hrtime();   range(1, numbers).map(() => fibGen.next().value);   const fibDiff = process.hrtime(fibStart);    const memoGen = memofib();   const memoStart = process.hrtime();   range(1, numbers).map(() => memoGen.next().value);   const memoDiff = process.hrtime(memoStart);    const original = nsTime(fibDiff);   const memoized = nsTime(memoDiff);    console.log(msg);   console.log(`     original: ${ original }ns     memoized: ${ memoized }ns   `); };  profile(); 

hrtime() 里我最喜欢的特性是你可以传递开始时间进去获得从开始时间到当前经过的时间段——这正是性能测试所需要的。

有时候，进程在操作系统的任务调度中会碰上坏运气，所以我喜欢运行脚本多次，然后取平均值。

我确信你可以用更精确的方法来对你的代码性能测试，但是大多数情况下像这样测试已经足够好了——尤其是像缓存版斐波那契实现这样已经足够明显比前一个版本要好了。

5. 当心浮点数精度问题

我不想用太多疯狂的数学来烦你，但你知道有一个非常高效的方法来计算斐波那契数列，而根本不用迭代或者递归吗？它看起来像这样：

const sqrt = Math.sqrt; const pow = Math.pow;  const fibCalc = n => Math.round(   (1 / sqrt(5)) *   (     pow(((1 + sqrt(5)) / 2), n) -     pow(((1 - sqrt(5)) / 2), n)   ) ); 

唯一的问题是浮点数精度限制。原本的公式中不包含四舍五入，我把它加上了，因为浮点数错误导致结果从 n = 11 之后开始产生偏差。这并不是什么严重问题。

好消息是添加了四舍五入之后，我们可以保持精度直到 n = 75 。 好多了。 只有 75 之后的部分数值遇到 JavaScript 原生 Number 类型的最大精度问题，如我们之前 n = 79 时发现的那样。（因为 pow(((1 + sqrt(5)) / 2), n) 比较大，先超过了最大精度，所以这个方法只能计算到 75 ——译者注）

因此，如果我们不要求超过 n = 75 之后的值，这个快速的公式能很好地工作。让我们将它变成生成器：

const sqrt = Math.sqrt; const pow = Math.pow;  const fibCalc = n => Math.round(   (1 / sqrt(5)) *   (     pow(((1 + sqrt(5)) / 2), n) -     pow(((1 - sqrt(5)) / 2), n)   ) );  function* fib (n) {   const isInfinite = n === undefined;   let current = 0;    while (isInfinite || n--) {     yield fibCalc(current);     current++;   } } 

看起来不错。让我们看一下性能测试结果：

Profile with 79 numbers     original: 901643ns     memoized: 544423ns     formula:  311068ns 

是的，更快，但是我们失去了最后几个精确数值，这个代价值得吗？

¯(º_o)/¯

6. 了解你的极限

在我开始之前：

• 我不知道使用标准的 JavaScript Number 类型可以从这个数列中获得多少精确值。
• 我不知道从公式版的实现中可以获得多少精确值。
• 我不知道需要多少层递归调用来获得这些精确值。

但我现在知道所有的这些极限了，最好的实现版本是目前我还没有展示给你的，如下：

const lookup = [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170, 1836311903, 2971215073, 4807526976, 7778742049, 12586269025, 20365011074, 32951280099, 53316291173, 86267571272, 139583862445, 225851433717, 365435296162, 591286729879, 956722026041, 1548008755920, 2504730781961, 4052739537881, 6557470319842, 10610209857723, 17167680177565, 27777890035288, 44945570212853, 72723460248141, 117669030460994, 190392490709135, 308061521170129, 498454011879264, 806515533049393, 1304969544928657, 2111485077978050, 3416454622906707, 5527939700884757, 8944394323791464];  function* fib (n = 79) {   if (n > 79) throw new Error("Values are not available for n > 79.");   yield* lookup.slice(0, n); } 

大多数时间，当我在一个实际应用中使用无穷级数，我实际上需要的是一组有限的数值，为了一个特定的目的（通常是生成图片）。大多数时间，从一个 查找表 里获取值比去计算一个值要来得快。事实上，这是 80 年代和 90 年代的计算机游戏开发中一种常用的优化方法，也许直到现在仍然是。

由于数组在 ES6 中是可迭代的并且已经有生成器那样的默认行为，我们可以在生成器函数中简单通过 yield* 来代理查找表。

好不奇怪，这是最快的实现方法，远远甩开其他方式：

Profile with 79 numbers     original: 890088ns     memoized: 366415ns     formula:  309792ns     lookup:   191683ns 

回顾前面，我很肯定只要我们限定数列只包含精确值，调用栈不会有问题…… 一个稍微修改过的递归版本也能做得很好：

const memo = [0, 1];  const fib = (n) =>   memo[n] !== undefined ? memo[n] :   memo[n] = fib(n - 1) + fib(n - 2);  function* gen (n = 79) {   if (n > 79) throw new Error("Accurate values are not available for n > 79.");   fib(n);   yield* memo.slice(0, n); }  export default gen; 

这是我最喜欢的一个版本，种子值可以放在缓存里，让实际计算尽可能接近数学递推关系： Fn = Fn-1 + Fn-2

在生成器里，我们只是再一次代理缓存数组。

注意极限

• 如果你使用浮点数学公式，你应该要明确测试其精度范围。
• 如果你使用一个数列，这个数列以指数方式增长，你需要算出在 JS 的 Number 类型限制下你可以生成多少个数值。
• 如果你的极限足够小，考虑预生成一个查找表来加速你的应用。

如果你决定需要比 JavaScript 原生能提供的更大精度范围的数值，也不是完全不行。有支持任意大小的整数库存在，例如 BigInteger 。

7. 许多对象如生成器一样

当生成器函数被引入 ES6，许多其他的内置对象也实现了 迭代器协议 （由生成器返回的，可被迭代执行的对象）。

更准确地说，它们实现了 可迭代协议 （iterable protocol）。 String 、 Array 、 TypedArray 、 Map 以及 Set 都是内置的可迭代对象，这意味着它们都有一个 [Symbol.iterator] 属性，这个属性不可被枚举。

换句话说，你可以使用迭代器 .next() 方法迭代任意类数组的内置对象。

下面的代码演示如何访问数组迭代器。同样的技术适用于任何实现了可迭代协议的对象：

let arr = [1,2,3]; let foo = arr[Symbol.iterator]();  arr.forEach(() => console.log( foo.next() )); console.log(foo.next()); // { value: 1, done: false } // { value: 2, done: false } // { value: 3, done: false } // { value: undefined, done: true } 

You can even build your own custom iterables:

const countToThree = {   a: 1,   b: 2,   c: 3 };  countToThree[Symbol.iterator] = function* () {   const keys = Object.keys(this);   const length = keys.length;    for (const key in this) {     yield this[key];   } };  let [...three] = countToThree; console.log(three); // [ 1, 2, 3 ] 

甚至重定义内置可迭代行为也是可以的，但是注意——我发现 Babel 和 V8 存在不一致的行为：

const abc = [1,2,3];  abc[Symbol.iterator] = function* () {   yield "a";   yield "b";   yield "c"; };  let [...output] = abc; console.log(output); abc.forEach(c => console.log(c));  // babel logs: /* [1,2,3] 1 2 3 */  // Node logs: /* [ "a", "b", "c" ] 1 2 3 */ 

我想可能写一个函数将数组转成迭代器比直接使用 arr[Symbol.iterator]() 要方便，因此我写了一个，并且我还让它支持了有趣的 sllicing API，这样你可以很容易得到数组的一部分并将它转成迭代器。我把它叫做 arraygen。你可以 在 GitHub 上浏览 arraygen 。

结论

希望我提到了一些你可能还不知道的关于生成器的内容。我也提到了几个由研究生成器引申出来的内容：

1. 避免递归。 生成器没有实现尾调用优化。
2. 允许参数限制你的生成器长度 ，这样你可以使用 ...rest 操作符来解构它们。
3. 缓存无限生成器会超出堆内存上线。
4. JavaScript 有两个完全不同的精确计时的 API。 为什么不能统一起来？(ಥ﹏ಥ)
5. 浮点数精度问题会破坏基于公式的无限生成器。 要当心。
6. 了解你的极限。 你的生成器是否有足够的空间来满足你的应用需求？在这个空间里它获取的值是否足够精确？你是否将遇到你使用的数据类型的限制？JS 引擎是否有足够的内存来支持你的生成器运行直到你得到满意的结果？
7. 大部分内置对象的行为有点像生成器 ，通过可迭代协议，你可以定义你自己的可迭代对象。

如果你想要进一步研究斐波那契数列的例子，你可以 从 GitHub 上克隆完整代码 。