转载

一文告诉你机器学习中进行模型评价、模型选择和算法选择的终极方法（PART I）

本文为数盟原创译文，转载请注明出处为“数盟社区”。

by Sebastian Raschka

引言

机器学习已经成为我们生活中的一部分，对购买者、消费者或是希望进行研究和实践者都很重要！无论我们应用预测建模技术来进行我们的研究还是解决业务问题，我相信有一个共同点：我们要做“好”的预测！诚然，我们需要训练数据模型，但是我们怎么知道它能很好的在看不见的数据中运行？我们怎么避免它仅仅记忆那些我们提供的数据，却未能对我们从未见过的样本作出良好的预测？我们如何优先选择一个好的模型？也许一个不同的学习算法，可以更好地适用于解决手头的问题。

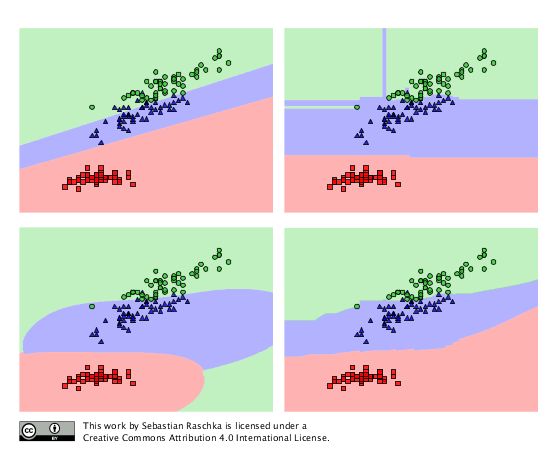
模型评估，当然不是我们机器学习管道的终点。在我们处理任何数据之前，我们要提前制定计划，并使用适合我们的目的的技术。在这篇文章中，我们对这些技术进行选择，我们将看到它们如何适应更大的格局——一个典型的机器学习工作流程。

性能评估：泛化性能VS模型选择

让我们以一个简单的问答来开始这个部分吧：

问：“我们如何评估机器学习模型的性能？”

答：“首先，我们把训练数据提供给我们的学习算法来学习一个模型。第二，我们预测我们的测试标签。第三，我们计算在测试数据集中的错误的预测数量来计算模型的错误率。

没那么简单！不幸的是，就我们的目标而言，估计模型的性能是没那么容易的。也许我们应该从另一个角度来解决这个问题：“为什么我们关心性能评估？”理想情况下，一个模型的性能评估会告诉我们看不见的数据有多好的表现，在机器学习的应用或开发新的算法中对未来数据的预测往往是我们要解决的主要问题。通常情况下，机器学习中涉及到大量的实验，虽然-例如，学习算法的内部参数的调整，所谓的超。在不同的超参数设置训练数据集上运行的学习算法会得出不同的模型。因为我们通常有兴趣从这个集合中选择最佳的执行模型，我们需要找到一种方法来估计它们的各自的性能，以便对彼此进行排序。一步超越单纯的算法微调，我们通常不只是试验一个单一的算法，我们认为将是“最佳的解决方案”，在特定情况下。更多的往往不是我们想要比较不同算法的，而是在预测和计算性能方面。

让我们来总结一下为什么我们要评估模型的预测性能：

我们要估计的泛化误差，我们的模型对未来的预测性能（看不见）的数据。

我们要通过调整学习算法，从一个给定的假设空间选择表现最好的模型来提高预测性能。

我们要识别的机器学习算法，是最适合用于解决问题的。因此，我们要比较不同的算法，选择最佳的执行一个以及最佳的执行模型的算法的假设空间。

虽然上面列出的三个子任务都很普通，但我们要估计一个模型的性能，它们都需要不同的方法。我们在这篇文章中将讨论一些不同的方法来解决这些子任务。

当然，我们要尽可能准确地估计未来的表现。然而，如果有一个关键的信息从本文中，它是有偏见的性能估计是完全可以在模型选择和算法的选择，如果偏置影响所有模型同样。如果我们为了选择最佳的执行一个不同的模型或算法，我们只需要知道的“相对”性能。例如，如果我们所有的性能估计是悲观的偏见，我们低估了他们的表演，10%，它不会影响排序。更具体地说，如果我们有三个模型的预测精度估计，如

M2: 75% > M1: 70% > M3: 65%,

如果我们增加了10%个悲观的偏见，我们仍然会对他们有同样的排名：

M2: 65% > M1: 60% > M3: 55%.

相反，如果我们将未来性能最好的排名模式（M2）报告为65%，这显然是相当不准确的。估计模型的真实性能可能是机器学习中最具挑战性的任务之一。

假设和术语

模型评估是一个复杂的话题。为了确保我们不会偏离核心信息，让我们做一些假设，并了解一些我们将在这篇文章中使用的某些技术术语。

i.i.d.

我们假设我们的样本是 i.i.d. （独立同分布），这意味着所有的样品已经从相同的概率分布，得出在统计上相互独立。不独立的情况下，将与时间数据或时间序列数据。

监督学习与分类

本文将重点聚焦于机器学习的一个子类——监督学习，其中我们的目标值从我们提供的数据中知晓。虽然许多概念也适用于回归分析，我们将重点放在分类，分类目标标签的样本。

0-1 损失和预测精度

在下面的文章中，我们将重点放在预测的准确性，这被定义为所有正确的预测数量除以样品的数量。有时候，我也会用“错误”，因为“泛化误差”听起来比“泛化精度”自然。我们计算预测误差1-准确性或不正确的预测由样本数量n所得的值。用更正式的术语表述，我们定义0-1损失为L(⋅)

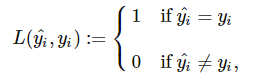一文告诉你机器学习中进行模型评价、模型选择和算法选择的终极方法（PART I）其中， yi 是第i个真正的类标签和yi^第i类预测标签。然后，我们计算的精度平均0-1损失数据集中S中所有N个样本：

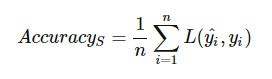
一文告诉你机器学习中进行模型评价、模型选择和算法选择的终极方法（PART I）

偏差

当我们在本文中使用术语偏差的时候，我们指的是统计学中的偏差（在机器学习系统中相反）。一般来说，一个估计β^^β的偏差是其预期值E之间[β^] E [β^]和参数的β被估计真值的差异。

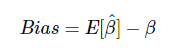
一文告诉你机器学习中进行模型评价、模型选择和算法选择的终极方法（PART I）

方差

方差就是估计值β和它的期望值E[β^]的统计差异。

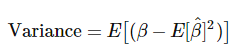
一文告诉你机器学习中进行模型评价、模型选择和算法选择的终极方法（PART I）

如果我们以小的训练集波动多次重复学习过程，方差是我们的模型预测的可变性的度量。模型构建过程是对这些波动越敏感，方差越高。

最后，让我们对模型，假设，分类，学习算法和参数等概念进行定义：

目标函数：在预测模型中，我们通常是模拟特定的进程有兴趣的;我们要学习或近似一个具体的，未知的功能。目标函数f（x）= YF（x）= y是真正的函数f（⋅）F（⋅），我们要建模。

假设：一个假设是有一定的作用，我们认为（或希望）类似于真正的功能，我们要建模的目标函数。在垃圾邮件分类上下文，这将是我们想出了，使我们能够从非垃圾邮件的垃圾分开分类规则。

模型：在机器学习领域，术语假说和模型通常可以互换使用。在其他学科，也可以有不同的含义：一个假设可能是“猜测”，由科学家，该模型将是这样的猜测，以检验这一假设的表现。

学习算法：同样，我们的目标是找到或近似目标函数，和学习算法是一组指令，它试图通过我们的训练集的目标函数来建模。学习算法配备了一个假设空间，该组可能的假设它探讨通过制定最终的假设未知目标函数模型。

分类：分类器是一个假设（现在，通常由机器学习算法学习）的一种特殊情况。分类器是一个假设的或离散值函数是，用于分配（分类）类标签特定数据点。在电子邮件分类为例，该分类可以用于标记的电子邮件为垃圾邮件和非垃圾邮件的一个假设。然而，一个假设必须不一定是同义的分类器。在不同的应用中，我们的假设可能是映射的学习时间和学生对他们的未来教育背景的函数，连续值，SAT成绩 – 连续的目标变量，适合回归分析。

超参数：超参数是一个机器学习算法的调谐参数 – 例如，一个L 2罚中的平均值的正规化强度的平方线性回归误差成本函数，或用于设定决策树的最大深度的值。与此相反，模型参数是一个学习算法适合于训练数据的参数 – 模型本身的参数。例如，一个线性回归线的权重系数（或斜率）和其偏置（或y轴截距）项是模型参数。

再置验证和截留方法

毫无疑问，截留方法是的最简单的模型评估技术。我们将我们的数据进行标记，并将其分为两部分：训练集和测试集。然后，我们拟合模型的训练数据和预测的试验组的标签。而正确预测的部分构成了我们的预测精度的估计 – 我们的预测中暂不当然真正的测试标签。我们真的不希望培养和相同的训练数据集评估我们的模型（这就是所谓的再置评估），因为这将由于过拟合而导致一个偏向乐观的结果。换句话说，我们不能告诉模型是否只是记忆训练数据与否，或者是否适用于新的、未知的数据。（在一个侧面说明，我们可以估算这个所谓的乐观偏差作为训练精度和测试精度之间的差）。

通常情况下，一个数据集为训练和测试集的分割是随机采样的一个简单的过程。我们假设我们的所有数据已经从具有相同的概率分布（相对于每一个类）绘制。我们随机选择这些样本为我们训练集〜2/3〜1/3中的标本。请注意这里的两个问题。

分层

我们必须牢记，我们的数据集表示从概率分布绘制的随机抽样;我们通常认为这个样本能够代表真正的人口 – 更多或更少。现在，无需更换进一步二次抽样改变样本的统计值（平均，比例，和方差）。频带分割无需更换影响的样本的统计信息的程度成反比样品的大小。让我们来看看使用虹膜数据集，随机分成2/3训练数据和1/3的测试数据为例：

（其源代码可以在这里 http://nbviewer.jupyter.org/url/sebastianraschka.com/ipynb/iris-random-dist.ipynb 找到）

就非分层随机的方式通常二次抽样是不是如果我们有比较大的，平衡的数据集的一个大问题。然而，在我看来，分层取样是在机器学习应用通常（只）是有益的。此外，分层抽样是非常容易实现的，Ron Kohavi提供了经验证据（1995 Kohavi）的分层对变化和k折交叉验证估计的偏差产生积极的影响，我们将在本文稍后讨论。

原文 http://dataunion.org/24543.html

正文到此结束