转载

趣味数据挖掘系列10：基因表达式编程

1 GEP的速度魅力在本系列之九的末尾提到，基因表达式编程GEP（Gene Expression Programming）是一种数据挖掘工具，是进化计算家族中较新的成员。在很多应用中，GEP比更传统的进化算法快2-4个数量级 ^[1,2,3] ；在实践中还发现，在某些特定场合，比传统方法快5-6个数量级，甚至更多。目前一些学校把GEP作为计算机专业及相关专业的硕博士选修课程。

GEP的速度魅力太吸引人了，12年前，关于GEP的简单信息在网上刚露头角，两周后，我们研究团队中，处于选题饥饿的博士生们读到了它，团队立刻跟踪研究，十多年来，得到过多个科学基金支持，至今还不疲不倦，无怨无悔，只因为它太奇妙，太快了。

为诠释这些稍难的内容，从过去的课程PPT中取了若干现成素材，任重而文短，作为科普博文，只能给出大致的轮廓。

2 GEP不是什么，又是什么GEP不是生物工程，不是生命科学。发明人Ferreira, Candida 把它称为Biologically Inspired Computing,（生物灵感激发的计算），它是一种数据挖掘的工具。在Candida的专著 ^[2] 中，第一章介绍了生物基因学的基本概念和常识，仅作它山之石，GEP借用了生命科学中基因，染色体等概念和进化的框架，作数据挖掘，用于发现公式、规则或规律。

GEP可以做什么？实践表明，非计算机专业的硕士生或博士生，经过几周或几个月的学习，可以用现成的GEP系统挖掘多种表达式（数学方程、公式，以及逻辑规则），从而也能挖掘逻辑规则表达的关联规则、分类规则、聚类规则等。例如发现太阳黑子规律，发现开普勒定律，设计门电路……,我们课题组还提出过一个新应用：作传统意义的因式分解，特别地，当给定多项式是质因式（在整数环上不可分解的多项式），如果强迫分解，也能做近似分解；表1给了一些示意，技术细节参见文献[4]。

输入：指定的或随机产生的测试函数	输出：GEP分解的结果多项式集
2x ⁶ -x ⁵ -5x ⁴ +8x ³ +1	2.00x ³ +3.00x ² –1.00x+1.00; 1.00x ³ -2.00x ² +1.00x+1.00
12x ⁷ +2x ⁶ +27x ⁵ +52x ⁴ +24x ³ +70x ² +39x+5	2.99x ² -1.00x+5.00; 4.00x ² +6.01x+0.98; 1.00x ³ -1.00x ² +1.99x+1.00
2x ¹⁰ +x ⁹ -x ⁸ +18x ⁷ -46x ⁶ +87x ⁵ -58x ⁴ +79x ³ -90x ² +34x-24	1.00x ² -2.01x+2.00;1.00x ³ -0.99x ² +3.00x-4 2.00x ² +0.98x+2.99; 1.02x ³ +3.00x ² +1.00

表1 用GEP作因式分解

GEP使用者的感觉 — 学当袁隆平。GEP的使用者的感觉就好像是动植物良种培育专家，好像在学当袁隆平，只不过培育的不是水稻，而是公式、规则和方程,良田就是真实、无噪声的（训练）数据；过程中有成功也有失败。失败了，修改方案或参数再来一次，被培育对象在电脑中进化，几秒钟进化几千代，几分钟，或几小时，进化几百万代; 实验室中没有严寒酷暑，不像袁隆平那样辛苦。

下面将比较GEP及其前辈算法GA（遗传算法 Genetic Algorithm）和 GP（遗传编程 Genetic Programming）；先说差别，后说共性。

3 差别在何处？编码有代沟。

GEP和与其前辈遗传算法（GA）和遗传编程（GP）的差别表现在遗传物质编码方式。上文用非编码形式介绍过公式 1 + x ⁴ 和 5 – x的杂交和变异，回忆相关要点：

杂交：对 1 + x ⁴ , 5 – x ，施加以换头术，交换红蓝部分，可以杂交出 5 + x ⁴ _， 1 -x；

变异：在染色体中插入、删除、或修改符号或符号片段。 6+x ⁷ 中的“+”变为“*”，得到 6*x ⁷ 。

3.1 遗传算法（GA）的编码—线性串，简单编码解决简单问题 GA直接把进化对象编码成0和1之称的线性串，表2 示意了公式编码以及杂交（换头术）：

公式	编码	杂交（交换前k位）k=6	杂交后，解码出的公式
1+x ⁴	1100101010	1011011010	5+x ⁴
-x	1011011110	1100101110	1 – x

表2 GA的编码，杂交和变异

GA编码简单，适合计算机处理，但语义不丰富。是简单编码解决简单问题。

3.2 遗传编程（GP）的编码 – 树结构，复杂编码解决复杂问题

GP把进化对象（例如公式）编码成树。为简单，图1 示意了二叉树，基本数据结构是节点三元组：（节点号，左儿子指针，右儿子指针）；通过指针适当地链接一组节点，组成从根节点开始的树。

图中语义多。理解有窍门：由下而上，逐步归约。例如：左边的黄色部分，从b开始，其父节点是开平方运算Sqrt，合起来表示 b ^1/2 ；类似地，右边黄色部分可由下而上归约，得到：（b/c）/a。

GP的杂交：例如，把左图和右图中的黄色部分交换。（像不像器官对移？）

GP的变异：例如，把左图中 a 突变为 x+y

与GA相比，GP采用了复杂的树结构，可以表达复杂的语义，是复杂编码解决复杂问题。

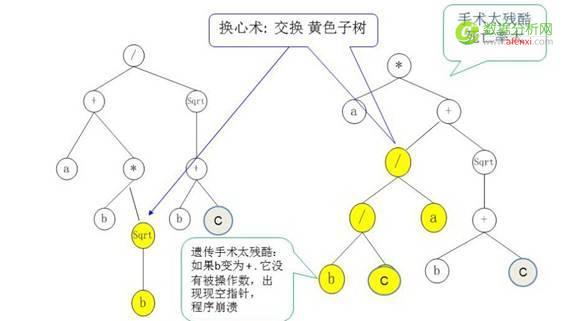
趣味数据挖掘系列10：基因表达式编程

图1，遗传编程GP的编码，杂交和变异

3.3 GA和GP编码的致命缺点-遗传手术下存活率低 GA和GP的遗传手术太残酷，杂交好像器官对换，变异中的插、删、改手术好像长瘤，截肢，器官移植，在这些很酷（Cool和残酷）的手术下，大多数对象都死亡或伤残了，浪费了计算机的时空资源。

3.4 GA和GP的爱情结晶：GEP

Candida Ferreira融合了遗传算法（GA）和遗传编程（GP）的优势，创造性地提出了基因表达式编程GEP。下图中给出了GA和GP杂交产生GEP的框架：

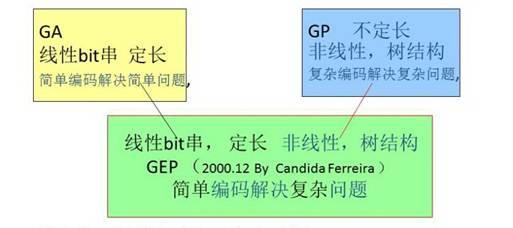
趣味数据挖掘系列10：基因表达式编程

图2 基因表达式编程 GEP继承了遗传算法GA和遗传编程GP的优势

GEP 继承了父亲GA的有刚性和规范，韬光养晦，藏复杂之树于简单之串，易作遗传操作，快速；

GEP 继承了母亲GP的柔性和多变多能，语义（感情）丰富；

GEP 向生物科学借鉴并实现了更多概念，如多基因染色体、如基因的表达、如中性区中隐形的继承和变异。最重要的是，GEP的巧妙编码使其成为不死鸟，在残酷的基因手术下能全部存活，这是GEP比GA,GP的速度普遍提高2-4个数量级的最重要原因。

其奇妙而简单的编码称为基因表达式，将在在第5节详细解析，现保留一点美好的悬念。

4 家族共性：达尔文的进化框架，孟德尔的遗传规律，摩尔根的基因变异，老愚公的移山精神。

GA，GP和GEP，乃至整个进化计算家族，闪耀着先贤和哲人的思想火花，有下列共性：达尔文的进化框架，孟德尔的遗传规律，摩尔根的基因变异，还有老愚公的移山精神。

算法思想和框架（粗可只看图，细则看解释）图3是遗传算法GA的进化流程，如果把其中编码方式换为GP的树，或GEP的基因表达式，就得到GP或GEP的流程。与上文（趣味数据挖掘系列9：灯谜、外星殖民、愚公移山和进化计算）的通例相比，图3稍细致一些：

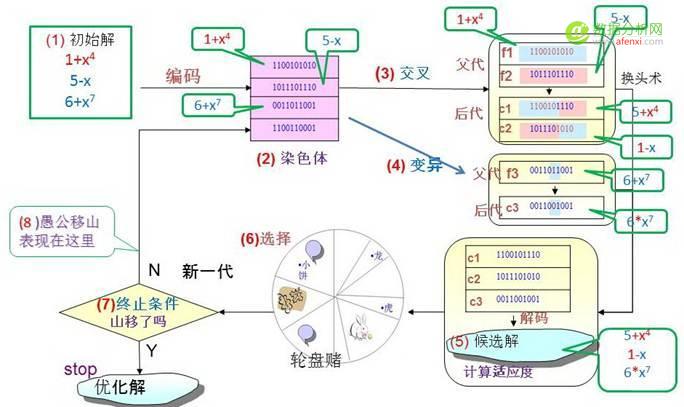
趣味数据挖掘系列10：基因表达式编程

图3 遗传算法的编码和进化流程示意图

图1的解释（初读时，不妨跳过）中给出了编码进化的流程，初始化的三个函数，与进化目标y=x+sin(x)的戴劳展式相差甚远，标注框中是编码前的公式，编码成为0与1的串。下面跟着红色的编号（1）-（6），略作说明：

(1)初始解，离谜底y=x+sin(x)较远；(2)三个公式编码成为01串联（图是示意性的）；(3)交叉，两个公式的编码实施换头术，得到后代C1和C2；(4)公式6+X ⁷ 变异成为6*x ⁷ (5) 编码解码成为公式，计算误差（适应度）

(6) 轮盘赌，可比喻为庙会上的“转糖饼”游戏，轮盘的转与停是随机过程，以此决定奖励品种，颇有点“费厄泼赖”，貌似公平；而庄家实则在扇区面积上做文章，成本低的品种被选中的机会越大（对应于进化计算中的术语：适应度越大），例如，图3中的轮盘赌来自“转糖饼”游戏，其中的“糖龙”与“糖虎” 成本高，对应的扇区小，指针停在这里的机会少；而小糖饼成本低，对应的扇区大，指针停在这里的机会多，小奖多而大奖少，从而维护了庄家的利益；

(7)检查终止条件，如果没有达到终止条件，进入下一代循环，这里表现了愚公移山故事中的“子子孙孙是没有穷尽的”。

5 简单编码解决复杂问题- 简单而奇妙的基因表达式编码

下图示意了GEP编码思路：图中有三个等价的表达：基因表达式，语法树和数学表达式：

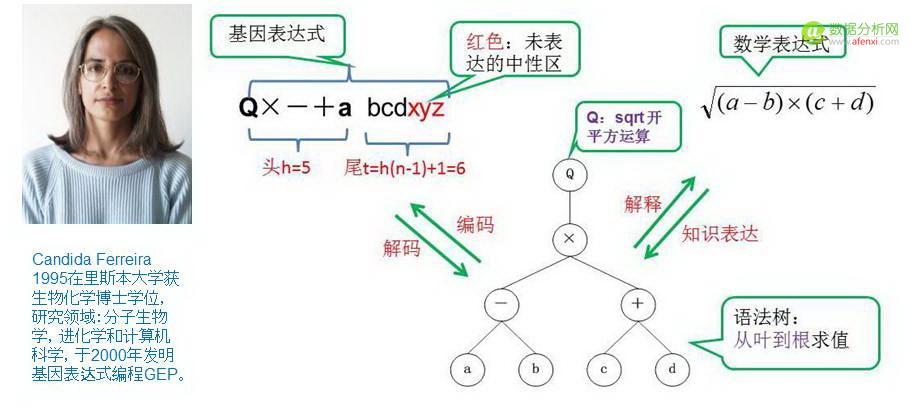
趣味数据挖掘系列10：基因表达式编程

图4 三个等价表达，基因表达式，语法树，数学表达式

知识解释：从语法树中，从叶到根归约

减号下面有，a和b, 归约得到a-b;

加号下面有，a和b, 归约得到a+b;

处理乘法符号，归约得到（a-b）* (c+d), （如程序语言中，*表示乘法）；

处理开平方符号Q，得到数学达式 ((a-b) * (c+d)) ^1/2

知识表达。按计算的优先级（如先乘除，后加减）展开，先算的在下,后算的在上，最后算的为根

编码过程语法树中，从上到下，从左到右，把符号写成一串（解码程序只需几十行）。

解码过程：从左到右，按指标生育，按次序表达，两个要点：

（a)节点按指标生育：开方只有一个参数，就只有子节点，+，-，*，/有两个参数，有两个子节点，If-Then-Else(或缩写为ITE）是一个运算的名称，有三个参数，即ITE节点有三个子节点。

(b)表达式中符号按次序表达。从基因表达式第一个符号开始表达：

首先表达Q（开方）：Q只需一个参数，建立以Q为根的树（此时，图中只有一个根节点Q）。

开平方运算Q需要一个被操作数（儿子），表达式中下一个符号是X（乘法），X被表达为Q的儿子。

乘法运算X 需要两个被操作数（儿子），表达式中下两个符号“-”和“+”，二者作X的儿子节点，于是“-”和“+”被表达；

减号- 需要两个被操作数，表达式中下两个符号是a和 b，二者作减号的儿子， a和 b已被表达为a-b；

加号+ 需要两个被操作数，表达式中下两个符号是c和 d，二者作加号的儿子， c和 d已被表达 c+d.

叶节点上全是常数，不再需要被操作对象了，表达完毕。

基因材料的供过于求与供不应求细心地读者会发现红色的xyz没有被表达，这种供过于求是好现象，模拟了生物基因中的中性区。如果供不应求，例如一个“+”号需要两个被操作数，基因表达中没有或只有一个被操作数，指向被操作数指针是空指针或者乱指针，将引起程序崩溃。

“平时看不见，偶尔露峥嵘”，中性区与隐性遗传，和生物基因中的中性区类似，中性区默默无闻地参加并积累着遗传和变异，但其对应的性状暂时没有表达出来。例如，图5中，x和y 是隐形基因，因为他们的父节点是常量a,而a不需要参数。假定有朝一日，符号a变异成为“+”，则“+”有两个生育指标，就把 x+y 表达出来了，原来结果中的这一个a会被（x+y）取代，最后结果变为((（x+y）-b)* (c+d)) ^1/2 ，如图5. 人群中的隔代遗传现象不知是否有类似解释,请专家指正。

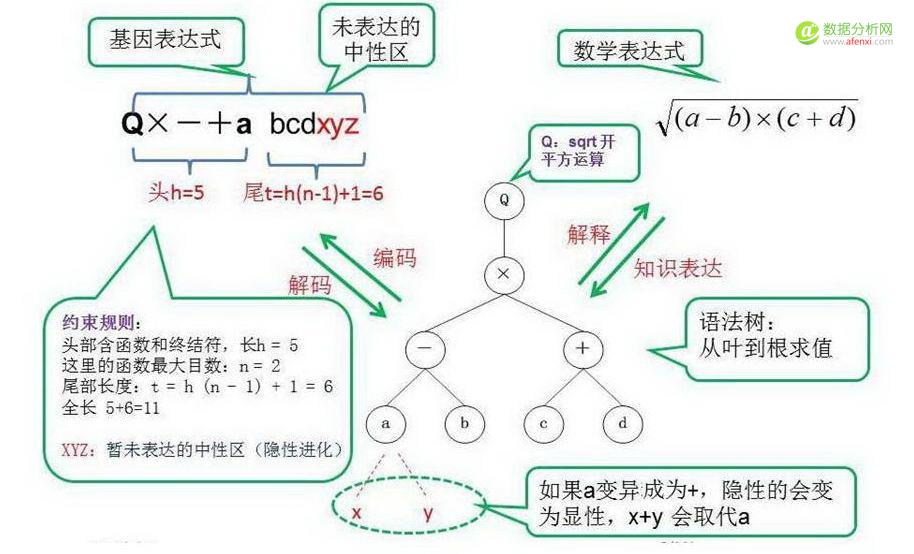
趣味数据挖掘系列10：基因表达式编程

图5 中性区“平时看不见，偶尔露峥嵘”

基因表达式编程的编码之妙：F.Cadidda 发明了基因表达式编程的编码方法，其最大的特点是：

（1）形串实树，藏复杂内容于平凡形式。参加遗传操作时,以线性串的平凡姿态，存储简单，处理快捷;解释语义时，用树的形式表达深刻的语义。

（2）生命力强，永不死亡，前面说过，在GA和GP中，染色体在残酷的遗传手术（如换头，挖心，加瘤）下大量死亡（有时，存活的不到1%），程序要花大量时间和空间去检查存活性，极大制约的进化的速度和质量，下面的定理将说明，基因表达式在遗传操作下永不死亡。

6 Candida的直觉和基因表达式基本定理获得了生物化学博士学位的Ferreira Candida有深厚生物医学背景,，在发明 GEP时候，她凭直觉采用了巧妙的形“串”实“树”的数据结构，给出了下列两个宽松的约束：

（a）内容约束：分成头尾两部分，头部可算符与参数；尾部不含算符，只有参数；

（b）长度约束：如果头长h,尾长t,计算符号最大目数（参数个数）为n，则须满足t=h(n-1)+1 。

Ferreira Candida直观感觉到，只要满足上述两条约束，头部的计算符号按生育指标索取子节点，在表达部分就有足够的被操作数供表达，不会出现供不应求的现象（而没有给证明或说明）。

供不应求对应于程序中使用未分配的指针或盲指针，例如，设P ₁ 和P ₂ 是指向参数的指针，做下列加法：

（*P ₁ ） + （*P ₂ ），其中P ₁ ，P ₂ 是未分配的指针或盲指针，则可能引起程序崩溃或计算错误。

2002年，我们的研究团队用数学归纳法严格地证明了：只要染色体满足上述两个（宽松的）约束, 则在任意残酷基因手术下，染色体永不死亡（参见文献[5]）。

这个定理有时被称为GEP基本定理，它给出了GEP可行可信的理论依据。

科学家和工程师的好工具。对于实验科学家和工程师，如果想自己开发一套GEP挖掘系统，需要半年或一年以上的学习（时间依赖于相关基础）；如果使用现成的商品化的GEP系统，只需要几周的学习；这有点像造一个程序语言和使用程序语言的差别。程序语言即便简单如BASIC，也需要一定时间的学习，学好用好一个较复杂的语言(如C）要一年以上的学习和实践。

在网上搜索Ferreira Candida 或GEP ，可以得到更多的信息，可以查到他们的公司和软件产品。也容易查到国内外研究者的成果和进展。

使用现成的系统，经过不太长时间的学习，可从自己的实验数据中挖掘经验公式、类似于发现类似于太阳黑子规律、类似与开普勒定律的数学方程、设计门电路，还可以挖掘关联规则、分类规则、聚类规则、逻辑规则，等等。

下篇博文，拟讨论数据挖掘的十大算法以及十大问题。