贝叶斯深度学习——基于PyMC3的变分推理

目前机器学习的发展趋势

目前机器学习有三大趋势： 概率编程 、 深度学习 和“ 大数据 ”。在概率编程（PP）方面，有许多创新，它们大规模使用 变分推理 。在这篇博客中，我将展示如何使用 PyMC3 中的变分推理来拟合一个简单的贝叶斯神经网络。我还将讨论桥接概率编程与深度学习能够为将来研究开创怎样的有趣途径。

大规模概率编程

概率编程可以灵活创建自定义概率模型，主要关注从数据中洞悉和学习。这种方法本质上是贝叶斯方法，所以我们可以指定先验来告知和约束我们的模型，并得到后验分布形式的不确定性估计。使用MCMC采样算法，我们可以从后验中抽样灵活地估计这些模型。 PyMC3 和Stan是目前用来构建并估计这些模型最先进的工具。但是，采样的一个主要缺点就是它往往非常耗时，特别是对于高维度模型。这就是为什么最近变分推理算法得到发展，它几乎与MCMC同样灵活，但是更快。这些算法拟合后验的分布（比如正态分布），将采样问题转换为优化问题，而不是从后验中采样。 ADVI ——自动微分变分推理（Automatic Differentation Variational Inference）——在PyMC3和 Stan 中已经实现，一个新的包 Edward 同样得到了实现，它主要与变分推理有关。

不幸的是，当面临传统的机器学习问题时，比如分类或（非线性）回归，与集成学习（比如随机森林或梯度提升回归树）这样的算法相比，概率编程不能胜任（精度和可扩展性方面）。

深度学习

现在深度学习第三次复兴，它已经成为头条新闻，支配了几乎所有的物体识别基准，在Atari游戏中获胜，并且战胜了世界围棋冠军李世石。从统计学角度看，神经网络非常擅长非线性函数逼近和表示法学习。大多数为人所知的是分类任务，它们已经通过AutoEncoders和其他各种有趣的方法（比如循环网络，或使用MDN来估计多模态分布）扩展到了非监督学习。它们的效果为何如此好？没有人真正知道原因，因为这些统计特性仍不为人完全理解。

深度学习很大一部分创新是可以训练极其复杂的模型。这依赖于几个支柱：

• 速度：提高GPU性能获得更快的处理。
• 软件：像 Theano 和 TensorFlow 这样的框架允许灵活创建抽象模型，然后可以对其优化并编译到CPU或GPU上。
• 学习算法：在数据子集上训练——随机梯度下降——可以让我们在海量数据上训练这些模型。使用drop-out这样的技术可以避免过拟合。
• 架构：大量的创新都是改变输入层，比如卷积神经网络，或改变输出层，比如 MDN 。

桥接深度学习和概率编程

一方面，概率编程可以让我们以原则化和易于理解的方式构建比较小的，集中的模型来深入了解数据；在另一方面，使用深度学习的启发式方法来训练大量和高度复杂的模型，这些模型的预测效果惊人。最近变分推理中的创新能够使概率编程扩大模型的复杂性和数据大小。所以，我们处于结合这两种方法的风口浪尖，希望能在机器学习方面解锁新的创新。想了解更多，也可以看看 Dustin Tran 最近的 博客文章 。

这种桥接可以让概率编程被运用于一系列更广泛的有趣问题中，我相信它同样能在深度学习方面有所创新。比如：

• 预测中的不确定性 ：我们下面将会看到，贝叶斯神经网络告诉我们它的预测中的不确定性。我认为不确定性是机器学习中被低估的概念，因为它对现实世界的应用来说显然是重要的。它在训练中也非常有用。比如，我们可以在模型最不确定的样本中来训练模型。
• 表示中的不确定性 ：我们同样会得到权重的不确定估计，它可以告诉我们网络中学习到的表示的稳定性。
• 先验正则 ：权重往往通过L2正则化来避免过拟合，这很自然地在权重系数上使用高斯先验。我们可以想象其他各种先验，比如spike-and-slab 来加强稀疏程度（使用L1范数更合适）。
• 知情先验的迁移学习 ：如果我们想在一个新的物体识别数据集上训练网络，我们可以使用其他预训练的网络生成的权值作为知情先验来引导学习，比如 GoogLeNet 。
• 分层神经网络 ：概率编程中一种强大的方法是分层建模，可以将在子组中学习到的东西池化运用于全局（见 PyMC3分层线性回归 教程）。在分层数据集中运用神经网络，我们可以对子组训练单个神经网络，而同时还能获得全局的表示。比如，假设一个网络被训练用来从汽车图片中分类车型。我们可以训练一个分层神经网络，其中一个子网络仅用来分辨某个制造商生产的车型。直觉告诉我们，某个制造商的所有车辆都有相似之处，所以针对特定品牌来训练单个网络完全说的通。然而，由于各个单个网络都与上一层相连，它们仍然可以与其他特定的子网络共享特征信息，这些特征对于所有品牌都有用。有趣的是，网络的不同层可以从分层不同的级别中获得信息——例如，提取视觉线条的初层在所有子网络中都是同一的，而高阶表示则不同。分层模型可以从数据中学习到所有东西。
• 其他混合架构 ：我们可以自由地构建各种神经网络。例如，贝叶斯非参数化可以用来灵活调整隐藏层的大小和形状，根据在训练过程中碰到的问题最佳地扩展网络架构。目前，这需要昂贵的超参数优化和大量的系统知识。

PyMC3中的贝叶斯神经网络

生成数据

首先，我们生成一些小型数据——一个简单的二元分类问题，非线性可分。

In [1]:

%matplotlib inline import pymc3 as pm import theano.tensor as T import theano import sklearn import numpy as np import matplotlib.pyplot as plt import seaborn as sns sns.set_style('white') from sklearn import datasets from sklearn.preprocessing import scale from sklearn.cross_validation import train_test_split from sklearn.datasets import make_moons

In [2]:

X, Y = make_moons(noise=0.2, random_state=0, n_samples=1000) X = scale(X) X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=.5)

In [3]:

fig, ax = plt.subplots() ax.scatter(X[Y==0, 0], X[Y==0, 1], label='Class 0') ax.scatter(X[Y==1, 0], X[Y==1, 1], color='r', label='Class 1') sns.despine(); ax.legend() ax.set(xlabel='X', ylabel='Y', title='Toy binary classification data set');

模型规格

神经网络很简单。最基本的单元是一个感知器，它只不过是一个逻辑回归实现。我们并行使用许多这样的单元，然后堆叠起来组成隐藏层。在这里，我们将使用2个隐藏层，每层5个神经元，处理这个简单的问题足够了。

In [17]:

# Trick: Turn inputs and outputs into shared variables.  # It's still the same thing, but we can later change the values of the shared variable  # (to switch in the test-data later) and pymc3 will just use the new data.  # Kind-of like a pointer we can redirect. # For more info, see: http://deeplearning.net/software/theano/library/compile/shared.html ann_input = theano.shared(X_train) ann_output = theano.shared(Y_train)  n_hidden = 5  # Initialize random weights between each layer init_1 = np.random.randn(X.shape[1], n_hidden) init_2 = np.random.randn(n_hidden, n_hidden) init_out = np.random.randn(n_hidden)  with pm.Model() as neural_network:     # Weights from input to hidden layer     weights_in_1 = pm.Normal('w_in_1', 0, sd=1,                               shape=(X.shape[1], n_hidden),                               testval=init_1)      # Weights from 1st to 2nd layer     weights_1_2 = pm.Normal('w_1_2', 0, sd=1,                              shape=(n_hidden, n_hidden),                              testval=init_2)      # Weights from hidden layer to output     weights_2_out = pm.Normal('w_2_out', 0, sd=1,                                shape=(n_hidden,),                                testval=init_out)      # Build neural-network using tanh activation function     act_1 = T.tanh(T.dot(ann_input,                           weights_in_1))     act_2 = T.tanh(T.dot(act_1,                           weights_1_2))     act_out = T.nnet.sigmoid(T.dot(act_2,                                     weights_2_out))      # Binary classification -> Bernoulli likelihood     out = pm.Bernoulli('out',                         act_out,                        observed=ann_output)

还不错。Normal先验用来正则化权值。通常我们会在输入中加入一个常数b，但为代码简洁起见，我在这里省略了。

变分推理：扩展模型复杂性

现在我们已经可以运行一个MCMC采样器了，比如NUTS，在这里效果非常不错，但是正如我前面提到的，当我们扩展模型到更深的架构，更多层时，处理起来会非常缓慢。

不过我们将使用最近加入到PyMC3全新的ADVI变分推理算法。这种算法更快而且能够更好地扩展。注意，这是平均场近似，所以我们忽略后验相关性。

In [34]:

%%time with neural_network:     # Run ADVI which returns posterior means, standard deviations, and the evidence lower bound (ELBO)     v_params = pm.variational.advi(n=50000)  Iteration 0 [0%]: ELBO = -368.86 Iteration 5000 [10%]: ELBO = -185.65 Iteration 10000 [20%]: ELBO = -197.23 Iteration 15000 [30%]: ELBO = -203.2 Iteration 20000 [40%]: ELBO = -192.46 Iteration 25000 [50%]: ELBO = -198.8 Iteration 30000 [60%]: ELBO = -183.39 Iteration 35000 [70%]: ELBO = -185.04 Iteration 40000 [80%]: ELBO = -187.56 Iteration 45000 [90%]: ELBO = -192.32 Finished [100%]: ELBO = -225.56 CPU times: user 36.3 s, sys: 60 ms, total: 36.4 s Wall time: 37.2 s

在我老旧的笔记本上耗时小于40秒。这相当不错，考虑到NUTS将会花费相当多的时间。在下面，我们又会减少运行时间。想让它有质的飞跃，我们可能要在GPU上训练神经网络。

由于这些样本非常便于处理，我们可以使用sample_vp()（这只是从正态分布中取样，所以与MCMC完全不同）从变分后验中很快地提取样本：

In [35]:

with neural_network:     trace = pm.variational.sample_vp(v_params, draws=5000)

绘制目标函数（ELBO），我们可以看出随着时间推移，拟合效果越来越好。

In [36]:

plt.plot(v_params.elbo_vals) plt.ylabel('ELBO') plt.xlabel('iteration')

Out[36]:

<matplotlib.text.Text at 0x7fa5dae039b0>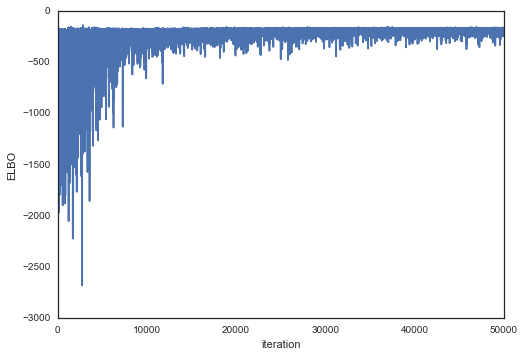

现在我们已经训练了模型，接下来我们使用后验预测检查（PPC）在测试集上进行预测。我们使用sample_ppc()从后验（从变分估计中采样）中生成新的数据（在此例中是类别预测）。

In [7]:

# Replace shared variables with testing set ann_input.set_value(X_test) ann_output.set_value(Y_test)  # Creater posterior predictive samples ppc = pm.sample_ppc(trace, model=neural_network, samples=500)  # Use probability of > 0.5 to assume prediction of class 1 pred = ppc['out'].mean(axis=0) > 0.5 

In [8]:

fig, ax = plt.subplots() ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1]) ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r') sns.despine() ax.set(title='Predicted labels in testing set', xlabel='X', ylabel='Y');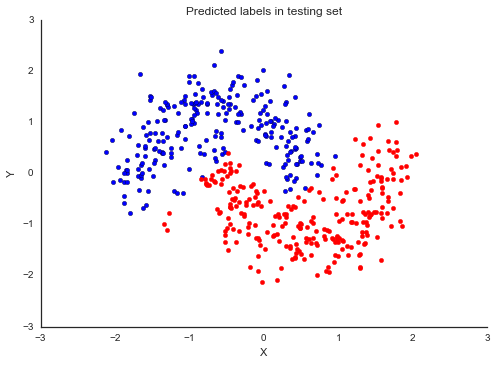

In [9]:

print('Accuracy = {}%'.format((Y_test == pred).mean() * 100))

嘿，我们训练的神经网络效果非常好！

来看看分类器学到了什么

在这里，我们在所有输入空间里评估类别概率预测。

In [10]:

grid = np.mgrid[-3:3:100j,-3:3:100j] grid_2d = grid.reshape(2, -1).T dummy_out = np.ones(grid.shape[1], dtype=np.int8)

In [11]:

ann_input.set_value(grid_2d) ann_output.set_value(dummy_out)  # Creater posterior predictive samples ppc = pm.sample_ppc(trace, model=neural_network, samples=500)

概率面

In [26]:

cmap = sns.diverging_palette(250, 12, s=85, l=25, as_cmap=True) fig, ax = plt.subplots(figsize=(10, 6)) contour = ax.contourf(*grid, ppc['out'].mean(axis=0).reshape(100, 100), cmap=cmap) ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1]) ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r') cbar = plt.colorbar(contour, ax=ax) _ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel='X', ylabel='Y'); cbar.ax.set_ylabel('Posterior predictive mean probability of class label = 0');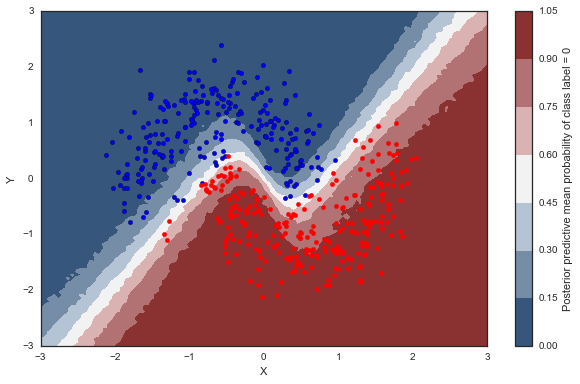

预测值中的不确定性

目前为止，我向大家展示的所有事情都能用非贝叶斯神经网络完成。对于每个类别的后验预测的平均值应该与最大似然预测值相同。然而，我们也可以看看后验预测的标准差来了解预测中的不确定性。就是下面这样子：

In [27]:

cmap = sns.cubehelix_palette(light=1, as_cmap=True) fig, ax = plt.subplots(figsize=(10, 6)) contour = ax.contourf(*grid, ppc['out'].std(axis=0).reshape(100, 100), cmap=cmap) ax.scatter(X_test[pred==0, 0], X_test[pred==0, 1]) ax.scatter(X_test[pred==1, 0], X_test[pred==1, 1], color='r') cbar = plt.colorbar(contour, ax=ax) _ = ax.set(xlim=(-3, 3), ylim=(-3, 3), xlabel='X', ylabel='Y'); cbar.ax.set_ylabel('Uncertainty (posterior predictive standard deviation)');

小批次ADVI：扩展数据大小

目前，我们在所有数据上训练了模型。显然，这不能扩展到ImageNet这样的数据集上。此外，在小批次数据（随机梯度下降）上训练可以避免局部最小，并可能加快收敛。

幸运的是，ADVI可以在小批次数据上运行。它只需要进行一些设置：

In [43]:

# Set back to original data to retrain ann_input.set_value(X_train) ann_output.set_value(Y_train)  # Tensors and RV that will be using mini-batches minibatch_tensors = [ann_input, ann_output] minibatch_RVs = [out]  # Generator that returns mini-batches in each iteration def create_minibatch(data):     rng = np.random.RandomState(0)      while True:         # Return random data samples of set size 100 each iteration         ixs = rng.randint(len(data), size=50)         yield data[ixs]  minibatches = [     create_minibatch(X_train),      create_minibatch(Y_train), ]  total_size = len(Y_train)

上面的代码看起来有点吓人，但我很喜欢这种设计。特别是你定义了一个非常灵活的生成器。原则上，我们可以从数据库中获取数据，而且不需要将所有数据放在RAM中。

我们把它们传给advi_minibatch()：

In [48]:

%%time with neural_network:     # Run advi_minibatch     v_params = pm.variational.advi_minibatch(         n=50000, minibatch_tensors=minibatch_tensors,          minibatch_RVs=minibatch_RVs, minibatches=minibatches,          total_size=total_size, learning_rate=1e-2, epsilon=1.0     )

In [49]:

with neural_network:         trace = pm.variational.sample_vp(v_params, draws=5000)

In [50]:

plt.plot(v_params.elbo_vals) plt.ylabel('ELBO') plt.xlabel('iteration') sns.despine()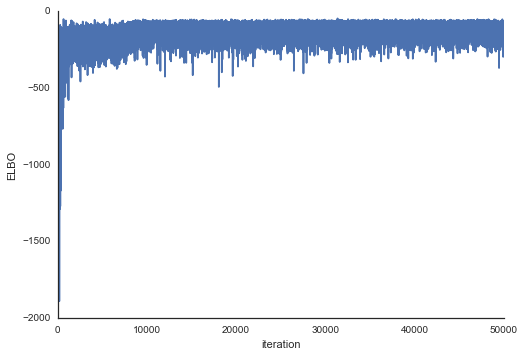

正如你所看到的，小批次ADVI的运行时间要少的多。它似乎也收敛的更快。

为了好玩，我们也可以看看轨迹。我们在神经网络权值中同样会有不确定性。

In [51]:

pm.traceplot(trace);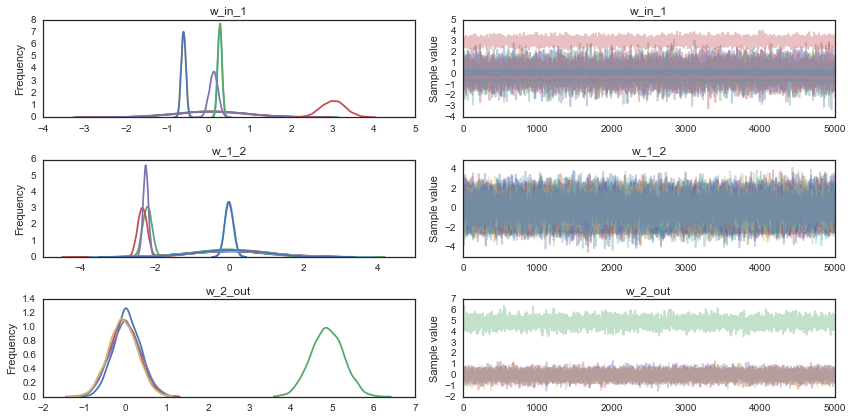

总结

希望这篇博客很好地讲述了PyMC3中一种强大的新型推理算法：ADVI。我同样认为桥接概率编程和深度学习能够为此领域开辟许多新渠道的创新，上面已经讨论。特别地，分层神经网络听起来相当牛逼。这真是激动人心的时刻。

下一步

使用PyMC3作为计算后端的Theano，主要用于估计神经网络，而且有许多类似于Lasagne的非常棒的库，来使简化最常见的神经网络架构的构建，这些库构建于Theano之上。理想情况下，我们不需要像上面那样手动构建模型，而是使用Lasagne方便的语法来构建网络体系结构，定义先验，并运行ADVI。虽然我们还没有成功地在GPU上运行PyMC3，但是这应该没什么难度（因为Theano能够在GPU上运行），并且能够进一步大幅减少运行时间。如果你了解Theano，这将会是你发挥作用的领域！

你可能会说，上面的网络不是很深，但请注意，我们可以很容易地扩展到更多层，包括卷积层，用来在更具挑战的数据集上进行训练。

我也提供了一些我在PyData London的一些工作资料，见下面的视频：

https://www.youtube.com/embed/LlzVlqVzeD8

最后，你可以在 这里 下载NB。在下面的评论区留言，并关注 我的Twitter 。

致谢

Taku Yoshioka 为PyMC3的ADVI做了很多工作，包括小批次实现和从变分后验采样。我同样要感谢Stan的开发者（特别是Alp Kucukelbir和Daniel Lee）派生ADVI并且指导我们。感谢Chris Fonnesbeck、Andrew Campbell、Taku Yoshioka和Peadar Coyle为早期版本提供有用的意见。