重磅 | MIT与谷歌专家合著论文：机器学习和神经科学的相互启发与融合（附论文）

摘 要

神经科学专注的点包括计算的细节实现，还有对神经编码、力学以及回路的研究。然而，在机器学习领域，人工神经网络则倾向于避免出现这些，而是往往使用简单和相对统一的初始结构，以支持成本函数（cost funcion）的蛮力最优化。近期出现了两项机器学习方面的进展，或许会将这两种看似不同的视角连接起来。第一，结构化的架构得以使用，这些架构包括注意力、递归，以及各种长、短期记忆储存专用系统。第二，随着时间以及层数的变化，成本函数和训练程序也会变化并越来越复杂。我们根据这些理论，对大脑进行了进一步思考，并作出如下假设：（1）大脑最优化成本函数，（2）在大脑成长的不同时期，或在大脑中的不同位置中，成本函数各不相同，种类多样。（3）预构建的架构与行为引发的计算问题相匹配，优化就在这种架构中进行。这样一个由一系列互相影响的成本函数支撑的混杂的优化系统，旨在让学习更加有效地应用数据，更精确地瞄准机制的需要。我们建议了一些方向，神经科学研究人员可以对这些假设进行改进和测试。

引 言

当今的机器学习和神经科学领域没有共同话题。脑科学领域中，已经发现了一系列不同的大脑区域、细胞类型、分子、元胞状态、计算和信息存储机制等。相比之下，机器学习则主要关注单个原则的实例化：函数优化。据研究发现，最小化分类错误等简单的目标优化，就可能会使多个网络层和循环网络中形成大量的内在表征和强大的算法能力。（LeCun et al.，2015；Schmidhuber，2015）。下面我们看看如何将这些观点统一起来。

当然，机器学习中占主导地位的人工神经网络最初来源于神经科学的启发（McCulloch and Pitts，1943）。虽然神经科学一直在发挥作用（Cox and Dean，2014），但其中很多重大突破，都不是得益于神经科学的发现（Sutskever and Martens， 2013），而是因为人们对有效优化问题中的数学问题进行洞察而受到了启发。该领域从简单的线性系统（Minsky and Papert， 1972），发展为非线性网络（Haykin，1994），然后成为深度和循环网络（Schmidhuber，2015； LeCun et al.， 2015）。

误差的反向传播（Werbos， 1974， 1982；Rumelhart et al.， 1986）提供了一种有效的方法，可以计算与多层网络权重相关的梯度，使得神经网络可以进行有效的训练。训练的方法不断提升，开始包含冲量项，更优良的权重初始化，共轭梯度等，经过这样的演化，形成了现在用批量随机梯度下降实现优化的网络。这些进展与神经科学几乎没有明显的关联。

然而，我们认为神经科学和机器学习已经准备好再次汇聚。论文中关于机器学习有三个重要方面：

第一，机器学习主要关注成本函数的最优化问题（见下图）。

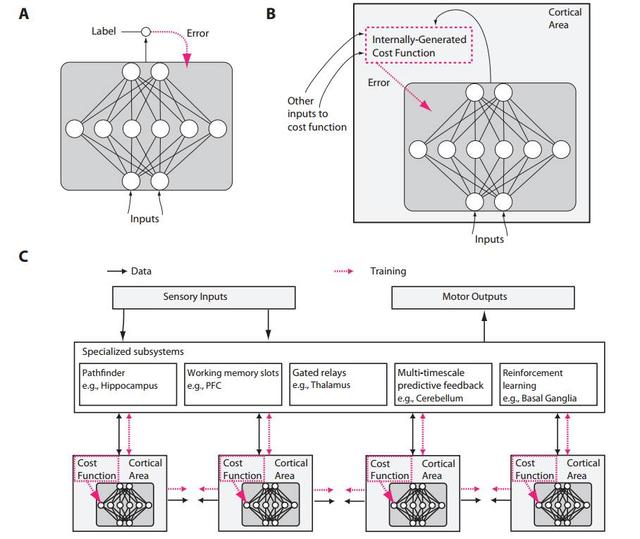
图1：传统设计和类脑神经网络设计之间假定的区别。A）在传统深度学习中，监督训练是基于外部提供的标记数据。B）在大脑中，网络的监督训练能通过在错误信号上的梯度下降静态发生，但这一 错误信号必须是由内部生成的成本函数产生。这些成本函数通过神经模块进行自计算，而神经模块是由遗传和学习特定的。内部生成的成本函数创造启发能力，能够自助产生更复杂的学习能力。例如，一个识别面部的大脑区域可能首先会被训练使用简单启发能力检测面部，就像一条线上面有两个点，然后使用由非监督学习和错误信号（从其他与社会奖励流程有关的脑部区域产生的信号）产生的表征进一步训练如何区别有特色的面部表情。C）内部生成的成本函数和皮质深度网络的错误驱动训练部分组成了一个更大的包含数个专门系统的架构。尽管可训练的皮质区域在这里扼要表示为前馈神经网络，LSTM 或其他类型的循环网络可能会是一个更为精准的类比。而且，树突计算、spiking 神经网络、神经调节、自适应、 TDP（timing-dependent plasticity）等很多的神经特性将影响到网络如何学习、学习什么。

第二，最近的机器学习研究中，已经开始引入复杂的成本函数，这些函数在不同网络层中和不同时间下并不统一，而且它们形成于网络不同部分的交互中。比如，为低层次网络引入时间相干性（随空间变化的非统一成本函数）的目标会提升特征学习的性能（Sermanet and Kavukcuoglu，2013）。还有一个源于内部交互的成本函数的例子，即成本函数时间表（随时间变化的非统一成本函数） 会提升泛化能力（Saxe et al.， 2013；Goodfellow et al.， 2014b； G¨ul，cehre and Bengio，2016）和对抗网络的性能， 这使得生成模型可以基于梯度进行训练（Goodfellow et al.， 2014a）。易于训练的网络可以用来提供「hint」（提示），以帮助更强大的网络进行自助训练。（Romero et al. ，2014）

第三，机器学习中，受最优化约束的架构已经开始变得多样化。如今，机器学习已经引入的内容包括：简单记忆细胞，这些细胞持有多个连续状态（Hochreiter and Schmidhuber， 1997；Chung et al.， 2014）；含有「capsules」（胶囊）等架构的更复杂的基本单元（Hinton et al.， 2011； Livni et al.，2013；Delalleau and Bengio，2011；Tang et al.，2012）；以及内容可寻址存储器和位置可寻址存储器（Graves et al.， 2014）；指针（Kurach et al.， 2015）；硬编码算术操作（Neelakantan et al.，2015）等。目前，我们的这三条假设还未引起神经科学界的广泛关注，因此我们将其阐述了出来，并对其进行考究，然后描述了实验和测试的方法。首先，让我们再对其进行更准确的陈述。

假设1——大脑最优化成本函数

连接这两个领域的核心假设是生物系统能像其他很多机器学习系统一样能够优化成本函数。成本函数的思路意味着大脑中的神经元如何改变它们的特性，例如，神经突触的特性，如此无论成本函数怎么定义它们的角色，它们都能变得更好。人类行为有时在某个领域会有最优方法，例如运动行为中（K¨ording, 2007），这表明大脑可能学习到了最优策略。对象在移动系统中，会最低限度的消耗能量（Taylor and Faisal, 2011），并且会采取风险最低、对身体损伤最小的方式，同时，最大化金钱和活动上的收获。从计算上来看，我们现在知道移动轨迹的最优化为每一个复杂的运动任务提供了精致的解决方案（Mordatch et al., 2012; Todorov and Jordan, 2002; Harris and Wolpert, 1998）。我们提议，在大脑使用的内部表征和流程的塑造上有更为普遍的成本函数最优化。我们同样表明，这需要大脑在多层网络和循环网络中有着有效的信用分配机制。

假设2——成本函数因区域不同而有区别，也会随着发育而改变

第二个实现原则是成本函数不需要是全局的。不同大脑区域的神经元可能优化不同的事情，比如，运动行为的均方差，在视觉刺激或注意力分配行为中可能变得令人惊奇。重要的是，这样的一个成本函数能够在本地生成。例如，神经元能够本地评估输入的统计模型的质量（图 1B ）。作为一种替代选择，某一领域的成本函数可由另一领域生成。另外，成本函数可能会随时间发生变化，比如，早些时候引导年轻人理解简单的视觉对比，晚些时候再做一次。这可能会让成长中的大脑基于简单的知识自助产生更为复杂的知识。大脑中的成本函数可能因不同的区域有不同的复杂度，也会随大脑发育而产生变化。

假设 3——专业化系统能够高效解决关键计算问题

第三个实现原则是结构很重要。看起来，大脑不同区域的信息流模式不同，这表明它们解决不同的计算问题。一些大脑区域高度循环，这注定它们进行短期记忆存储 （Wang, 2012）。一些区域包含的细胞能够在不同的活化状态间切换，比如，作为对特定神经递质的回应，一个持续释放信号的模式与一个瞬时释放信号的模式。其他区域的信息流过丘脑时，丘脑似乎能掌握这些信息。像是丘脑这样的其他区域可能会让它们决定信息的路线（Sherman, 2005）。像基底神经节（basal ganglia）这样的区域涉及到强化学习和离散决策的门脉（Sejnowski and Poizner, 2014; Doya, 1999），就像每一个程序员了解的那样，专门算法对计算问题有效的解决方案很重要，而大脑似乎很善于利用这样的专门化（图 1C）。

这些思路受到了机器学习近期进展的启发，但我们也提出了大脑与如今的机器学习技术有很大区别。特别是，我们能够用于监督学习的信息量是有限的（Fodor and Crowther, 2002）。虽然可用于无监督学习的信息量非常大，但无论其多么强大，我们毫无理由假设出一个通用的无监督算法，为了掌握这些知识能够学习人类需要知道的精确事务。因此，进行无监督学习的发展挑战是解决「正确的」问题，去发现一系列的成本函数。这些成本函数将根据描述的发展阶段，确切地建立回路和行为，以便于最终用相当小的一部分信息就足以产生正确行为。例如，一个成长中的鸭子会铭记其父母的模板（Tinbergen, 1965），然后使用这一模板产生帮助其发展其他技能的目标靶向，比如觅食能力。

从此研究和其他研究（Ullman et al., 2012; Minsky, 1977）中进行归纳，我们提出，很多的大脑成本函数产生于这样的一个内部自助过程（internal bootstrapping process）。确实，我们提出生物发育和强化学习实质上能够编写出一系列成本函数，这些成本函数可精确的预料大脑内部子系统和整个机制需要的面对的未来状况。这类的发育型编写自助法会产生成本函数的一个内部基础架构，既不同又复杂，然而这可以简化大脑内部流程面临的学习问题。超越家族印记这样的简单任务，这类自助法可扩展出高度的认知能力，例如，内部生成的成本函数可训练一个发育中的大脑，让其适当的获取记忆，或以一种有用的方式组织自我行为。我们将考虑在无监督和强化学习环境中运用这种潜在的自助机制，超越如今机器学习中使用的这种课程式学习思路（Bengio et al., 2009）。

在此论文的其他部分，我们将详细说明这些假设。首先，我们认为局部和多层最优化是与我们所知的大脑兼容的，这可能会令人惊讶。第二点，我们认为成本函数因大脑区域不同而不同，也会随时间发生变化，并且将会描述成本函数如何以一种协调的方式相互作用从而准许复杂函数的自展。第三，我们将列出一组广泛的、需要由神经计算解决的专门问题。而后，我们讨论了上述假设对神经科学和机器学习研究途径的一些影响，而且梗概描述了一组实验测试这些假设。最终，我们从进化的角度讨论了这一体系结构。

机器学习启发下的神经科学

如果一个假设能够带来合乎实际且可测试的预测，它就是有用的。所以，现在我们希望重新回顾一下这些神经科学上的假设，看看可以在那个层面上直接测试这些测试，以及通过神经科学加以改善。

假设1 —— 成本函数的存在

有很多一般策略（general strategies）来解决这个问题：大脑是否以及如何优化成本函数。第一个策略是以观察学习终结点（endpoint）为基础的。如果大脑使用了一个成本函数，而且我们能够猜出它的身份（identity），大脑的最终态应该接近成本函数最优（optimal for the cost function ）。如果知道自然环境的统计情况，并且知道这个成本函数，那么，我们就能比较在仿真中得以优化的接受域（receptive fields）和被测量的接受域。人们刚刚开始使用这一策略，因为很难测量接受域或大量神经元的其他表征特征，但随着大规模记录方法的出现，这种情况正在从技术上开始被改善。

第二种方法可以直接量化成本函数描述学习的优良度。如果学习的动态性最小化了一个成本函数，那么，基础的向量场应该有一个强梯度下降法类型组件和一个弱转动组件（weak rotational component）。如果我们能在某种程度上，持续监测突触强度，并从外部操纵它们，那么，原则上，我们就可以在突触权重空间中测量向量场，并计算其散度和旋转。对于至少一组正在通过某种逼近梯度下降方式接受训练的突触子集来说，较之转动组件，发散组件应当强壮一些。由于需要监测大量突触权重，实验难度阻碍了这一策略的发展。

第三种方法的基础是摄动函数：基于学习的成本函数应该可以撤销打断最优的摄动带来的影响。举个例子，在摄动之后，系统应该回到最小值，而且实际上，在一次足够小的摄动后，或许回到同一个本地最小值。如果我们改变突触联系，比如，在脑机界面的语境中，我们应该能够得到一个重组，可以根据猜出的相关成本函数预测到它。在大脑皮层的运动区，这一策略正在变得可行。

最后，如果我们从结构上知道，哪些细胞类型和连接调节着错误信号vs输入数据或其他类型连接，那么，就可以刺激特定连接，以便施加一个用户界定的成本函数。实际上，我们可以使用大脑自己的网络作为一个可训练的深度学习底层（substrate），然后研究网络如何响应训练。脑机界面可被用来设置特定的本地学习问题，其中，要求大脑创建某些用户指定的表征，而且，这一过程的动态性可以受到监控(Sadtler et al .,2014)。为了合理做到这一点，首先，更多地了解被连接用于传输成本信号的系统。比如，可以在连接组回路图中找到的结构中的大部分内容，不仅仅与短时间计算相关，也是为了创造出支持成本函数及其优化的基础架构。

文中已经讨论过的许多学习机制都对连接性或动态进行了具体预测。比如，生物BP的「反馈校准（feedback alignment） 」表明，在神经元分组（neuronal grouping）水平上，皮层反馈连接应当在很大程度上与相应的反馈连接协调起来。

一些为了学习时间序列，吸收了树突巧合监测（dendritic coincidence detection）的模型，预测出一个给定的轴突在给定的树突段只能产生少量突出（Hawkins and Ahmad, 2015）。涉及 STDP 的学习模型将预测改变放电率的动态情况(Hinton, 2007, 2016; Bengio et al., 2015a; Bengio and Fischer, 2015; Bengio et al., 2015b)，也会预测特定的网络结构，例如，那些基于自编码器或者再循环的网络结构。其中，STDP 可以产生一种反向传播的形式。

关键在于建立起优化的单元。我们想知道，可以通过某种梯度下降最优相似法加以训练的模块规模。共享一个给定误差信号或成本函数的网络的大小如何？在何等规模上，适当的训练信号可以被传递？可以说，原则上，大脑被端对端优化了。在这种情况下，我们会期待找到将训练信号从每层传到前一层的连接。

优化可以以连续较小规模的方式发生在一个大脑区域里，比如，一个微回路或者一神经元(K¨ording and K¨onig, 2000, 2001; Mel, 1992; Hawkins and Ahmad, 2015) 。重要的是，这些优化可以在这些规模上共存。可能会有一些端到端的慢性优化，也可能在某个局部区域有更强大的优化方法，以及每个细胞内部可能有非常有效的算法。精心设计的实验可以识别出优化规模，比如，通过区域摄动来量化学习范围。

在某种程度上，结构函数的紧密关系是分子和细胞生物学的标志，但是，在大型链结式学习系统中，这种关系却难以提取：通过让其经受不同训练，可以驱动相同的初始网络去计算很多不同的函数。但是，理解神经网络解决问题的方式，还是很难的。

怎么样才能分辨出梯度下降训练网络、未经训练或随机的网络、被训练用来针对某一种特定任务的网络之间的区别呢？一种可能的方法是训练人工神经网络来对抗各类候选成本函数，研究产生的神经调谐特性(Todorov, 2002)，然后将它们与那些兴趣电路进行比较 (Zipser and Andersen, 1988)。这种方法已经在 PFC 解释神经动力学基础决策中有所应用(Sussillo, 2014)，并且在后顶叶皮层记忆，后顶叶皮层的工作记忆，以及视觉系统的物体呈现中发挥作用(Rajan et al., 2016)。在任何情况下，复杂机器学习系统逆向工程的有效分析方法 和生物大脑逆向工程的方法可能有一些共性。

这是否强调了功能优化和可训练基板意味着我们应该放弃基于细节测量和特定的相关性与动态模式大脑逆向工程？

相反：我们应该大规模绘制脑谱，试着更好地理解 a）大脑如何实现优化，b）训练信号从哪里来和它们体现了什么成本函数，还有 c）在不同的组织水平上，存在什么样的结构来约束这个优化以有效找到这类特定问题的解决方法。答案也许会受到神经元和网络本身不同性质的影响，如神经结构的同质化规则，基因表达和功能 ，突触类型的多样性和细胞类型的特定连接 （Jiang et al., 2015），层间的模式预测和抑制神经元类型的分布，和树突状目标以及树突状定位和本地树突的生理性和可塑性（ Markram et al., 2015; Bloss et al., 2016; Sandler et al., 2016），或者局部神经胶质网。它们也可能受到更高级别的大脑神经系统的综合性质，包括发展引导机制（Ullman et al., 2012），信息由路 （Gurney et al., 2001; Stocco et al., 2010），以及注意力（Buschman and Miller, 2010）和分层决策的影响 (Lee et al., 2015)。

绘制这些系统的细节对于理解大脑如何工作至关重要，下至至纳米级的离子通道树突状组织，上至皮质、纹状体（striatum）和海马体的全局协调，所有这些在我们详细说明的框架中都计算性相关。因此我们预计大规模、 多分辨率的脑谱会在测试这些框架思路中非常有用，对启发其改进，以及使用它们进行更多的细节分析上也非常有帮助。

假设2 ——生物学的成本精细结构

可以清楚的是，我们能够画出大脑所有区域的结构差异、动态差异和每个区域所代表内容的差异。当我们找到这些差异，剩下的问题就是，我们是否能够阐释这些由内部产生的成本函数造成的差异，而不是那些在数据输入中产生的差异，或者是反映其他无关成本函数的约束的差异。如果我们能够直接测量不同区域成本函数的各个方面，这样我们就能在不同区域间做出比较。例如，逆强化学习方法可能允许从观察到的可塑性中返回成本函数 (Ng and Russell, 2000)。

此外，当我们开始理解特定成本函数的「神经链接」— 也许按照特定的突触或者神经调节学习规则，基因引导局部布线图案，或者脑区之间的互动模式编码 — 我们也能开始理解观察到的神经回路架构中的差异，在什么时候反映出成本函数中的差异。

我们预计，对于每个不同的学习规则或成本函数，可以存在能识别具体分子类型的细胞或突触。此外，对于每个专门系统，可能有具体分子识别的发育程序，来调整或以其他方式设置其参数。如果进化已经需要调整一个成本函数的参数而不会对其他成本函数造成影响，这就是非常有有意义的事。

大脑产生了多少不同类型的内部训练信号？说到错误信号时，我们不只在讨论多巴胺和血清素，或者其他经典奖励相关的通路。这个错误信号没必要等同于奖励信号，但或许会通过类似于进度下降或者其他的方式用于训练大脑中的特定子网络。将用于驱动优化大脑中特定子电路的成本函数，与哪些是「代价函数」或「效用函数」区分开来非常重要，即预测代理聚集未来奖励的功能。在这两个案例中，可能会使用类似的强化学习机制，但是各自对成本函数的阐释是不同的。虽然它们被广泛延伸到其他研究，但我们还没有强调这里的动物是否具有全球性实用功能(e.g., (O’Reilly et al., 2014a; Bach, 2015))。因为我们认为，即便它们很重要，也只是整个布局的一部分，也就是说大脑不完全是端到端的强化训练系统。

脑图谱的研究进展可能很快可以允许我们对脑中的回路信号类型进行分类，对大脑进行细致的解剖和实现整个大脑奖赏回路的连接，并且详细画出奖励回路是如何与波纹体、皮质、海马体和小脑微电路整合在一起的。这个程序已经被放进苍蝇大脑，这个大脑有 20 个特定类型的多巴胺神经元，连接到解剖中对应的不同蕈形体，训练不同的气味分类器在一组高维气味表示（odor representations）上运行（Aso et al., 2014a,b; Caron et al., 2013; Cohn et al., 2015）。我们已经知道，即使在同一系统内，诸如苍蝇嗅觉回路，一些神经元的布线高度特定的分子编程，而其他布线实际上是随机的，但是这些其他布线也是值得学习的（Aso et al., 2014a）。这些设计原则之间的相互作用，可能会在遗传与学习之间产生多种形式的「分工」。同样的，鸟鸣学习是通过使用依靠与记忆中的大鸟名叫版本进行比较的专门成本函数，进行强化学习的（Fiete et al., 2007），此过程也包括了学习过程中控制鸣声变调的专门结构（Aronov et al., 2011）。这些构成声音学习成本函数构造基础的细节回路图谱正在绘制中（Mandelblat-Cerf et al., 2014）。从简单的系统开始，绘制奖励回路以及它们如何进化和多样化发展应该是可能的。这将在理解系统如何学习的道路上迈出重要一步。

假设3 —— 嵌入一个预结构化体系结构

同样的，鸟鸣学习是通过使用依靠与记忆中的大鸟名叫版本进行比较的专门成本函数，进行强化学习达到的（Fiete et al., 2007），这个过程也涉及了学习过程中控制鸣声变调的专门结构（Aronov et al., 2011）。这些构成声音学习成本函数构造基础的细节回路图谱正在开始绘制中（Mandelblat-Cerf et al., 2014）。从简单的系统开始，绘制奖励回路，以及它们如何进化和多样化发展应该是可能的。这将在理解系统如何学习的道路上迈出重要一步。

神经科学启发下的机器学习

机器学习同样可以被神经科学改变。在大脑中，大量子系统和层级一起运作，生成一个呈现出通用智能的代理（agent）。仅用相对较小的数据量，大脑就可以在广泛问题上表现出智能行为。同样的，在理解大脑上取得的进展也有望改善机器学习。这一部分，我们回顾了之前有关大脑的三个假设，并讨论这些详加阐述的假设将如何有助于打造更加强大的机器学习系统。

假设1—— 存在成本函数

一位好的机器学习从业者应当掌握广泛的优化方法，因地制宜地解决不同问题。我们已经指出，大脑是一种暗含的机器学习机制，历经数百万年的进化。因此，我们应该预期大脑能够横跨许多领域以及数据种类，高效优化成本函数。实际上，我们甚至见证过跨越不同动物种群的、某种大脑结构的收敛演化（Shimizu and Karten, 2013; G¨unt¨urk¨un and Bugnyar, 2016），比如，鸟类大脑仍然没有皮层，但有发达的同源结构——正如试验证实非洲灰鹦鹉有语言技能一样——这种结构是相当复杂智能的来源。似乎有希望实现这一点：通过观察大脑，学会如何实现真正的通用目的优化。

实际上，通过观察大脑可以期望发现多种类型的优化。在硬件层面，大脑明确地设法高效对函数进行优化，尽管低速硬件受制于分子变动，这意味着，机器学习硬件的改进方向应该是更高效的能源利用率。在学习规则的层面，大脑在一种高度非线性的、不可微分的、时间随机的 spiking 系统中解决优化问题，该系统包含海量反馈连接，我们仍然不知道如何针对神经网络，有效解决这个问题。在结构层面，大脑能在仅有极少刺激的基础上，优化某类函数，并在各种时间尺度上运行，而且使用先进的积极学习形式来推断因果结构。

尽管就大脑如何实现优化，我们讨论过很多理论（ (Hinton, 2007, 2016; Bengio et al., 2015a; Balduzzi et al., 2014; Roelfsema et al., 2010; O’Reilly, 1996; O’Reilly et al., 2014a; K¨ording and K¨onig, 2001; Lillicrap et al., 2014)，但是，这些理论仍然是预备性的。因此，第一步就是理解大脑是否真的以近似全梯度下降的方式进行多层信度分配，如果真是这样，它是如何做到的。无论是哪一种方式，我们都可以预期问题的回答会影响到机器学习。如果大脑并不进行某种反向传播（BP），那么，这意味着理解大脑用来避免这样做的技巧，大脑也会受益于此。另一方面，如果大脑不进行 BP，那么，潜在的机制就能支持跨领域的、各种有效优化处理，包括从丰富的时间数据流，通过无监督机制进行学习，而且对于机器学习来说，背后的结构可能具有长期价值。

而且，搜索 BP 的生物合理性形式已经产生了一些有趣的洞见，比如，在 BP 中使用随机反馈权重的可能性(Lillicrap et al., 2014)，或者在混沌、自发的积极循环网络中，意料之外的内 FORCE 学习力量（ (Sussillo and Abbott, 2009)。这一点以及这里讨论的其他发现表明，对于 BP，我们仍然存在某些根本性的不了解——这不但会产生更多具有生物合理性的方式，可资用来训练循环神经网络，从根本上说，这些方式会更加简单，也更加强大。

假设 2——成本函数的生物学精细结构

一个好的机器学习从业者应该接触广泛学习技巧，这意味着能够使用许多不同的成本函数。一些问题需要集簇，一些问题需要提取稀疏变量，还有些问题需要预测质量最大化。大脑也要能够处理许多不同的数据组。同样，大脑因地制宜地使用广泛成本函数解决问题，求生存，也是有意义的。

许多最著名的深度学习的成功，从语言建模（ Sutskever et al., 2011）到视觉（Krizhevsky et al., 2012）到运动控制（motor control)( Levine et al., 2015)，都是端到端的单个任务目标优化驱动的。我们已经突出了一些情况，其中，深度学习已经为成本函数的多样性开启了大门，后者将网络模块塑造成了具有专门作用的角色。我们预期，今后，机器学习会越来越多地采纳这些实践经验。

在计算机视觉方面，我们已经开始看到研究人员会为一个任务（比如ImageNet 分类）重适神经网络训练，然后部署到新任务上，除了它们被训练用来解决的任务，或者提供了更加有限的训练数据的任务(Yosinski et al., 2014; Oquab et al., 2014; Noroozi and Favaro, 2016)）。我们设想这一过程能加以泛化，以系列或并行的方式，各种训练问题，每个都带有一个关联成本函数——可被用来塑造视觉表征。这样训练出来的网络能够被共享，增强以及保留在新任务上。他们能被当做前端，介绍给执行更加复杂目标的系统，或者服务于产生训练其他回路的成本函数（(Watter et al., 2015)。作为一个简单的例子，一个可以区别不同结构架构（比如金字塔或者楼梯等）图片的网络，可被用来评判一个建筑施工（ building-construction）网络。

从科学角度来说，确定成本函数参与生物学大脑的顺序，将让机器学习了解如何利用复杂和分层行为，通过逐个击破的方法（通常被用来解决学习问题、积极学习以及更多问题），来建构系统。

假设3——内嵌于预结构化架构

一个好的机器学习从业者应该掌握广泛算法。动态编程可以高效解决一些问题，哈希算法可以解决另一些问题，有些问题可以通过多层 BP 得到解决。大脑要能解决广泛学习问题，无需进行奢侈地再编程。因此，大脑拥有专门结构，允许快速学会逼近大量算法，就很有意义了。

第一个神经网络是简单的单层系统，或线性或受限非线性（Rashevsky, 1939)。1980s 神经网络研究爆炸式发展，出现了多层网络，接下来是诸如卷积 网络的神经网络（Fukushima, 1980; LeCun and Bengio, 1995）。过去二十年，已经研究出LSTM（ Hochreiter and Schmidhuber, 1997），内容可选址存储器的控制（Weston et al., 2014; Graves et al., 2014）以及增强学习实现的玩游戏（Mnih et al., 2015）。这些网络，尽管在以前看来很新鲜，如今正变成主流算法。还没有迹象表明研发各种新结构化结构的工作正在停止，而且大脑回路的非均质化和模块化意味着，需要各种专门架构来解决举止规范的动物所面对的各种挑战。

大脑将一堆专门结构以一种有用的方式组合起来。在机器学习中，重新解决这个问题可能会很难，因此从观察大脑的运作方式来解决这个问题，就很有吸引力。理解专门结构的宽度以及将它们组合起来的结构，会很十分有用。

进化会使成本函数从优化算法中分离吗？

深度学习方法已经在机器学习领域中刮起了一片热潮。驱动其成功的因素是将学习问题分离成两部分：（1）一种算法，反向传播，允许有效的分布式优化；（2）通过设计一个成本函数和训练过程等方法将给定的问题转化为一个优化问题。如果我们想将深度学习应用到一个新的领域，例如，玩Jeopardy，我们不需要改变优化算法，我们只需要巧妙地设置正确的成本函数。在深度学习中，大多数的工作都是以建立正确的成本函数为重点的。

我们假设，大脑也掌握到了分离优化机制和成本函数的方法。如果神经回路，比如皮质中的神经回路，实现一个通用的优化算法，那么之后该算法的任何改进都将改善全大脑皮质的功能。同时，不同的皮质区，解决不同的问题，所以改变每个皮层区的成本函数相当于提高其性能。因此，将优化问题和成本函数产生问题进行功能性地和进化性地分离，可以进化、产生更好、更快的计算。例如，普通的无监督机制可以结合特定区域基于强化或监督的机制以及错误信号，进来机器学习的很多进展已经发现了一种在单一系统中结合监督和无监督对象的自然方式Rasmus and Berglund，2015）。

这显示出一些有趣的问题：成本函数和优化算法之间的分裂发生在什么时候？这种分离是如何实现的？如何发展成本函数和优化算法的创新？我们的成本函数和学习算法如何把这些与其他动物区分开来。

关于这种区分如何在大脑中形成有很多种可能。六层皮层可能代表着共同的优化算法，但在不同的皮层区域具有不同的成本函数。这种说法不同于所有的皮质区使用一个单一的无监督学习算法实现功能的特异性调整的输入算法的说法。在那个情况下，优化机制和隐含的无监督成本函数将在相同区域（例如，最小化预测误差），只有样本数据来自不同领域，而我们建议，优化机制应是一样的跨区域，但成本函数和训练中的数据则来自不同的区域。因此，包括它的输入和输出数据，成本函数本身就像皮质区的一个辅助输入。之后，一些皮质微电路也许就可以计算被传递到其他皮质微电路的成本函数。

另一种可能性是，在同一线路中，布线和学习规则在某些方面指定一个优化机制，并在跨领域中被相对固定，而另一些指定的成本函数则更多变。后者很可能类似于作为分子和结构配置元素概念的皮质微电路，在现场可编程门阵列类似的细胞（FPGA）（Marcus et al.，A，B），而不是一个同质衬底。这样一种分离的生物性质，如果存在，仍然是一个悬而未决的问题。例如，一个神经元的各个部分可以分别处理优化成本函数的规范，或一个微电路的不同部分，或者是特定类型的细胞，其中一些通过成本函数进行信号处理和其他处理。

结 论

由于大脑的复杂性和可变性，单纯的「自底向上」神经数据分析面可能会面对理解上的挑战（Robinson, 1992; Jonas and Kording, 2016）。理论框架有可能用来约束被评估的假设空间，这使得研究者能首先处理更高等级的系统原理和结构，然后「放大」以处理细节。提出了「自上而下」的理解神经计算框架，包括熵最大化，有效编码，贝叶斯推理的一一逼近，错误预测的最小化，吸引子动力学，模块化，促进符号操作的能力，和许多其他的框架（Bialek, 2002; Bialek et al., 2006; Friston, 2010; Knill and Pouget, 2004; Marcus, 2001; Pinker, 1999）。有趣的是，许多「自上而下」的框架归结为假定大脑只是优化了一个单一的，给定的单一计算架构成本函数。我们归纳的这些提议假定了在发展中演变的异构成本函数组合和专门子系统的多样性。

许多神经科学家致力于搜索「神经码」，即，哪种刺激有助于驱动个体神经元、区域或大脑地区的活动。但是，如果大脑能够一般优化成本函数，那么我们需要意识到，即使是简单的成本函数也能引起发复杂的刺激反应。这有可能导致一系列不同的问题。不同的成本函数确实是有效思考大脑地区不同函数的方法吗？大脑中成本函数的优化究竟是如何发生的，这和人工神经网络的梯度下降实现方式有何区别？什么是目前优化时电路中保持不变的附加约束？优化是如何与结构构架相互作用的？这个构架和我们所勾画的构架相似吗？哪种计算连接到构架，哪种出现在优化中，哪种由极端混合体引起？成本函数在大脑中被明确计算到什么程度，与在本地学习规则中相比？大脑已经进化到可以区分成本函数生成机制和成本函数优化机制了吗？如果是的话，怎么办到的？哪种元层次学习可能是大脑用来在众多选择中学习何时及如何唤醒不同的成本函数或专门系统来处理给定任务的？这个框架的关键机制是什么？神经科学和机器学习之间的更深入的对话能帮助阐释其中的一些问题。

许多机器学习研究者致力于寻找更快的方法，在神经网络中实现端到端的梯度下降。神经科学可能会在多个层次上启发机器学习。大脑中的优化算法已经经历了上百万年的演变。此外，大脑可能已经找到了使用在发展中互相作用的异构函数从而通过引导和塑造无监督学习的结果来简化学习问题的方法。最后，在大脑中进化来的专门结构，可能会告诉我们如何在一个要求在多个时间尺度上解决广泛计算问题的世界中提高学习效率的方法。从神经科学的角度看问题可能会帮助机器学习在一个结构异构化的，只有少量监督数据的世界中，提高到正常智力。

在某种程度上，我们的提议与许多流行的神经计算理论是背道而驰的。这里不只有一个优化机制而可能有许多个，不只有一个成本函数而有一大群，不只一种表示而有任何有用的表示，不只一个异构的结构而有许多这样的结构。这些元素被内部产生的成本函数优化联系到一起，这使得这些系统充分利用彼此。拒绝简单的统一理论和先前广泛的 AI 方法一样。例如，Minsky 和 Papert 的《心智社会》（Society of Mind，Minsky, 1988）和更广泛的基因演化想法及连接系统的内部自举发展（Minsky, 1977）——强调了对内部监视和批评体系、专业通信和储存机制以及简单控制系统的分层结构的需要。

写这些早期作品时，还不是很确定基于梯度优化能否引起强大的特征表示和行为政策。我们的提议可以被视为一个反对简单端到端训练，支持异构方法的重新讨论。换句话说，这个框架之可以被视作提出了一种成本函数及可训练网络「社会」，它允许《Society of Mind》（Minsky, 1988）的内部自助过程。从这个观点看，智力能被许多计算专业结构启用，每个结构被自我发展调节的成本函数训练，其中结构和成本函数都是被类如神经网络超参数的进化优化过的。

©本文由机器之心编译， 转载请联系本公众号授权 。

✄————————————————

加入机器之心（全职记者/实习生）：hr@almosthuman.cn

投稿或寻求报道：editor@almosthuman.cn

广告&商务合作：bd@almosthuman.cn

点击「阅读原文」，下载完整版论文↓↓