自然语言处理之PLSA
上一篇自然语言处理之LSA 介绍了LSA,本文介绍的PLSA(Probabilistic Latent Semantic Analysis, 概率潜在语义分析)由LSA发展而来。LSA使用线性代数方法,对document-word矩阵进行SVD分解。PLSA则使用了一个概率图模型,引入了一个隐变量topic(可以认为是文档的主题),然后进行统计推断。
为何提出PLSA
在语义分析问题中,存在同义词和一词多义这两个严峻的问题,LSA可以很好的解决同义词问题,却无法妥善处理一词多义问题。PLSA则可以同时解决同义词和一词多义两个问题。
概率图模型
我们知道文档(一个句子、一个段落或一篇文章)都有它自己的主题,从大的方面讲有经济、政治、文化、体育、音乐、法律、动漫、游戏、法律等等主题,PLSA模型就引入了一个隐变量topic来表示这个主题。
PLSA的概率图模型如下图所示:

其中 $D$ 表示文档(document),$Z$ 表示主题(topic), $W$ 表示单词(word),其中箭头表示了变量间的依赖关系,比如 $D$ 指向 $Z$,表示一篇文档决定了该文档的主题,$Z$ 指向 $W$ 表示由该主题生成一个单词,方框右下角的字母表示该方框执行的次数,$N$ 表示共有 $N$ 篇文档生成了 $N$ 个主题,$M$ 表示一篇文档生成了 $M$ 个单词。每个文档的单词数可以不同。
PLSA引入了隐藏变量 $Z$,认为 $/lbrace{D,W,Z}/rbrace$ 表示完整的数据集(the complete data set), 而原始的真实数据集 $/lbrace{D,W}/rbrace$ 是不完整的数据集(incomplete data)。
假设 $Z$ 的取值共有 $K$ 个。PLSA模型假设的文档生成过程如下:
1 以 $p(d_i)$ 的概率选择一个文档 $d_i$
2 以 $p(z_k|d_i)$ 的概率选择一个主题 $z_k$
3 以 $p(w_j|z_k)$ 的概率生成一个单词 $w_j$
根据图模型,可以得到下面的式子:
$$
/begin{aligned}
p(d_i,w_j)&=/sum_{k=1}^{K}p(d_i,w_j,z_k) //
&=/sum_{k=1}^{K}p(d_i)p(z_k|d_i)p(w_j|z_k) //
&=p(d_i)/sum_{k=1}^{K}p(z_k|d_i)p(w_j|z_k)
/end{aligned}
$$
第一个等式是对三者的联合概率分布对其中的隐藏变量 $Z$ 的所有取值累加,第二个等式根据图模型的依赖关系将联合概率展开为条件概率,第三个等式只是简单的乘法结合律。这样就计算出了第 $i$ 篇文档与第 $j$ 个单词的联合概率分布。
参数的对数似然
我们可以得到参数的对数似然为:
$$
/begin{aligned}
L&=/sum_{i=1}^N/sum_{j=1}^{M}n(d_i,w_j)logp(d_i,w_j) //
&=/sum_{i=1}^N/sum_{j=1}^{M}n(d_i,w_j)log(p(d_i)/sum_{k=1}^{K}p(z_k|d_i)p(w_j|z_k)) //
&=/sum_{i=1}^{N}n(d_i)logp(d_i)+/sum_{i=1}^N/sum_{j=1}^{M}n(d_i,w_j)log/sum_{k=1}^{K}p(z_k|d_i)p(w_j|z_k)
/end{aligned}
$$
其中 $n(d_i,w_j)$ 表示第 $j$ 个word在第 $i$ 个document中出现的次数。
上式左边一项对于给定的数据集来说是定值,我们只需要使得右边一项取到最大。
我们将 $p(z_k|d_i)$ 和 $p(w_j|z_k)$ 看作是PLSA模型所要求的参数,按照通常的方法,可以通过对参数求导使用梯度下降或牛顿法等方法来求解优化问题,但是这里的参数以求和的形式出现在了对数函数之中,求导结果十分复杂,无法使用通常情况下的方法。
那么应该怎么求解这个最优化问题呢?答案是使用EM算法。
EM算法
这里,我们没有办法直接优化似然性 $L$, 而是通过找到一个辅助函数 $Q$, 使得每次增大辅助函数 $Q$ 的时候确保 $L$ 也能得到增加,图示如下:
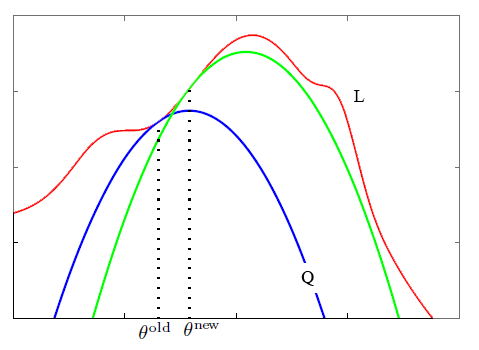
其中红线表示参数的似然性 $L$, 蓝线表示辅助函数 $Q$。
EM算法是一个迭代的过程,分为E步和M步,当未收敛或截断之前,重复执行E-Step和M-Step。
这里先给出EM算法辅助函数 $Q$ 的一般形式:
$$
Q(/theta,/theta^{old})=/sum_{z}p(z|x,/theta_{old})logp(x,z;/theta)
$$
这个$Q$函数的物理意义是完整数据对数似然的期望,上式中 $x$和$z$的组合即为完整数据,对于每个隐含变量 $z$ 的取值,将这个完整数据的对数似然乘上隐含变量的后验概率,最后求和就是完整数据对数似然的期望(expectation of the complete-data log likelihood)。
在E-Step,根据一组旧的参数 $/theta^{old}$ 计算出隐含变量 $z$ 的后验概率,也就确定了一个参数 $/theta$ 的函数 $Q$, 比如这一轮E-Step得到了蓝线表示的$Q$。
然后在M-Step,可以计算出对应于蓝线 $Q$ 函数取得最大值对应的参数 $/theta^{new}$。从而在下一个E-Step得到一个新的 $Q$ 函数(绿线表示)。
可以在图中直观的看到似然性 $L$ 也同时得到了增加。
那么可能有人会产生这样的问题,凭什么 $L$ 难以直接优化,$Q$ 就容易优化,其实这是因为在 $Q$ 中的对数函数中不存在参数的和的形式,而 $L$ 中却存在。
使用EM求解PLSA
上面给出了EM算法 $Q$ 的一般形式,现在给出PLSA中 $Q$ 函数的形式:
$$
/begin{aligned}
Q(/theta,/theta^{old})&=/sum_{i=1}^N/sum_{j=1}^{M}n(d_i,w_j)/sum_{k=1}^{K}p(z_k|d_i,w_j)logp(d_i,w_j,z_k;/theta) //
&=/sum_{i=1}^N/sum_{j=1}^{M}n(d_i,w_j)/sum_{k=1}^{K}p(z_k|d_i,w_j)log[p(d_i)p(z_k|d_i)p(w_j|z_k)]
/end{aligned}
$$
注意到这是因为如前文所说,在本问题中,认为$/lbrace{D,W,Z}/rbrace$ 是完整的数据集。
由于 $p(d_i)/propto{n(d_i)}$ ,$n(d_i)$ 表示第 $i$ 篇文档的单词总数,这一项估计并不重要,因此上式去掉该项,得到:
$$
Q(/theta,/theta^{old})=/sum_{i=1}^N/sum_{j=1}^{M}n(d_i,w_j)/sum_{k=1}^{K}p(z_k|d_i,w_j)log[p(z_k|d_i)p(w_j|z_k)]
$$
可以看到对数中是参数的乘积,不再包含求和的部分。
我们注意到,参数存在下面的两个约束:
$$
/sum_{j=1}^{M}p(w_j|z_k)=1
$$
$$
/sum_{k=1}^{K}p(z_k|d_i)=1
$$
因此可以使用拉格朗日乘子法(Lagrange multiplier)求取使得 $Q$ 函数最大时对应的参数。
写出拉格朗日函数:
$$
Lagrange=Q+/sum_{k=1}^{K}/tau_k(1-/sum_{j=1}^{M}p(w_j|z_k))+/sum_{i=1}^N/rho_i(1-/sum_{k=1}^{K}p(z_k|d_i))
$$
对拉格朗日函数中的 $p(w_j|z_k)$ 求偏导,令其等于零,得到:
$$
/sum_{i=1}^{N}n(d_i,w_j)p(z_k|d_i,w_j)-/tau_{k}p(w_j|z_k)=0, 1/leq{j}/leq{M},1/leq{k}/leq{K}
$$
对该式 $1/leq{j}/leq{M}$ 所有取值下等式两边累加,可以消去 $p(w_j|z_k)$, 从而得到 $/tau_{k}$ 的表达式,回带到上式得到下式:
$$
p(w_j|z_k)=/frac{/sum_{i=1}^{N}n(d_i,w_j)p(z_k|d_i,w_j)}{/sum_{l=1}^{M}/sum_{i=1}^{N}n(d_i,w_l)p(z_k|d_i,w_l)}
$$
对拉格朗日函数中的 $p(z_k|d_i)$ 求偏导,令其等于零,得到:
$$
/sum_{j=1}^{M}n(d_i,w_j)p(z_k|d_i,w_j)-/rho_{i}p(z_k|d_i)=0, 1/leq{i}/leq{N},1/leq{k}/leq{K}
$$
对该式 $1/leq{k}/leq{K}$ 所有取值下等式两边累加,可以消去 $p(z_k|d_i)$, 从而得到 $/rho_i$ 的表达式,回带到上式得到下式:
$$
p(z_k|d_i)=/frac{/sum_{j=1}^{M}n(d_i,w_j)p(z_k|d_i,w_j)}{n(d_i)}
$$
这样就得到了EM算法的M-Step重新估计参数的公式。
那么在E-Step如何计算 $z$ 的后验概率呢?根据下式计算,第一个等式是贝叶斯法则,第二个等式是根据图模型将联合概率展开,第三个等式是分子分母同时除以一个因子。
$$
/begin{aligned}
p(z_k|d_i,w_j)&=/frac{p(d_i,w_j,z_k)}{p(d_i,w_j)} //
&=/frac{p(d_i)p(z_k|d_i)p(w_j|z_k)}{/sum_{l=1}^{K}p(d_i)p(z_l|d_i)p(w_j|z_l)} //
&=/frac{p(z_k|d_i)p(w_j|z_k)}{/sum_{l=1}^{K}p(z_l|d_i)p(w_j|z_l)}
/end{aligned}
$$
那么何时停止算法呢?一种方法是计算对数似然性,当这个值的变化小于某个阈值时认为已经收敛;另一种方法可以固定迭代次数,进行截断,避免过拟合。
如何实现PLSA
代码中使用 $/lambda_{ik}$ ($lamda[i,k]$)表示参数 $p(z_k|d_i)$, 用 $/theta_{kj}$ ($theta[k,j]$)表示参数 $p(w_j|z_k)$, 用 $p_{ijk}$ ($p[i,j,k]$)表示隐藏变量的后验概率 $p(z_k|d_i,w_j)$。
参数 $/theta$ 和 $/lambda$ 起初使用随机值初始化并归一化到和为1。
这里需要一提的是,隐变量取值个数 $K$,根据不同的数据集,为了获得较好的结果,是需要随着数据的变换适当调整的。
# 读数据集
file = codecs.open('dataset.txt','r','utf-8')
documents = [document.strip() for document in file]
file.close()
# 文档总数
N = len(documents)
# topic数,不同数据集应适当调整
K = 3
#==============================================================================
# 统计词语在每篇文档中的出现次数以及总词数
#==============================================================================
# map类型,键是word,值是word在全部documents中出现的总次数
wordCount = {}
# list类型,每个元素是一个map类型对象,键是word,值是word在对应的document中出现的次数
wordCountPerDocument = [];
# 要去除的标点符号的正则表达式
punctuationRegex = '[,.;"?!#-_…()`|“”‘]+'
stopwords = ['a','an', 'after', 'also', 'and', 'as', 'be', 'being', 'but', 'by', 'd', 'for', 'from', 'he', 'her', 'his', 'in', 'is', 'more', 'of', 'often', 'the', 'to', 'who', 'with', 'people']
for d in documents:
words = d.split()
wordCountCurrentDoc = {}
for w in words:
# 过滤stopwords并小写化
w = re.sub(punctuationRegex, '', w.lower())
if len(w)<=1 or re.search('http', w) or re.search('[0-9]', w) or w in stopwords:
continue
# 否则统计该词出现次数
if w in wordCount:
wordCount[w] += 1
else:
wordCount[w] = 1
if w in wordCountCurrentDoc:
wordCountCurrentDoc[w] += 1
else:
wordCountCurrentDoc[w] = 1
wordCountPerDocument.append(wordCountCurrentDoc);
#==============================================================================
# 构造词表
#==============================================================================
# map类型,键是word,值是word的编号
dictionary = {}
# map类型,键是word的编号,值是word
dictionaryReverse = {}
index = 0;
for word in wordCount.keys():
if wordCount[word] > 1:
dictionary[word] = index;
dictionaryReverse[index] = word;
index += 1;
# 词表长度
M = len(dictionary)
#==============================================================================
# 构造document-word矩阵
#==============================================================================
X = zeros([N, M], int8)
for word in dictionary.keys():
j = dictionary[word]
for i in range(0, N):
if word in wordCountPerDocument[i]:
X[i, j] = wordCountPerDocument[i][word];
#==============================================================================
# 初始化参数
#==============================================================================
# lamda[i, j] : p(zj|di)
lamda = random([N, K])
for i in range(0, N):
normalization = sum(lamda[i, :])
for j in range(0, K):
lamda[i, j] /= normalization;
# theta[i, j] : p(wj|zi)
theta = random([K, M])
for i in range(0, K):
normalization = sum(theta[i, :])
for j in range(0, M):
theta[i, j] /= normalization;
#==============================================================================
# 定义隐变量的后验概率的矩阵表示
#==============================================================================
# p[i, j, k] : p(zk|di,wj)
p = zeros([N, M, K])
#==============================================================================
# E-Step
#==============================================================================
def EStep():
for i in range(0, N):
for j in range(0, M):
denominator = 0;
for k in range(0, K):
p[i, j, k] = theta[k, j] * lamda[i, k];
denominator += p[i, j, k];
if denominator == 0:
for k in range(0, K):
p[i, j, k] = 0;
else:
for k in range(0, K):
p[i, j, k] /= denominator;
#==============================================================================
# M-Step
#==============================================================================
def MStep():
# 更新参数theta
for k in range(0, K):
denominator = 0
for j in range(0, M):
theta[k, j] = 0
for i in range(0, N):
theta[k, j] += X[i, j] * p[i, j, k]
denominator += theta[k, j]
if denominator == 0:
for j in range(0, M):
theta[k, j] = 1.0 / M
else:
for j in range(0, M):
theta[k, j] /= denominator
# 更新参数lamda
for i in range(0, N):
for k in range(0, K):
lamda[i, k] = 0
denominator = 0
for j in range(0, M):
lamda[i, k] += X[i, j] * p[i, j, k]
denominator += X[i, j];
if denominator == 0:
lamda[i, k] = 1.0 / K
else:
lamda[i, k] /= denominator
#==============================================================================
# EM algorithm
#==============================================================================
for i in range(0, 20):
EStep()
MStep()
PLSA实验结果
首先,先用实现LSA时使用的海贼王wikipedia上的数据做个实验。设置 $K=3$。
实验数据见下图:

实验结果如下,抽取了每个主题下出现概率最大的10个单词,(即 $p(w_j|z_k)$)。

我们可以看到三个主题的第一个词分别为nami,luffy,zoro,恰好是三个主角的名字,并且每个对应的主题下恰好是描述该主角的单词,可以看到结果非常的好。
需要注意,多次运行,得到的结果不能保证每个主题词的概率顺序不变,但有哪些词基本不会有太大区别。
下面再用一个大一些的数据集做一下实验。结果如下。

这一次使用了更多的文本,设置 $K=10$。
可以看到主题2很明显是关于恶魔果实,主题6关于霸气,主题5关于地理设定,主题4关于阿拉巴斯坦,主题7关于司法岛草帽海贼团对世界政府宣战,主题8关于luffy在德雷斯罗塞击败多弗朗明哥,主题1关于象岛,主题9关于罗杰开启大航海时代。
经过实验发现,每一次实验会跑出不同的结果,出现的词会发生变化,比如图片中所示的这次试验在主题4中概率前10的词没有出现克洛克达尔这个词,而我发现有的时候是会出现的,这说明EM算法随机的初始值可能会导致词语在某个主题的概率的排名发生变化,但基本上主题是比较稳定的。
参考资料
1 Unsupervised Learning by Probabilistic Latent Semantic Analysis by Thomas Hofmann
2 Pattern Recognition and Machine Learning Chapter 9
3 wikipedia Lagrange multiplier
完整代码(包括计算似然性以及输出主题词top10)以及文中两个实验的数据已托管至 github











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

