球面拟合算法
引言
在传感器数据融合以及工业测量中,常常需要对已知的数据或者是已知的结构的特征参数进行检测,来评估数据的信噪比或者结构的质量是否符合产品的需求。一般的,可以通过记录大量数据或者通过结构的离散点,来反解出它的特征参数。 以球面为例,这些特征参数可以是球的半径,或者是球心等。对于球体拟合算法,通常有代数拟合和几何拟合。在本例中,以一般的代数拟合方法为主进行介绍。
原理分析
以下图的数据为例,我们可以明显看出这些数据“可能”是一个球体,那么我们应该如何来得到这个球体的半径以及球心?
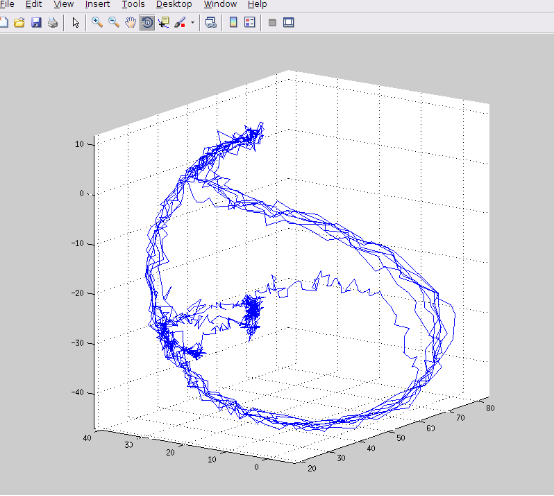
从如此多的数据中很明显可以看到,最后的执行方程组肯定是超定方程组。正常来看,超定方程组是没有解的,但在数值计算领域我们可以以最优解的形式来获得我们想要的参数。正所谓,有总比没有好,迟到总比不到好,是吧。
话不多说,原始数据经过剔除异常点以及滤波之后,我们假设这些离散点为
Pi = (Xi,Yi,Zi), i = 1,2,…,n
假如球的球心m为 (a,b,c),球的半径为 r,则球的标准方程为
(x-a)^2 + (y-b)^2 + (z-c)^2 = r^2
以 Di 表示离散点 Pi 到 m 的距离,即
Di^2 = (Xi-a)^2 + (Yi-b)^2 + (Zi-c)^2, i = 1,2,…,n。
令残差平方和 S = 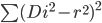 其中 i = 1,2,…,n。
其中 i = 1,2,…,n。
为了选取最合适的让该等式”尽量成立”,只需要让 S 为最小值即可。也就是说,b` = argmin(S)。而且很明显,S 肯定存在大于或等于 0 的极小值。由逼近算法可以罗列出超定方程组,在这里,我们将球的标准方程展开然后代入 S 中,将 S 对其中的未知数求偏导,令偏导为 0,得到极值点,比较之后即可得到最小值。由于解方程是比较基础的内容,本例中就不罗列出来了。
这个时候,就可以将 b` 中的数据直接代入球的标准方程,看看是否得到了我们想要的球面。一般的,可以直接得到比较好的球面了。
误差分析
这个时候还没有结束,我们还需要对我们所得到的球面进行评定,看看是否误差在允许的范围之内,这个范围取决于个人或者组织对产品的定义。我们可以将所得到的最优解 b` 以及离散点Pi的均方误差作为评定的参考,假如均方误差不在允许范围之内,可以再次进行剔除异常值还有滤波,一直迭代,直到数据满足要求。
原理扩展
从上述例子中,我们可以知道,该算法不仅可以从大量已知数据得出最优解,也可以从四个不共面的点来确定一球面,甚至可以通过结构的球冠来得到最匹配的球面。
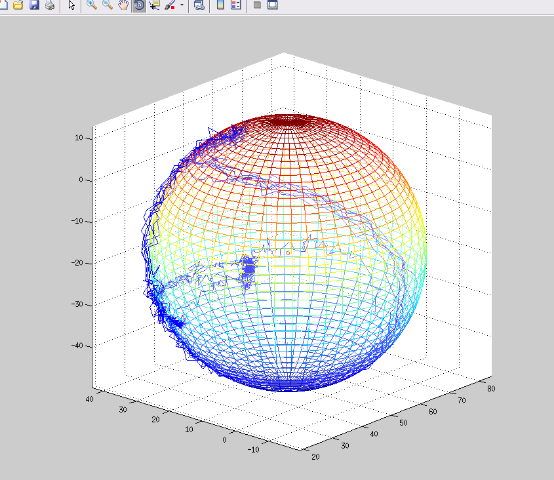
下图是经过剔除异常值并且滤波之后,由上述逼近算法拟合得到的最优解。
结语
这个案例还比较容易,因为仅有 4 个未知量,而且也不需要考虑三维空间旋转。如果大伙搞懂了这个,下次再来给大伙讲讲二次曲面/椭球拟合算法(结合三维空间旋转,大概 10 个未知数)或者扩展卡尔曼滤波结合四元数进行姿态解算。
参考资料
《概率论与数理统计》(第 4 版)盛骤











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

