转载

学习笔记：使用 OpenCV 识别 QRCode

背景

识别二维码的项目数不胜数，每次都是开箱即用，方便得很。

这次想用 OpenCV 从零识别二维码，主要是温习一下图像处理方面的基础概念，熟悉 OpenCV 的常见操作，以及了解二维码识别和编码的基本原理。

作者本人在图像处理方面还是一名新手，采用的方法大多原始粗暴，如果有更好的解决方案欢迎指教。

QRCode

二维码有很多种，这里我选择的是比较常见的 QRCode 作为探索对象。QRCode 全名是 Quick Response Code，是一种可以快速识别的二维码。

尺寸

QRCode 有不同的 Version ，不同的 Version 对应着不同的尺寸。将最小单位的黑白块称为 module ，则 QRCode 尺寸的公式如下：

Version V = ((V-1)*4 + 21) ^ 2 modules

常见的 QRCode 一共有40种尺寸：

Version 1 : 21 * 21 modules
Version 2 : 25 * 25 modules
…
Version 40: 177 * 177 modules

组成

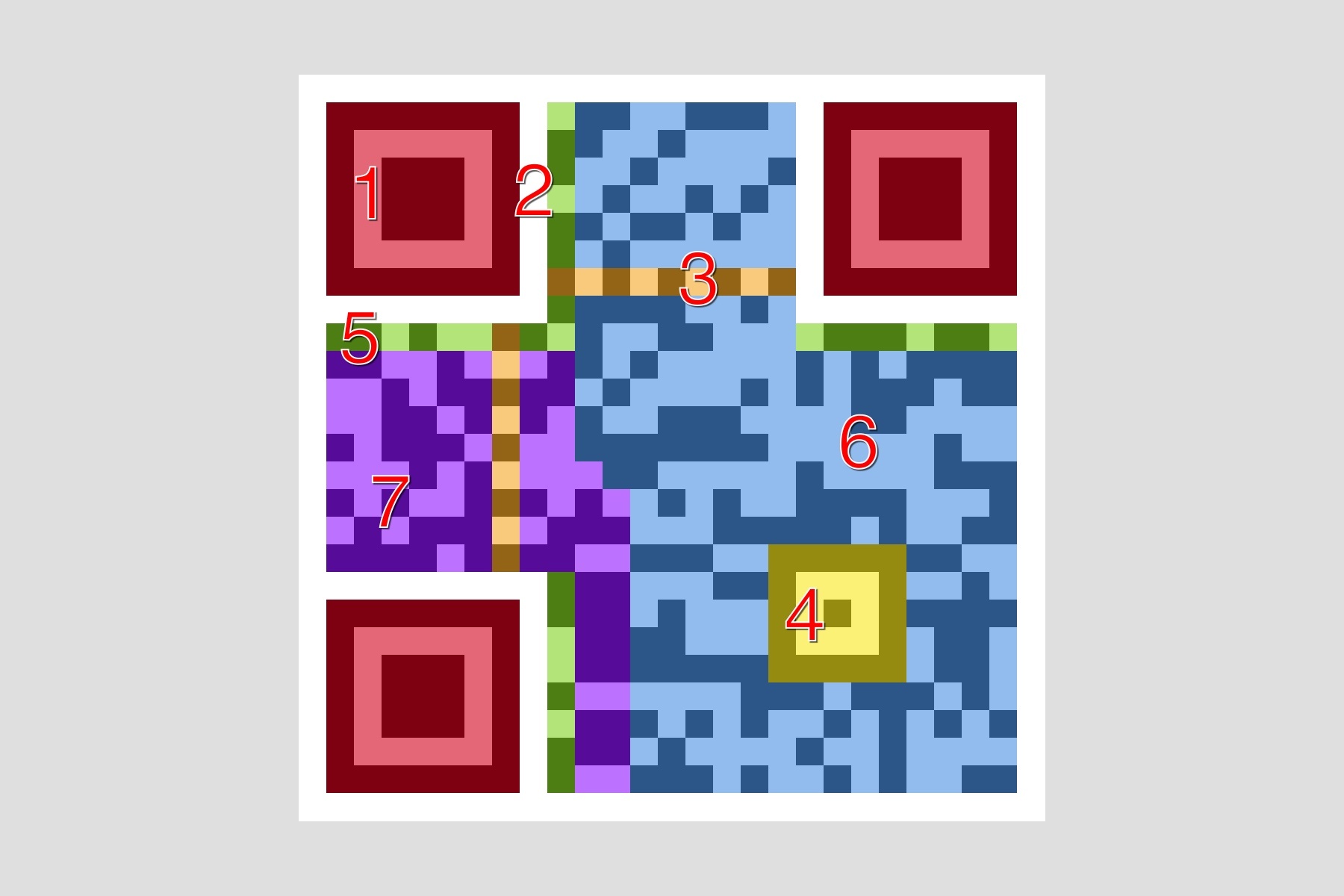
学习笔记：使用 OpenCV 识别 QRCode

QRCode 主要由以下部分组成：

1 - Position Detection Pattern：位于三个角落，可以快速检测二维码位置。
2 - Separators：一个单位宽的分割线，提高二维码位置检测的效率。
3 - Timing Pattern：黑白相间，用于修正坐标系。
4 - Alignment Patterns：提高二维码在失真情况下的识别率。
5 - Format Information：格式信息，包含了错误修正级别和掩码图案。
6 - Data：真正的数据部分。
7 - Error Correction：用于错误修正，和 Data 部分格式相同。

具体的生成原理和识别细节可以阅读文末的参考文献，比如耗子叔的这篇《二维码的生成细节和原理》。

由于二维码的解码步骤比较复杂，而本次学习重点是数字图像处理相关的内容，所以本文主要是解决二维码的识别定位问题，数据解码的工作交给第三方库（比如 ZBAR）完成。

OpenCV

在开始识别二维码之前，还需要补补课，了解一些图像处理相关的基本概念。

contours

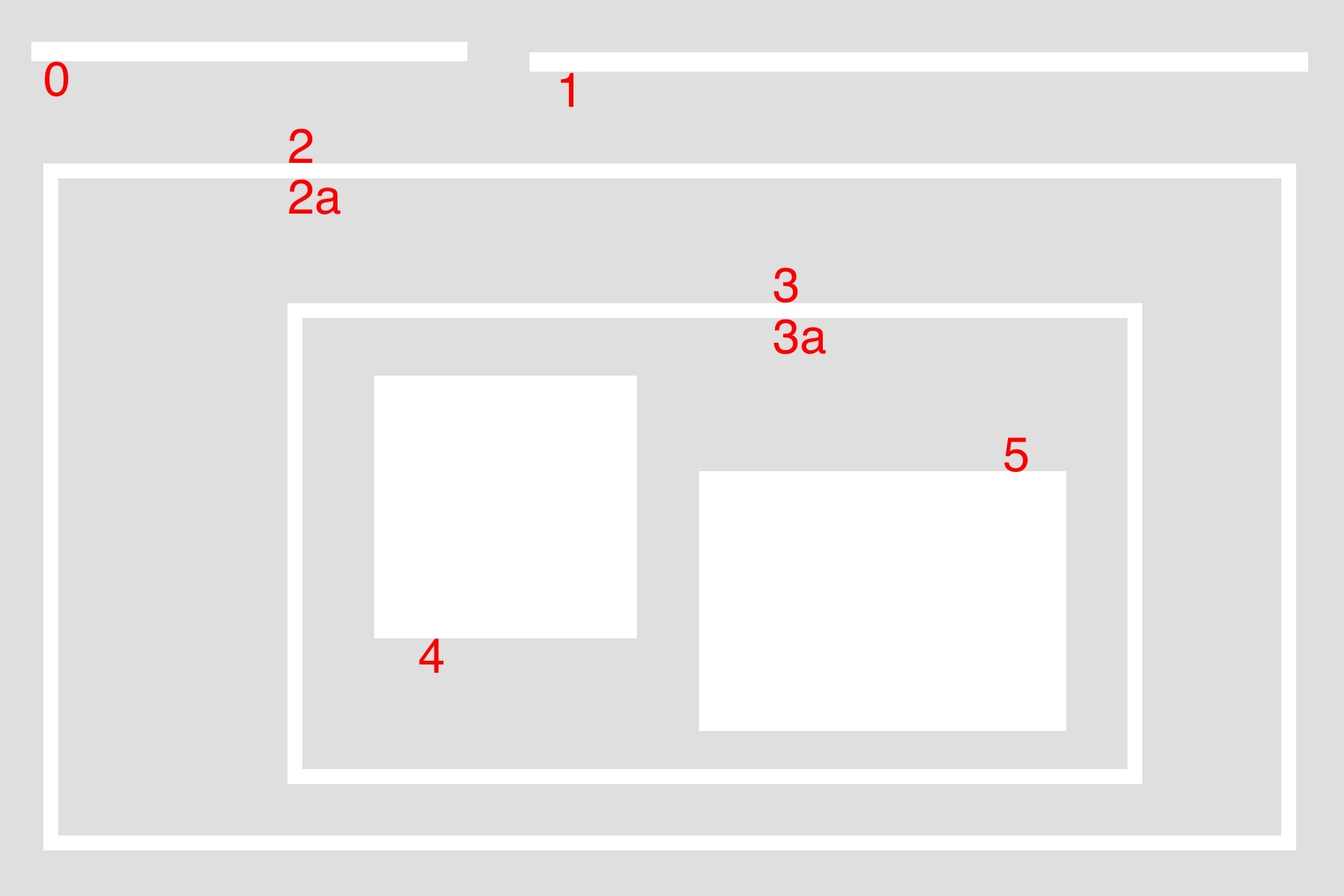
轮廓（contour）可以简单理解为一段连续的像素点。比如一个长方形的边，比如一条线，比如一个点，都属于轮廓。而轮廓之间有一定的层级关系，以下图为例：

学习笔记：使用 OpenCV 识别 QRCode

主要说明以下概念：

external & internal：对于最大的包围盒而言，2 是外部轮廓（external），2a 是内部轮廓（internal）。
parent & child：2 是 2a 的父轮廓（parent），2a 是 2 的子轮廓（child），3 是 2a 的子轮廓，同理，3a 是 3 的子轮廓，4 和 5 都是 3a 的子轮廓。
external | outermost：0、1、2 都属于最外围轮廓（outermost）。
hierarchy level：0、1、2 是同一层级（same hierarchy），都属于 hierarchy-0 ，它们的第一层子轮廓属于 hierarchy-1 。
first child：4 是 3a 的第一个子轮廓（first child）。实际上 5 也可以，这个看个人喜好了。

在 OpenCV 中，通过一个数组表达轮廓的层级关系：

[Next, Previous, First_Child, Parent]

Next：同一层级的下一个轮廓。在上图中， 0 的 Next 就是 1 ，1 的 Next 就是 2 ，2 的 Next 是 -1 ，表示没有下一个同级轮廓。
Previous：同一层级的上一个轮廓。比如 5 的 Previous 是 4， 1 的 Previous 就是 0 ，0 的 Previous 是 -1 。
First_Child：第一个子轮廓，比如 2 的 First_Child 就是 2a ，像 3a 这种有两个 Child ，只取第一个，比如选择 4 作为 First_Child 。
Parent：父轮廓，比如 4 和 5 的 Parent 都是 3a ，3a 的 Parent 是 3 。

关于轮廓层级的问题，参考阅读：《Tutorial: Contours Hierarchy》

findContours

了解了 contour 相关的基础概念之后，接下来就是在 OpenCV 里的具体代码了。

findContours 是寻找轮廓的函数，函数定义如下：

cv2.findContours(image, mode, method) → image, contours, hierarchy

其中：

image：资源图片，8 bit 单通道，一般需要将普通的 BGR 图片通过 cvtColor 函数转换。
mode：边缘检测的模式，包括：
- CV_RETR_EXTERNAL：只检索最大的外部轮廓（extreme outer），没有层级关系，只取根节点的轮廓。
- CV_RETR_LIST：检索所有轮廓，但是没有 Parent 和 Child 的层级关系，所有轮廓都是同级的。
- CV_RETR_CCOMP：检索所有轮廓，并且按照二级结构组织：外轮廓和内轮廓。以前面的大图为例，0、1、2、3、4、5 都属于第0层，2a 和 3a 都属于第1层。
- CV_RETR_TREE：检索所有轮廓，并且按照嵌套关系组织层级。以前面的大图为例，0、1、2 属于第0层，2a 属于第1层，3 属于第2层，3a 属于第3层，4、5 属于第4层。
method：边缘近似的方法，包括：
- CV_CHAIN_APPROX_NONE：严格存储所有边缘点，即：序列中任意两个点的距离均为1。
- CV_CHAIN_APPROX_SIMPLE：压缩边缘，通过顶点绘制轮廓。

drawContours

drawContours 是绘制边缘的函数，可以传入 findContours 函数返回的轮廓结果，在目标图像上绘制轮廓。函数定义如下：

Python: cv2.drawContours(image, contours, contourIdx, color) → image

其中：

image：目标图像，直接修改目标的像素点，实现绘制。
contours：需要绘制的边缘数组。
contourIdx：需要绘制的边缘索引，如果全部绘制则为 -1。
color：绘制的颜色，为 BGR 格式的 Scalar 。
thickness：可选，绘制的密度，即描绘轮廓时所用的画笔粗细。
lineType: 可选，连线类型，分为以下几种：
- LINE_4：4-connected line，只有相邻的点可以连接成线，一个点有四个相邻的坑位。
- LINE_8：8-connected line，相邻的点或者斜对角相邻的点可以连接成线，一个点有四个相邻的坑位和四个斜对角相邻的坑位，所以一共有8个坑位。
- LINE_AA：antialiased line，抗锯齿连线。
hierarchy：可选，如果需要绘制某些层级的轮廓时作为层级关系传入。
maxLevel：可选，需要绘制的层级中的最大级别。如果为1，则只绘制最外层轮廓，如果为2，绘制最外层和第二层轮廓，以此类推。

moments

矩（moment）起源于物理学的力矩，最早由阿基米德提出，后来发展到统计学，再后来到数学进行归纳。本质上来讲，物理学和统计学的矩都是数学上矩的特例。

物理学中的矩表示作用力促使物体绕着支点旋转的趋向，通俗理解就像是拧螺丝时用的扭转的力，由矢量和作用力组成。

数学中的矩用来描述数据分布特征的一类数字特征，例如：算术平均数、方差、标准差、平均差，这些值都是矩。在实数域上的实函数 f(x) 相对于值 c 的 n 阶矩为：

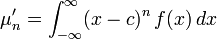
学习笔记：使用 OpenCV 识别 QRCode

常用的矩有两类：

原点矩（raw moment）：相对原点的矩，即当 c 为 0 的时候。1阶原点矩为期望，也成为中心。
中心矩（central moment）：相对于中心点的矩，即当 c 为 E(x) 的时候。1阶中心矩为0，2阶中心矩为方差。

到了图像处理领域，对于灰度图（单通道，每个像素点由一个数值来表示）而言，把坐标看成二维变量 (X, Y)，那么图像可以用二维灰度密度函数 I(x, y) 来表示。

简单来讲，图像的矩就是图像的像素相对于某个点的分布情况统计，是图像的一种特征描述。

raw moment

图像的原点矩（raw moment）是相对于原点的矩，公式为：

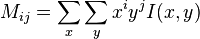
学习笔记：使用 OpenCV 识别 QRCode

对于图像的原点矩而言：

M₀₀ 相当于权重系数为 1 。将所有 I(x, y) 相加，对于二值图像而言，相当于将每个点记为 1 然后求和，也就是图像的面积；对于灰度图像而言，则是图像的灰度值的和。
M₁₀ 相当于权重为 x 。对二值图像而言，相当于将所有的 x 坐标相加。
M₀₁ 相当于权重为 y 。对二值图像而言，相当于将所有的 y 坐标相加。
图像的几何中心（centroid）等于 (M₁₀ / M₀₀ , M₀₁ / M₀₀)。

central moment

图像的中心矩（central moment）是相对于几何中心的矩，公式为：

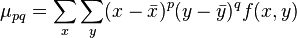
学习笔记：使用 OpenCV 识别 QRCode

可以看到，中心矩表现的是图像相对于几何中心的分布情况。一个通用的描述中心矩和原点矩关系的公式是：

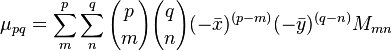
学习笔记：使用 OpenCV 识别 QRCode

中心矩在图像处理中的一个应用便是寻找不变矩（invariant moments），这是一个高度浓缩的图像特征。

所谓的不变性有三种，分别对应图像处理中的三种仿射变换：

平移不变性（translation invariants）：中心矩本身就具有平移不变性，因为它是相对于自身的中心的分布统计，相当于是采用了相对坐标系，而平移改变的是整体坐标。
缩放不变性（scale invariants）：为了实现缩放不变性，可以构造一个规格化的中心矩，即将中心矩除以 (1+(i+j)/2) 阶的0阶中心矩，具体公式见《Wiki: scale invariants》。
旋转不变性（rotation invariants）：通过2阶和3阶的规格化中心矩可以构建7个不变矩组，构成的特征量具有旋转不变性。具体可以看《Wiki: rotation invariants》。

Hu moment 和 Zernike moment 之类的内容就不继续展开了，感兴趣的可以翻阅相关文章。

OpenCV + QRCode

接下来就是将 QRCode 和 OpenCV 结合起来的具体使用了。

初步构想的识别步骤如下：

加载图像，并且进行一些预处理，比如通过高斯模糊去噪。
通过 Canny 边缘检测算法，找出图像中的边缘
寻找边缘中的轮廓，将嵌套层数大于 4 的边缘找出，得到 Position Detection Pattern 。
如果上一步得到的结果不为 3 ，则通过 Timing Pattern 去除错误答案。
计算定位标记的最小矩形包围盒，获得三个最外围顶点，算出第四个顶点，从而确定二维码的区域。
计算定位标记的几何中心，连线组成三角形，从而修正坐标，得到仿射变换前的 QRCode 。

在接下来的内容里，将会尝试用 OpenCV 识别下图中的二维码：

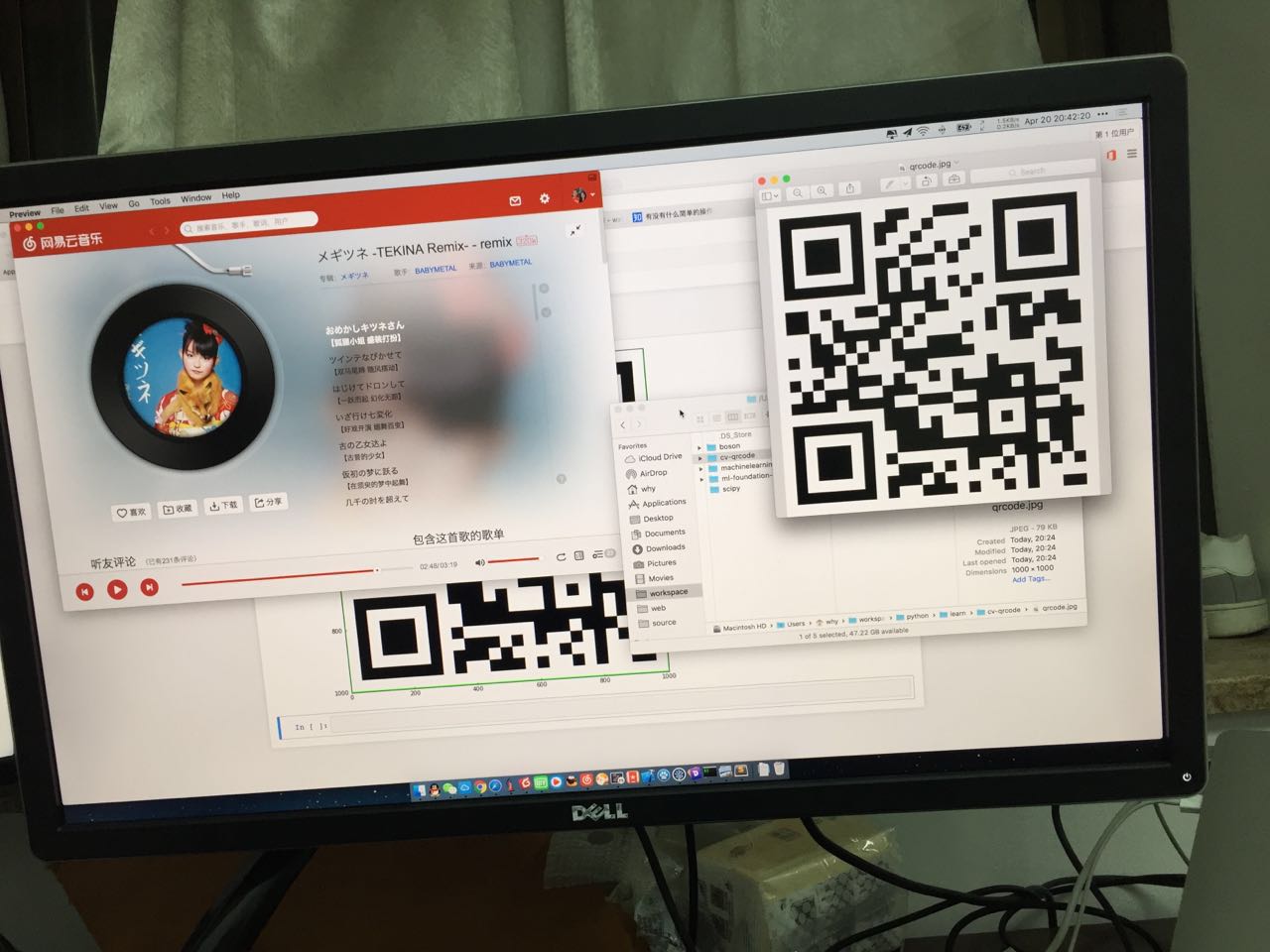
学习笔记：使用 OpenCV 识别 QRCode

加载图像

首先加载图像，并通过 matplotlib 显示图像查看效果：

%matplotlib inline
import cv2
from matplotlib import pyplot as plt
import numpy as np

def show(img, code=cv2.COLOR_BGR2RGB):
    cv_rgb = cv2.cvtColor(img, code)
    fig, ax = plt.subplots(figsize=(16, 10))
    ax.imshow(cv_rgb)
    fig.show()

img = cv2.imread('1.jpg')
show(img)

OpenCV 中默认是 BGR 通道，通过 cvtColor 函数将原图转换成灰度图：

img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

边缘检测

有了灰度图之后，接下来用 Canny 边缘检测算法检测边缘。

Canny 边缘检测算法主要是以下几个步骤：

用高斯滤波器平滑图像去除噪声干扰（低通滤波器消除高频噪声）。
生成每个点的亮度梯度图（intensity gradients），以及亮度梯度的方向。
通过非极大值抑制（non-maximum suppression）缩小边缘宽度。非极大值抑制的意思是，只保留梯度方向上的极大值，删除其他非极大值，从而实现锐化的效果。
通过双阈值法（double threshold）寻找潜在边缘。大于高阈值为强边缘（strong edge），保留；小于低阈值则删除；不大不小的为弱边缘（weak edge），待定。
通过迟滞现象（Hysteresis）处理待定边缘。弱边缘有可能是边缘，也可能是噪音，判断标准是：如果一个弱边缘点附近的八个相邻点中，存在一个强边缘，则此弱边缘为强边缘，否则排除。

在 OpenCV 中可以直接使用 Canny 函数，不过在那之前要先用 GaussianBlur 函数进行高斯模糊：

img_gb = cv2.GaussianBlur(img_gray, (5, 5), 0)

接下来使用 Canny 函数检测边缘，选择 100 和 200 作为高低阈值：

edges = cv2.Canny(img_gray, 100 , 200)

执行结果如下：

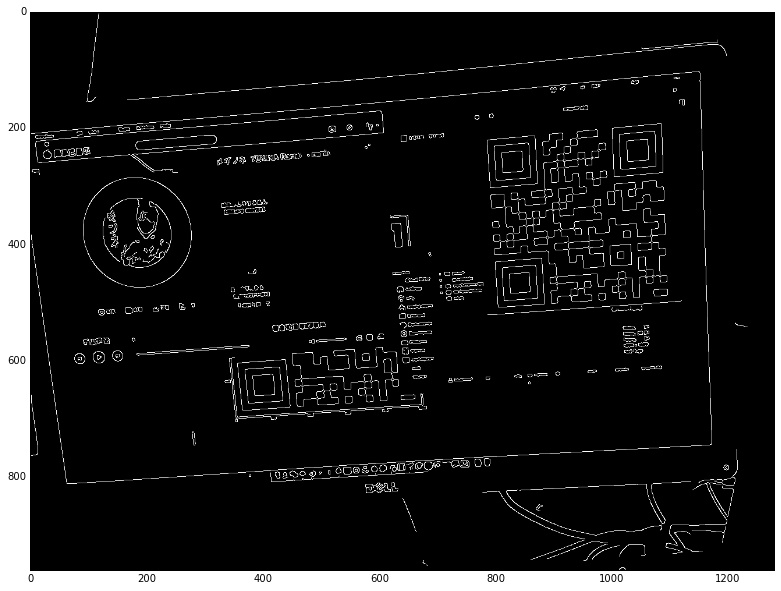
学习笔记：使用 OpenCV 识别 QRCode

可以看到图像中的很多噪音都被处理掉了，只剩下了边缘部分。

寻找定位标记

有了边缘之后，接下来就是通过轮廓定位图像中的二维码。二维码的 Position Detection Pattern 在寻找轮廓之后，应该是有6层（因为一条边缘会被识别出两个轮廓，外轮廓和内轮廓）：

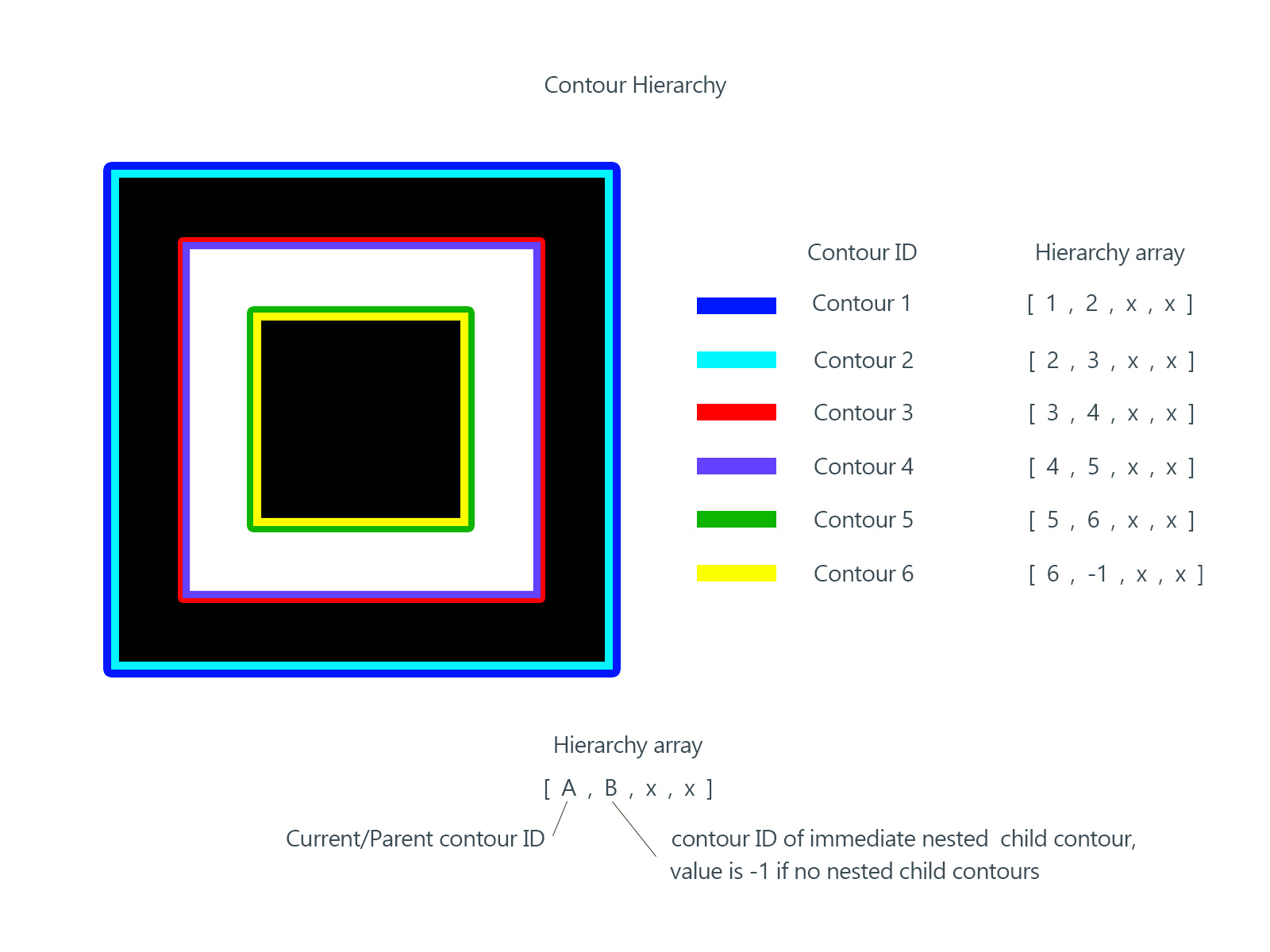
学习笔记：使用 OpenCV 识别 QRCode

所以，如果简单处理的话，只要遍历图像的层级关系，然后嵌套层数大于等于5的取出来就可以了：

img_fc, contours, hierarchy = cv2.findContours(edges, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)

hierarchy = hierarchy[0]
found = []
for i in range(len(contours)):
    k = i
    c = 0
    while hierarchy[k][2] != -1:
        k = hierarchy[k][2]
        c = c + 1
    if c >= 5:
        found.append(i)

for i in found:
    img_dc = img.copy()
    cv2.drawContours(img_dc, contours, i, (0, 255, 0), 3)
    show(img_dc)

绘制结果如下：

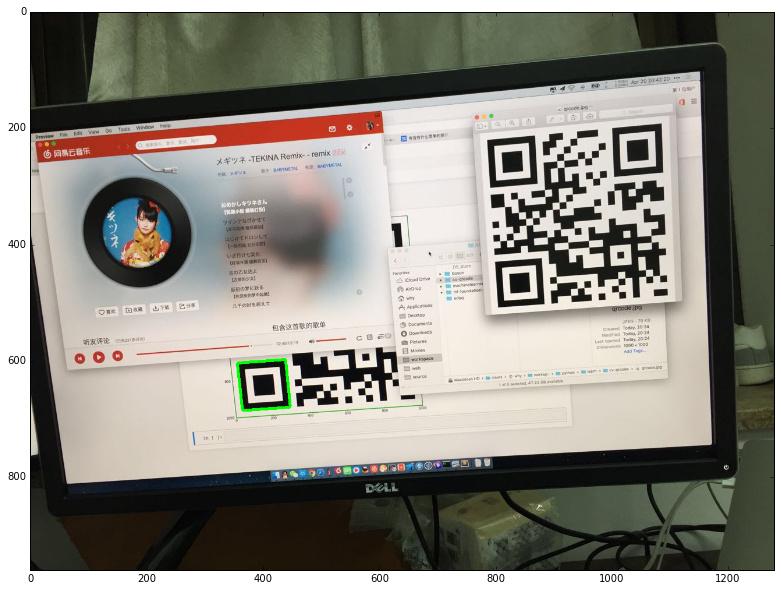
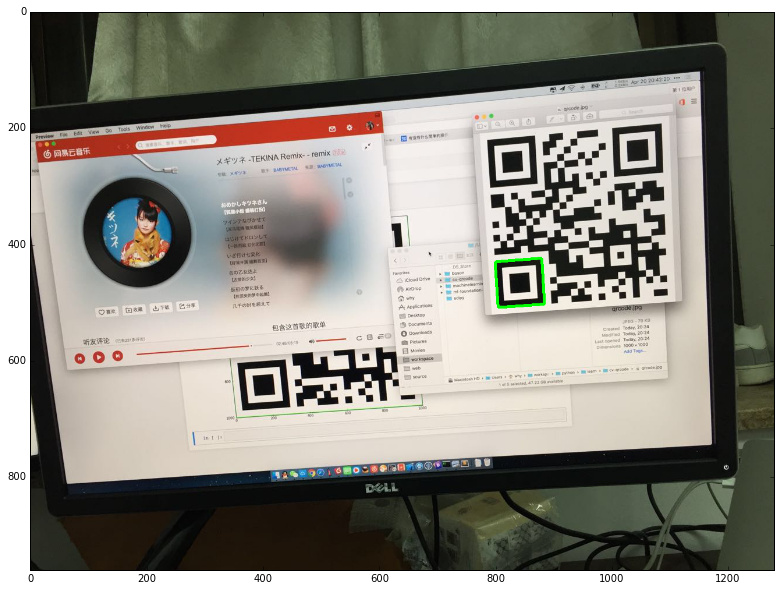
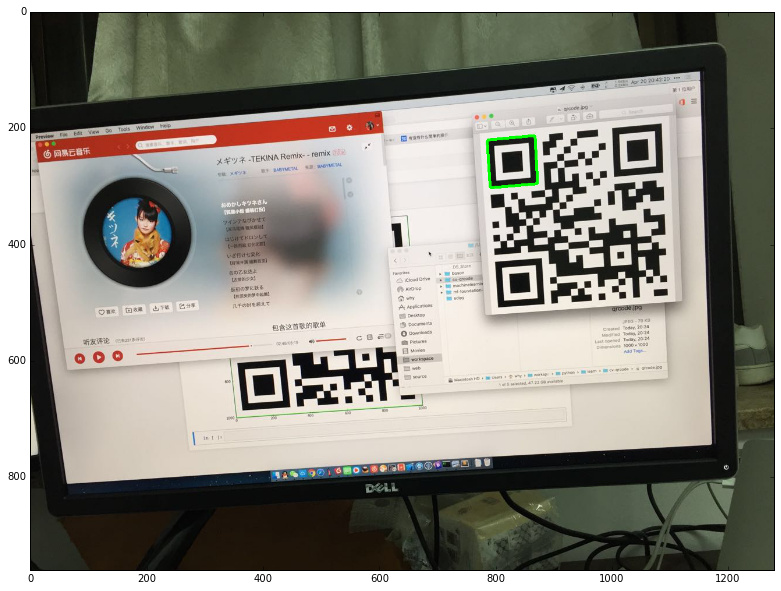
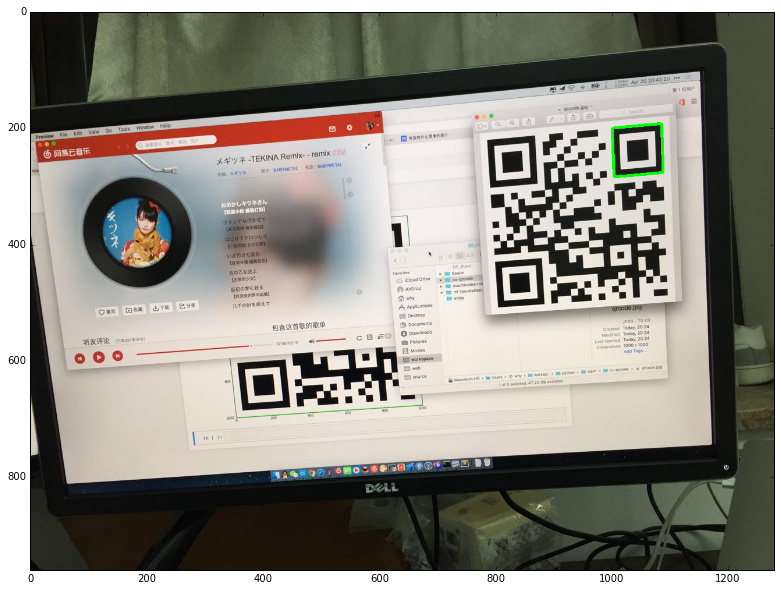
学习笔记：使用 OpenCV 识别 QRCode

定位筛选

接下来就是把所有找到的定位标记进行筛选。如果刚好找到三个那就可以直接跳过这一步了。然而，因为这张图比较特殊，找出了四个定位标记，所以需要排除一个错误答案。

讲真，如果只靠三个 Position Detection Pattern 组成的直角三角形，是没办法从这四个当中排除错误答案的。因为，一方面会有形变的影响，比如斜躺着的二维码，本身三个顶点连线就不是直角三角形；另一方面，极端情况下，多余的那个标记如果位置比较凑巧的话，完全和正确结果一模一样，比如下面这种情况：

学习笔记：使用 OpenCV 识别 QRCode

所以我们需要 Timing Pattern 的帮助，也就是定位标记之间的黑白相间的那两条黑白相间的线。解决思路大致如下：

将4个定位标记两两配对
将他们的4个顶点两两连线，选出最短的那两根
如果两根线都不符合 Timing Pattern 的特征，则出局

寻找定位标记的顶点

找的的定位标记是一个轮廓结果，由许多像素点组成。如果想找到定位标记的顶点，则需要找到定位标记的矩形包围盒。先通过 minAreaRect 函数将检查到的轮廓转换成最小矩形包围盒，并且绘制出来：

draw_img = img.copy()
for i in found:
    rect = cv2.minAreaRect(contours[i])
    box = cv2.boxPoints(rect)
    box = np.int0(box)
    cv2.drawContours(draw_img,[box], 0, (0,0,255), 2)
show(draw_img)

绘制如下：

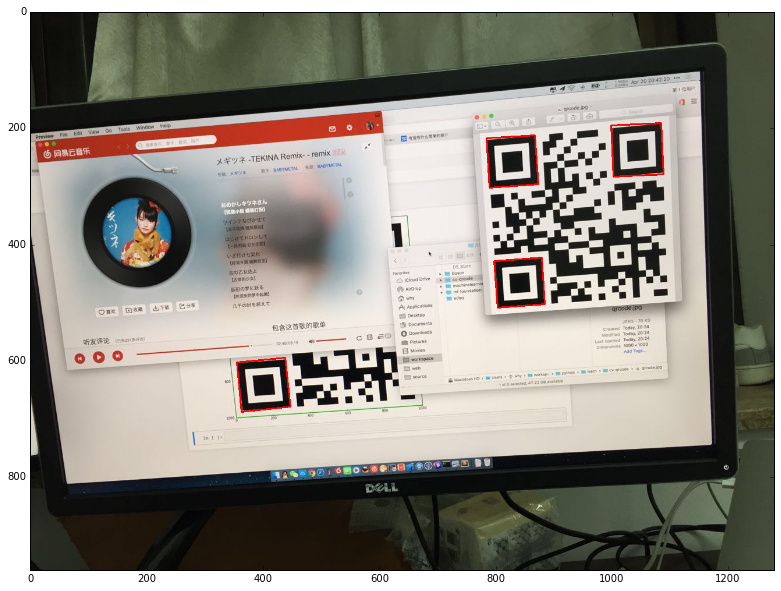
学习笔记：使用 OpenCV 识别 QRCode

这个矩形包围盒的四个坐标点就是顶点，将它存储在 boxes 中：

boxes = []
for i in found:
    rect = cv2.minAreaRect(contours[i])
    box = cv2.boxPoints(rect)
    box = np.int0(box)
    box = map(tuple, box)
    boxes.append(box)

定位标记的顶点连线

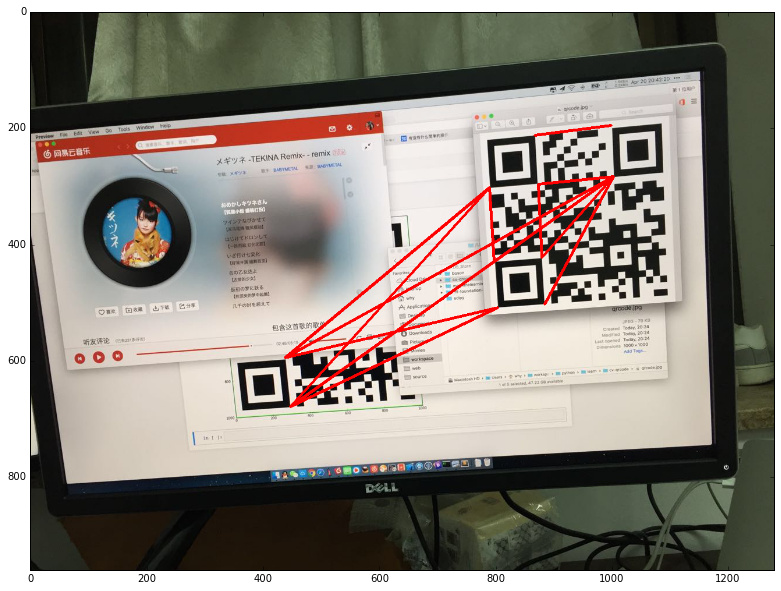
接下来先遍历所有顶点连线，然后从中选择最短的两根，并将它们绘制出来：

def cv_distance(P, Q):
    return int(math.sqrt(pow((P[0] - Q[0]), 2) + pow((P[1] - Q[1]),2)))

def check(a, b):
    # 存储 ab 数组里最短的两点的组合
    s1_ab = ()
    s2_ab = ()
    # 存储 ab 数组里最短的两点的距离，用于比较
    s1 = np.iinfo('i').max
    s2 = s1
    for ai in a:
        for bi in b:
            d = cv_distance(ai, bi)
            if d < s2:
                if d < s1:
                    s1_ab, s2_ab = (ai, bi), s1_ab
                    s1, s2 = d, s1
                else:
                    s2_ab = (ai, bi)
                    s2 = d              
    a1, a2 = s1_ab[0], s2_ab[0]
    b1, b2 = s1_ab[1], s2_ab[1]
    # 将最短的两个线画出来
    cv2.line(draw_img, a1, b1, (0,0,255), 3)
    cv2.line(draw_img, a2, b2, (0,0,255), 3)

for i in range(len(boxes)):
    for j in range(i+1, len(boxes)):
        check(boxes[i], boxes[j])
show(draw_img)

绘制结果如下：

学习笔记：使用 OpenCV 识别 QRCode

获取连线上的像素值

有了端点连线，接下来需要获取连线上的像素值，以便后面判断是否是 Timing Pattern 。

在这之前，为了更方便的判断黑白相间的情况，先对图像进行二值化：

th, bi_img = cv2.threshold(img_gray, 100, 255, cv2.THRESH_BINARY)

接下来是获取连线像素值。由于 OpenCV3 的 Python 库中没有 LineIterator ，只好自己写一个。在《OpenCV 3.0 Python LineIterator》这个问答里找到了可用的直线遍历函数，可以直接使用。

以一条 Timing Pattern 为例：

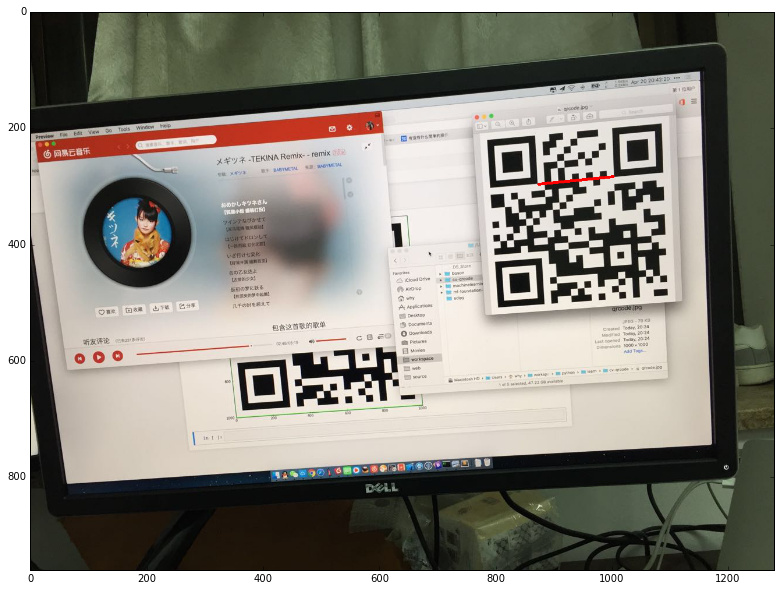
学习笔记：使用 OpenCV 识别 QRCode

打印其像素点看下结果：

[ 255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.
    0.  255.  255.  255.    0.    0.    0.    0.    0.    0.    0.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.  255.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.
    0.    0.    0.  255.  255.  255.  255.  255.  255.  255.  255.  255.
  255.    0.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.]

修正端点位置

照理说， Timing Pattern 的连线，像素值应该是黑白均匀相间才对，为什么是上面的这种一连一大片的结果呢？

仔细看下截图可以发现，由于取的是定位标记的外部包围盒的顶点，所以因为误差会超出定位标记的范围，导致没能正确定位到 Timing Pattern ，而是相邻的 Data 部分的像素点。

为了修正这部分误差，我们可以对端点坐标进行调整。因为 Position Detection Pattern 的大小是固定的，是一个 1-1-3-1-1 的黑白黑白黑相间的正方形，识别 Timing Pattern 的最佳端点应该是最靠里的黑色区域的中心位置，也就是图中的绿色虚线部分：

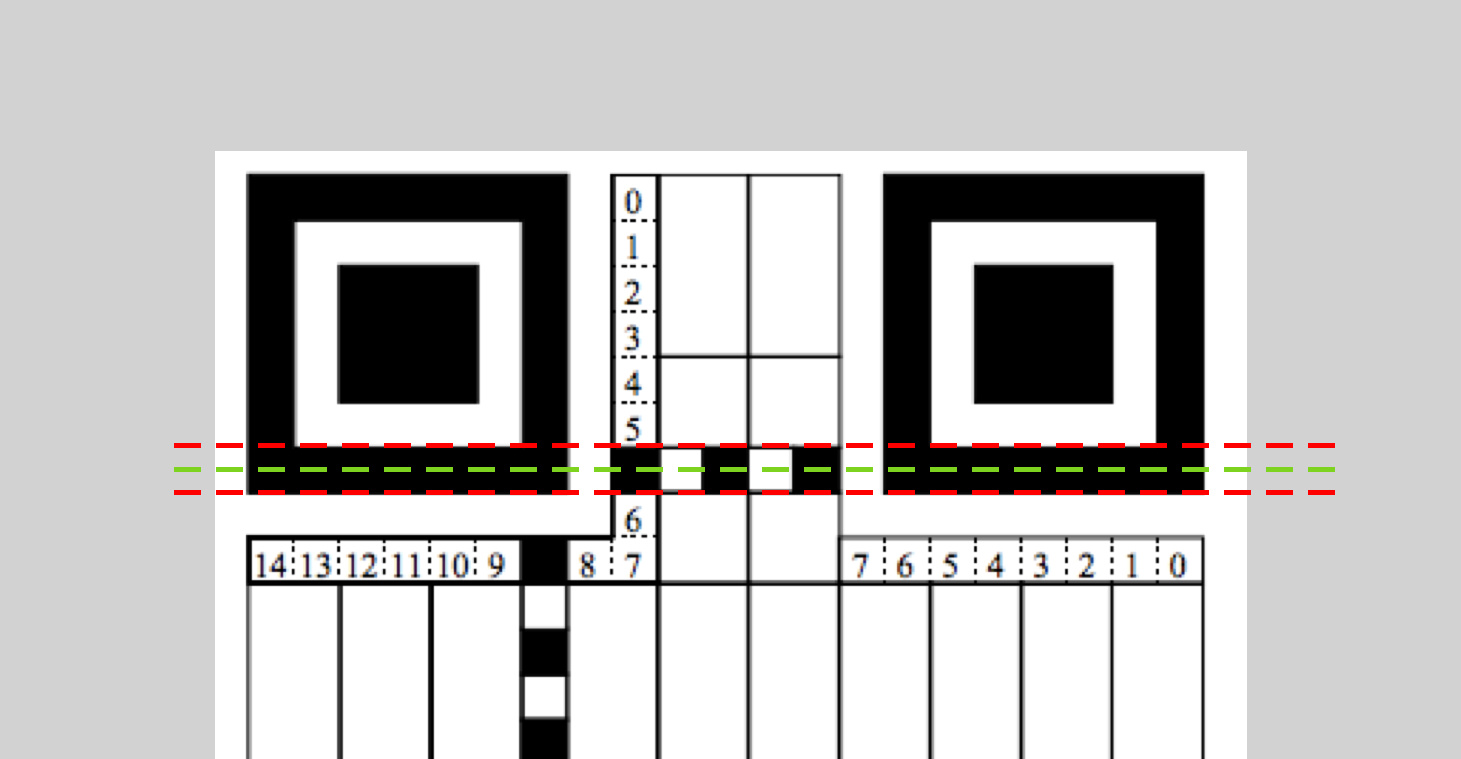
学习笔记：使用 OpenCV 识别 QRCode

所以我们需要对端点坐标进行调整。调整方式是，将一个端点的 x 和 y 值向另一个端点的 x 和 y 值靠近 1/14 个单位距离，代码如下：

a1 = (a1[0] + (a2[0]-a1[0])*1/14, a1[1] + (a2[1]-a1[1])*1/14)
b1 = (b1[0] + (b2[0]-b1[0])*1/14, b1[1] + (b2[1]-b1[1])*1/14)
a2 = (a2[0] + (a1[0]-a2[0])*1/14, a2[1] + (a1[1]-a2[1])*1/14)
b2 = (b2[0] + (b1[0]-b2[0])*1/14, b2[1] + (b1[1]-b2[1])*1/14)

调整之后的像素值就是正确的 Timing Pattern 了：

[ 255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.    0.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.  255.    0.    0.
    0.    0.    0.    0.    0.    0.    0.    0.    0.    0.  255.  255.
  255.  255.  255.  255.  255.  255.  255.  255.  255.]

验证是否是 Timing Pattern

像素序列拿到了，接下来就是判断它是否是 Timing Pattern 了。 Timing Pattern 的特征是黑白均匀相间，所以每段同色区域的计数结果应该相同，而且旋转拉伸平移都不会影响这个特征。

于是，验证方案是：

先除去数组中开头和结尾处连续的白色像素点。
对数组中的元素进行计数，相邻的元素如果值相同则合并到计数结果中。比如 [0,1,1,1,0,0] 的计数结果就是 [1,3,2] 。
计数数组的长度如果小于 5 ，则不是 Timing Pattern 。
计算计数数组的方差，看看分布是否离散，如果方差大于阈值，则不是 Timing Pattern 。

代码如下：


def isTimingPattern(line):
    # 除去开头结尾的白色像素点
    while line[0] != 0:
        line = line[1:]
    while line[-1] != 0:
        line = line[:-1]
    # 计数连续的黑白像素点
    c = []
    count = 1
    l = line[0]
    for p in line[1:]:
        if p == l:
            count = count + 1
        else:
            c.append(count)
            count = 1
        l = p
    c.append(count)
    # 如果黑白间隔太少，直接排除
    if len(c) < 5:
        return False
    # 计算方差，根据离散程度判断是否是 Timing Pattern
    threshold = 5
    return np.var(c) < threshold

对前面的那条连线检测一下，计数数组为：

[11, 12, 11, 12, 11, 12, 11, 13, 11]

方差为 0.47 。其他非 Timing Pattern 的连线方差均大于 10 。

找出错误的定位标记

接下来就是利用前面的结果除去错误的定位标记了，只要两个定位标记的端点连线中能找到 Timing Pattern ，则这两个定位标记有效，把它们存进 set 里：

valid = set()
for i in range(len(boxes)):
    for j in range(i+1, len(boxes)):
        if check(boxes[i], boxes[j]):
            valid.add(i)
            valid.add(j)
print valid

结果是：

set([1, 2, 3])

好了，它们中出了一个叛徒，0、1、2、3 四个定位标记，0是无效的，1、2、3 才是需要识别的 QRCode 的定位标记。

找出二维码

有了定位标记之后，找出二维码就轻而易举了。只要找出三个定位标记轮廓的最小矩形包围盒，那就是二维码的位置了：

contour_all = np.array([])
while len(valid) > 0:
    c = found[valid.pop()]
    for sublist in c:
        for p in sublist:
            contour_all.append(p)

rect = cv2.minAreaRect(contour_ALL)
box = cv2.boxPoints(rect)
box = np.array(box)

draw_img = img.copy()
cv2.polylines(draw_img, np.int32([box]), True, (0, 0, 255), 10)
show(draw_img)