实时大数据流上的频率统计：Lossy Counting Algorithm
大数据交流QQ群，汇聚2万大数据爱好者。 加入，开启你的数据江湖！！
在大数据处理中，或是面试中，经常会遇到这样的问题：
比如，一个社交网站上有上亿的用户主页，而且每天有上十亿的访问量，想实时知道最常被访问的主页有哪些，然后给出一个排名。常用的做法是给每个主页一个计数器，这样需要很大的内存(往往装不下)来保存这些计数器，但极大多数的计数器其实只有一次两次，这是一个非常大的浪费，而且现实资源不允许这么做。
再比如，一个网站有海量的IP访问。为了检测爬虫或是DOS，需要计算一个IP在一个时间单位(比如一分钟，一小时，一天，等)中访问的次数，然后屏蔽或是captcha单位时间内访问次数过多的IPs。由于web server中能用来统计IP访问次数的内存资源有限，不可能存储所有的访问IPs。
还有很多类似的例子，比如，一段时间内的流行商品，一段时间内的人气王，经常被拨打的电话，作弊的账号，等等。
对于这些实时数据流的频率统计问题，有在数学上可能保证错误小于某个要求值的近似算法，Lossy Counting Algorithm 就是 Gurmeet Singh Manku 提出和证明的一个算法。
这些问题都可以统一为以下的问题描述，对于一个数据流，找出所有的频率大于某个值(通常表示为总数的百分比，这里用s表示)的所有元素，进而可以找出top n。
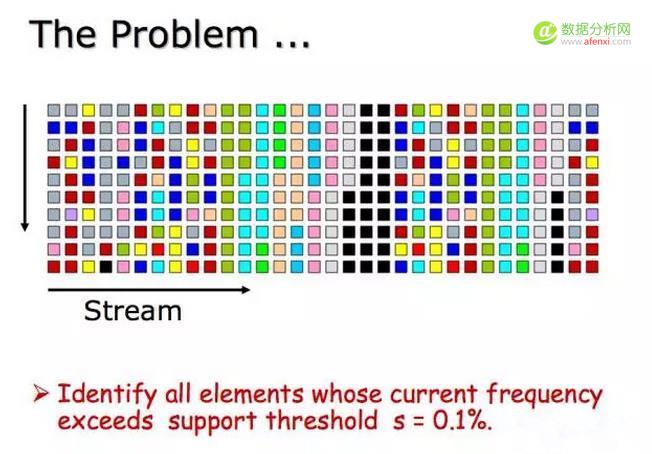
Lossy Couting 算法的第一步是将数据流分成一样大小的很多个窗口(或是片)。窗口的大小和期望的错误率息息相关。之后具体讨论。
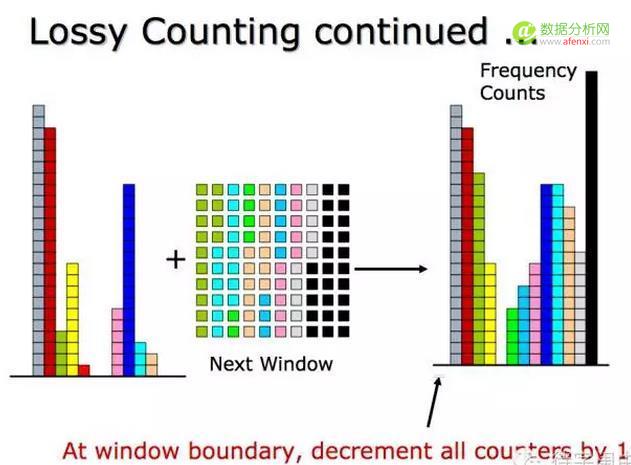
从第一个窗口开始，计算每个元素的频率。注意了，高明之处来了，在窗口结束时，将每个元素的计数减一，然后将哪些计数值为零的元素从内存中删除。这样在保证近似性的同时也限制了内存资源的占用。妙吧!
然后，处理下一个窗口中的元素，同样，在窗口的结束时，将每个元素的计数减一，同时清除那些计数为零的元素。直到所有数据处理完毕，或是实时流数据的检查点到了。最后，将内存中的元素按频率排序，就能得当当前的top n。
很明显，Lossy Counting 算法是个近似算法，但它的错误是可以分析和数学上可以证明它的边界的。如果错误率是e，窗口大小为1/e(哈哈，这样才能保证错误率小)，对于长度为N的流，有N/(1/e)=eN 个窗口，由于每个窗口结束时减一了，那么频率最多被少计数了窗口个数eN。
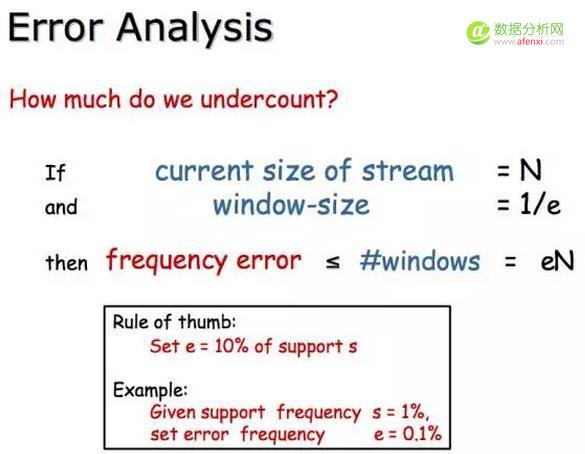
最后留下的元素是频率超过 sN-eN的。近似算法能保证：
- 频率最多被少算eN;
- 没有错误的反例(不应该出来的元素出来了);
- 错误的正例有的真实频率至少是sN-eN。
最后，内存的使用的最坏情况是 1/e log (eN) 个计数器。参考 阅读原文 看证明。
算法提高。具体参考论文《Approximate Frequency Counts over Data Streams》。
对于实时大数据处理，很多情况下，由于资源限制，需要采用近似的算法。对于近似算法，一定要在理论上是可以证明的。Lossy Counting Algorithm 就是经过证明的算法，在实际工作中是可以放心的使用的。
来源：微信公众号 待字闺中
注：数据分析网遵循行业规范，任何转载的稿件都会明确标注作者和来源，若标注有误，请联系主编邮箱：afenxi@afenxi.com
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
