转载

时序分析在生物医学上的应用

几年前作者在学院的环境流行病课程上做了关于时序分析的演讲课程。这个课程的主要基调是：你应该忽略从时序模型、论文或者课本上读到的信息，说这个观点的原因是作者发现一些时序研究的相关文献在做生物医学和人口卫生环境分析方面并不是那么靠谱。

数据预测 VS 数据推断

大部分时序模型的文献都假设你对数据预测感兴趣，比如，典型的时序类型天气预报。作者也不列外，在研究空气污染和死亡率时，没能找到更好的模型来预测死亡率。特别地，如果我们的目标是预测死亡率，我们可能根本不会把空气污染作为变量。因为空气污染天然的和人口死亡率是弱相关性，而像温度和其他季节因素和人口死亡率有极强的关系。

作者现在正在研究的是评估空气污染的水平和死亡率间的关系，并对这种关系做某种推断，增加人口数或者周期性变化。这种分析的挑战在于在这么多的强相关性的变量中评估弱相关性，并调整潜在的混淆变量。

数据预测和推论之间的区别非常重要的原因是，如果你把注意力放在一方面，那将导致你得到不同的模型构建策略。数据预测模型总是让你把各种强相关的因素加入到模型中，并对结果进行解释。如果你试图做数据推断，但你使用了数据预测策略，这时你可能犯两种错误：

你可能因为模型策略不包括某种变量就得出主要的变量（e. g. 空气污染）不重要的结论；
你可能因为混淆变量和结果有弱相关性而忽略一个潜在的重要混淆变量。例如，空气污染研究中潜在的混淆变量可能是其他污染，而这类污染物可能和死亡率弱相关但与你感兴趣的环境污染有强相关性。

随机性 VS 不变性

另外一个时序模型文献讲述的跟作者实践的经历不同在于是聚焦固定效应还是随机效应。常见的时序模型（i. e. 自回归模型（AR），移动平均模型（MA），广义自回归条件异方差模型（GARCH）等）都是聚焦在模型的随机性部分。经常你使用随机性时序模型是因为你没有其他数据。但是在许多生物医学和公共卫生环境方面的实际情况，时序模型应该解释为固定效应模型。

考虑下面的时序例子。在时序的起始点和结束点，值比较低；而在中间区域比较高，呈正弦函数。

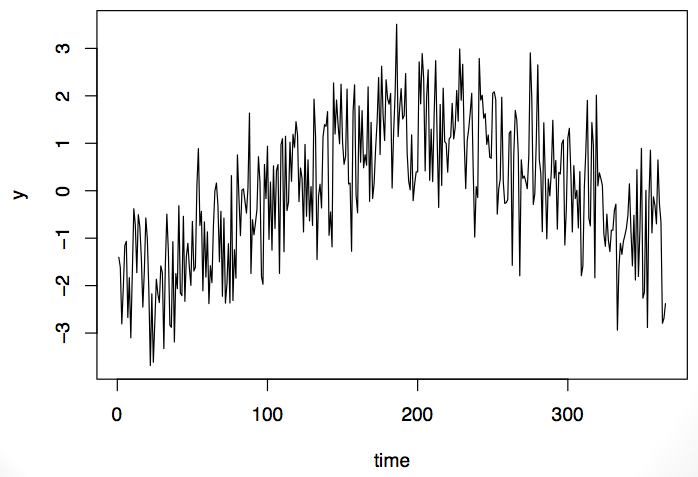
时序分析在生物医学上的应用

这个时序数据可以构建成自回归模型（AR）或者自回归移动平均模型（ARMA）。或者数据展示成季节模型。数据不能告诉你是随机模型或者是你预期的模式。问题在于我们经常只观察时间序列的一个观察值。

现在看看另外一个时序数据。它和第一个时序数据有相同的属性：在时间起始点和结束点观察值较低，中间部分观察值较高。

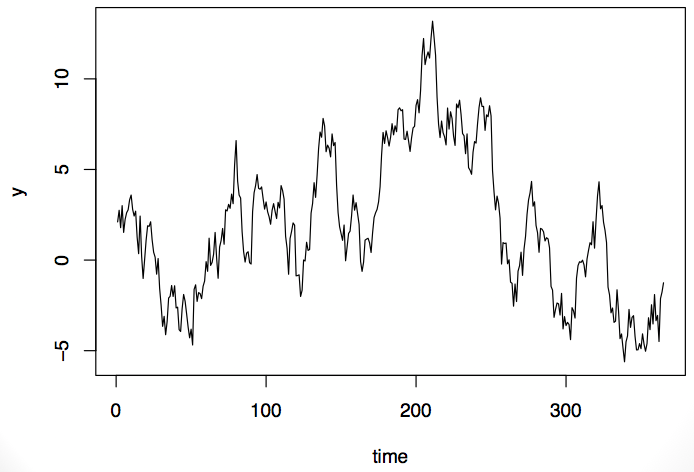
时序分析在生物医学上的应用

那我们应该选择随机效应模型还是固定效应模型？这完全依赖于数据的类型和我们所了解的信息。如果是空气污染数据，我们可能选择一种模型；而如果是股票交易数据，我们可能选择完全不同的模型。

如果都有一个复制的时序数据集，我们能解决是固定模型还是随机模型的问题。例如，作者模拟上面的数据，看看发生了什么。通过画图可以看到两个不同时序数据的复制数据集。

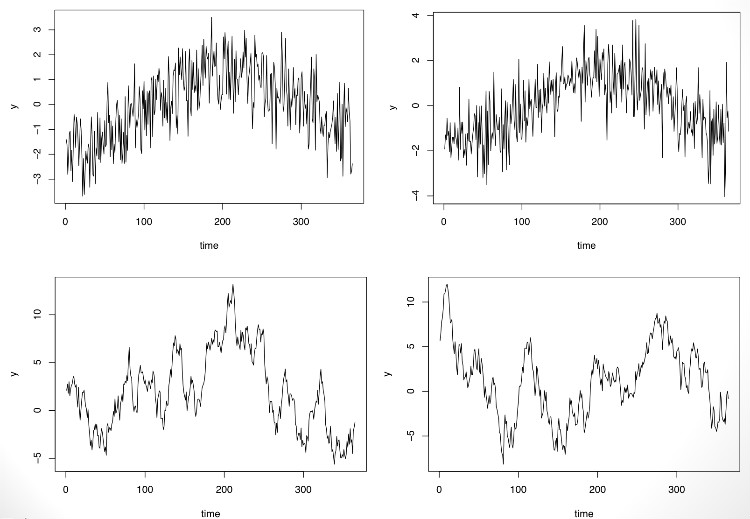
时序分析在生物医学上的应用

很清晰的看出上面一行的时间序列是固定型的季节型模式，而下面一行的时序数据是随机型模型（实际上是用AR模型模拟出来的）。

我经常性的把固定性变量引入到时序数据中：季节模式，天的影响和长期的趋势。更近一步，其他时间协变量可以帮我们预测时序数据集。当更多的固定性因素考虑进去时，残留中的感兴趣的值变小。

怎样建立模型？

接下来的问题：我该如何建立模型？简短回答就是尽可能包含你已知的数据到固定性模型／回归模型，然后看一下残留误差。

下面拿空气污染和死亡率的研究举例子。数据是1987年到2000年美国美国底特律城市总括性死亡率和PM10值。问题是是否每天的PM10的水平变化和每天的人口死亡率有关。我们试图用简单线性回归模型来回答：

Call: lm(formula = death ~ pm10, data = ds)  Residuals:     Min      1Q  Median      3Q     Max  -26.978  -5.559  -0.386   5.109  34.022   Coefficients:              Estimate Std. Error t value Pr(>|t|) (Intercept) 46.978826   0.112284 418.394   <2e-16 pm10         0.004885   0.001936   2.523   0.0117  Residual standard error: 8.03 on 5112 degrees of freedom Multiple R-squared:  0.001244,  Adjusted R-squared:  0.001049  F-statistic: 6.368 on 1 and 5112 DF,  p-value: 0.01165

PM10值与人口死亡率有正相关性，但是我们看下残差的自相关函数：

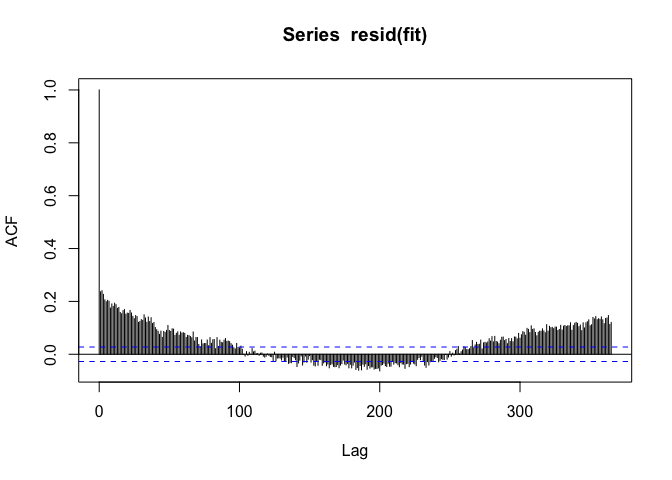
时序分析在生物医学上的应用

如果我们在自相关函数中看到了季节性模式，那意味着在残差中有季节性模式。但是我们用季节指标来调整模型考虑季节因素。

Call: lm(formula = death ~ season + pm10, data = ds)  Residuals:     Min      1Q  Median      3Q     Max  -25.964  -5.087  -0.242   4.907  33.884   Coefficients:              Estimate Std. Error t value    Pr(>|t|) (Intercept) 50.830458   0.215679 235.676     < 2e-16 seasonQ2    -4.864167   0.304838 -15.957     < 2e-16 seasonQ3    -6.764404   0.304346 -22.226     < 2e-16 seasonQ4    -3.712292   0.302859 -12.258     < 2e-16 pm10         0.009478   0.001860   5.097 0.000000358  Residual standard error: 7.649 on 5109 degrees of freedom Multiple R-squared:  0.09411,   Adjusted R-squared:  0.09341  F-statistic: 132.7 on 4 and 5109 DF,  p-value: < 2.2e-16

注意到PM10的系数，当增加了季节因素系数有些增大。

当我们再看下残差图：

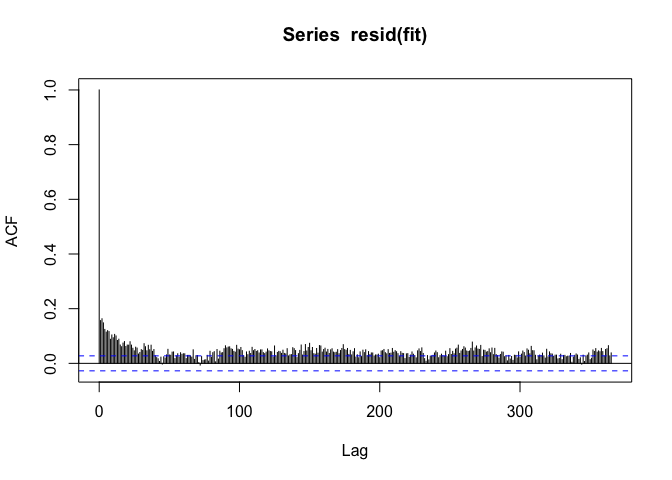
时序分析在生物医学上的应用

季节模式不见了，但同时也可以看到与时间的长度有正的自相关性，这经常会出现在一些时间跨度长的数据中。因为这里仅仅关注PM10和死亡率每天的变化，因此可以去除长期的趋势。作者仅仅引入日期作为一个线性变量。

Call: lm(formula = death ~ season + date + pm10, data = ds)  Residuals:     Min      1Q  Median      3Q     Max  -23.407  -5.073  -0.375   4.718  32.179   Coefficients:                Estimate  Std. Error t value    Pr(>|t|) (Intercept) 60.04317325  0.64858433  92.576     < 2e-16 seasonQ2    -4.76600268  0.29841993 -15.971     < 2e-16 seasonQ3    -6.56826695  0.29815323 -22.030     < 2e-16 seasonQ4    -3.42007191  0.29704909 -11.513     < 2e-16 date        -0.00106785  0.00007108 -15.022     < 2e-16 pm10         0.00933871  0.00182009   5.131 0.000000299  Residual standard error: 7.487 on 5108 degrees of freedom Multiple R-squared:  0.1324,    Adjusted R-squared:  0.1316  F-statistic:   156 on 5 and 5108 DF,  p-value: < 2.2e-16

接下来再看一个自相关函数的列子。

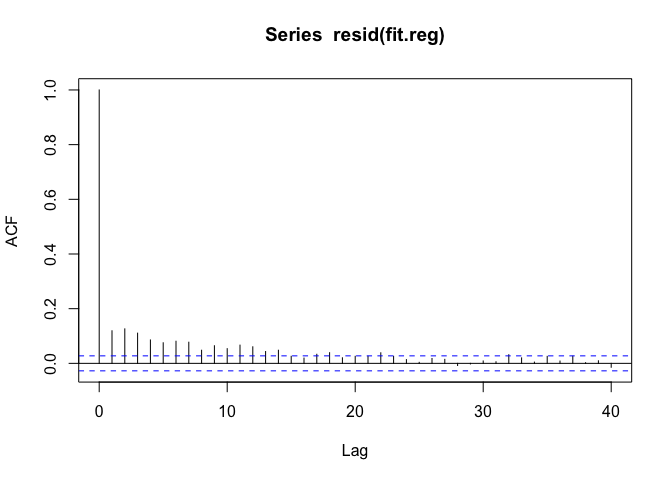
时序分析在生物医学上的应用

自相关函数的轨迹趋近于0，但仍然有短暂的滞后15天的自相关性。

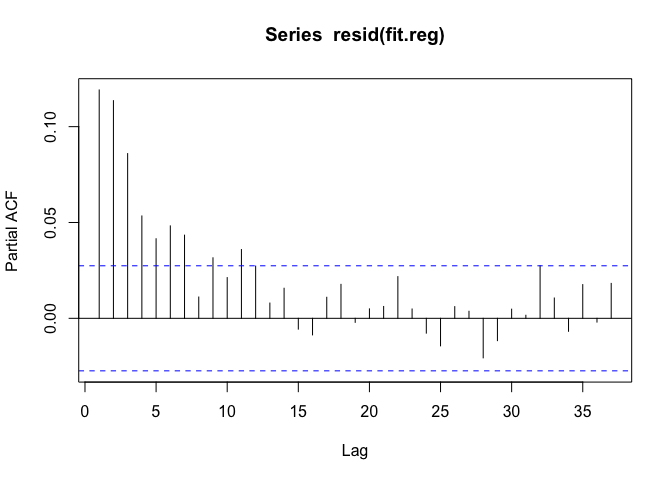
时序分析在生物医学上的应用

现在看下传统的时序模型，这里采用p阶自相关模型。这里的p是什么呢？我们通过偏自相关函数（PACF）获得p。偏自相关函数（PACF）似乎建议用AR(6)或者AR(7)模型。我们采用arima()

Call: arima(x = y, order = c(6, 0, 0), xreg = m, include.mean = FALSE)  Coefficients:          ar1     ar2     ar3     ar4     ar5     ar6  (Intercept)       0.0869  0.0933  0.0733  0.0454  0.0377  0.0489      59.8179 s.e.  0.0140  0.0140  0.0141  0.0141  0.0140  0.0140       1.0300       seasonQ2  seasonQ3  seasonQ4     date    pm10        -4.4635   -6.2778   -3.2878  -0.0011  0.0096 s.e.    0.4569    0.4624    0.4546   0.0001  0.0018  sigma^2 estimated as 53.69:  log likelihood = -17441.84,  aic = 34909.69

可以看到PM10的系数与初始的模型并没有什么变化。在本例子中，使用带残差自相关的AR(6)模型和忽略残差自相关得到的结果没多大区别。下面比较了每个系数的标准残差：

               Naive AR model (Intercept) 0.648584 1.030007 seasonQ2    0.298420 0.456883 seasonQ3    0.298153 0.462371 seasonQ4    0.297049 0.454624 date        0.000071 0.000114 pm10        0.001820 0.001819

pm10的标准差几乎一样，但是其他变量在自回归模型（AR）中的标准差较大。