转载

数组和矩阵 2 - 矩阵

继续是《数据结构算法与应用：C++语言描述》，第四章数组和矩阵的笔记。本小节介绍矩阵的基本概念以及自定义一个类Matrix实现基本的矩阵操作。

矩阵

定义和操作

一个$m/times n$的矩阵(matrix)是一个m行、n列的表，如下图所示，其中m和n是矩阵的维数。
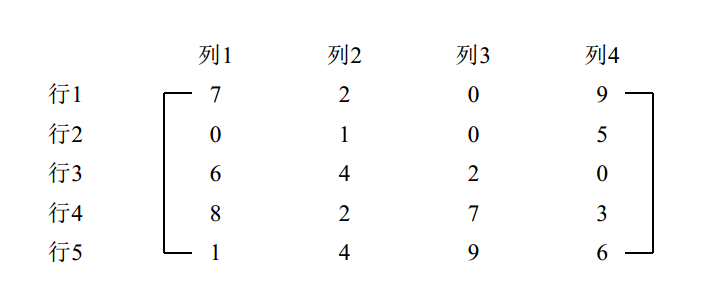
数组和矩阵 2 - 矩阵

对于矩阵来说，最常见的操作就是矩阵转置、矩阵加和矩阵乘。

一个$m/times n$矩阵的转置矩阵是一个$n/times m$的矩阵$M^T$,它与$M$之间存在以下关系：
$$
M^T(i,j) = M(j,i)/quad 1/le i/le n,/; 1/le j/le m
$$

仅当两个矩阵的维数相同时，即具有相同的行数和列数，才可以对两个矩阵求和。两个$m/times n$矩阵$A和B$相加所得到的$m/times n$矩阵$C$如下：
$$
C(i,j) =A(i,j)+B(i,j)/quad 1/le i/le n,/; 1/le j/le m
$$

仅当一个$m/times n$矩阵$A$的列数与另一个$q/times p$矩阵$B$的行数相同，即 n=q ,才可以执行矩阵乘法$A B$。其得到的$m/times p$矩阵$C$满足以下关系：
$$
C(i,j) = /sum_{k=1}^nA(i,k)/ / B(k,j)/quad 1/le i/le m,/; 1/le j/le p
$$

矩阵加的代码实现如下

template<class T> void Add( T **a, T **b, T **c, int rows, int cols) {     // 矩阵 a 和 b 相加得到矩阵 c .     for (int i = 0; i < rows; i++)         for (int j = 0; j < cols; j++)              c[i][j] = a[i][j] + b[i][j]; }

矩阵转置代码实现如下：

template<class T> void Transpose(T **a, int rows) {     // 对矩阵 a[0:rows-1][0:rows-1] 进行转置     for (int i = 0; i < rows; i++)         for (int j = i+1; j < rows; j++)             Swap(a[i][j], a[j][i]); }

矩阵乘法的代码实现如下：

template<class T> void Mult(T **a, T **b, T **c, int m, int n, int p) {     // m x n 矩阵 a 与 n x p 矩阵 b相乘得到c     for (int i = 0; i < m; i++)         for (int j = 0; j < p; j++) {             T sum = 0;             for (int k = 0; k < n; k++)                 sum += a[i][k] * b[k][j];             c[i][j] = sum;         } }

类Matrix

这里自定义一个类Matrix来实现矩阵的功能，在该类中，使用 () 来指定每个元素，并且各行和各列的索引值都是从1开始的。
其类定义如下：

#ifndef MATRIX_H_ #define MATRIX_H_ #include<iostream> using std::ostream; template<class T> class Matrix{ private:     int rows, cols;     // 元素数组     T *element;  public:     Matrix(int r = 0, int c = 0);     // 复制构造函数     Matrix(const Matrix<T>& m);     ~Matrix(){ delete[] element; }     int Rows() const{ return rows; }     int Columns() const{ return cols; }     T& operator()(int i, int j)const;     Matrix<T>& operator=(const Matrix<T>& m);     Matrix<T> operator+() const;     Matrix<T> operator+(const Matrix<T>& m)const;     Matrix<T> operator-() const;     Matrix<T> operator-(const Matrix<T>& m)const;     Matrix<T> operator*(const Matrix<T>& m)const;     Matrix<T>& operator+=(const T& m);     void Output(ostream& out) const; }; #endif

构造函数，复制构造函数以及赋值运算符的代码如下：

template<class T> Matrix<T>::Matrix(int r, int c){     if (r < 0 || c < 0)         throw BadInitializers();     if ((!r || !c) && (r || c))         throw BadInitializers();     rows = r;     cols = c;     element = new T[r*c]; }  template<class T> Matrix<T>::Matrix(const Matrix<T>& m){     // 复制构造函数     rows = m.rows;     cols = m.cols;     element = new T[rows*cols];     int size = rows * cols;     for (int i = 0; i < size; i++)         element[i] = m.element[i]; }  template<class T> Matrix<T>& Matrix<T>::operator=(const Matrix<T>& m){     // 重载赋值运算符=     if (*this != &m){         rows = m.rows;         cols = m.cols;         delete[] element;         element = new T[rows*cols];         int size = rows * cols;         for (int i = 0; i < size; i++)             element[i] = m.element[i];     }     return *this; }

为了重载矩阵下标操作法(),使用了C++的函数操作符()，与数组的下标操作法[]不同的是，该操作符可以带任意数量的参数。对于一个矩阵来说，需要两个整数参数。如下所示

template<class T> T& Matrix<T>::operator()(int i, int j)const{     // 返回一个指向元素(i,j)的引用     if (i<1 || i>rows || j<1 || j>cols)         throw OutOfBounds();     return element[(i - 1)*cols + j - 1]; }

二元减法的代码如下，矩阵加法操作符，一元减法操作符，增值操作符和输出操作符的代码都比较类似。

template<class T> Matrix<T> Matrix<T>::operator-(const Matrix<T>& m)const{     if (rows != m.rows || cols != m.cols)         throw SizeMismatch();     Matrix<T> w(rows, cols);     for (int i = 0; i < rows * cols; i++){         w.element[i] = element[i] - m.element[i];     }     return w; }

矩阵乘法实现如下所示

template<class T> Matrix<T> Matrix<T>::operator*(const Matrix<T>& m)const{     // 矩阵乘法 返回w = (*this) * m     if (cols != m.rows)         throw SizeMismatch();     Matrix<T> w(rows, m.cols);     int ct = 0, cm = 0, cw = 0;     for (int i = 1; i <= rows; i++){         // 计算出结果的第i行         for (int j = 1; j <= m.cols; j++){             // 计算w(i,j)的第一项             T sum = element[ct] * m.element[cm];             // 累加其余项             for (int k = 2; k <= cols; k++){                 // 指向*this第i行的下一个元素                 ct++;                 // 指向m的第j列的下一项                 cm += m.cols;                 sum += element[ct] * m.element[cm];             }             // 保存w(i,j)             w.element[cw++] = sum;             // 重新调整至行首和下一列             ct -= cols - 1;             cm = j;         }         // 重新调整至下一行的行首和第一列         ct += cols;         cm = 0;     }     return w; }

更完整的例子可以查看我的 Github