转载

数组和矩阵 3 - 特殊矩阵

继续是《数据结构算法与应用：C++语言描述》，第四章数组和矩阵的笔记。本小节介绍几种特殊矩阵的内容。

定义和应用

方阵是指具有相同行数和列数的矩阵。

一些常用的特殊方阵如下：

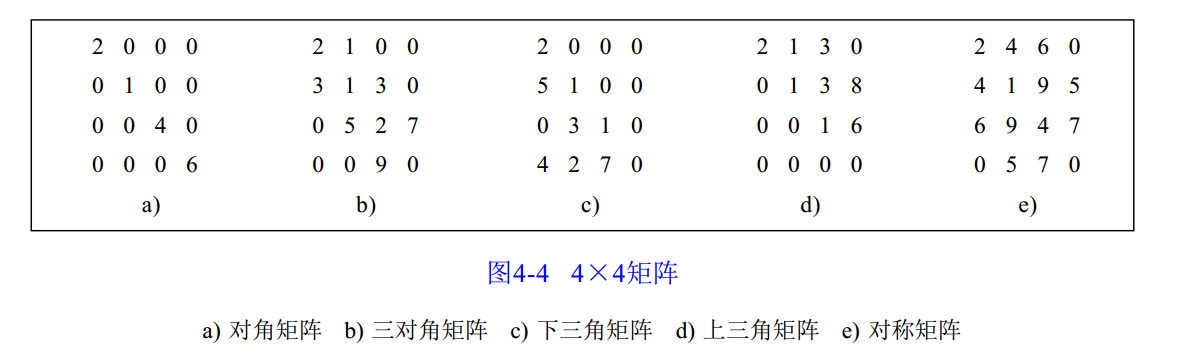
对角矩阵 $M$是一个对角矩阵，当前仅当$i /neq j$时，有$M(i,j)=0$。如下图a所示
三对角矩阵 $M$是一个三对角矩阵，当前仅当$|i-j| /gt 1$时有$M(i,j)=0$。如下图b所示
下三角矩阵 $M$是一个下三角矩阵，当前仅当$i/lt j$时有$M(i,j)=0$。如下图c所示
上三角矩阵 $M$是一个上三角矩阵，当前仅当$i/gt j$时有$M(i,j)=0$。如下图d所示
对称矩阵 $M$是一个对称矩阵，当前仅当对于所有的$i 和 j$有$M(i,j)=M(j,i)$。如下图e所示

数组和矩阵 3 - 特殊矩阵

对角矩阵

可以采用 T d[n][n] 这样的二维数组来描述一个元素类型为T的$n /times n$对角矩阵D。
使用数组元素 d[i-1][j-1] 来表示矩阵元素 D(i,j) ，这种描述形式所需要的存储空间为$n^2 * sizeof(T)$。

由于一个对角矩阵最大包含n个非0元素，所以可以采用 T d[n] 一维数组来描述对角矩阵。其中使用 d[i-1] 表示矩阵元素 D(i,i) ，而根据对角矩阵的定义，所有未在一维数组中出现的矩阵元素均为0.

这里使用如下自定义类 DiagonalMatrix 来实现这种描述。

#ifndef DIAGONALMATRIX_H_ #define DIAGONALMATRIX_H_  template<class T> class DiagonalMatrix{ private:     // 矩阵维数     int n;     // 存储对角元素的一维数组     T *d;        public:     DiagonalMatrix(int size = 10): n(size){         d = new T[n];     }     ~DiagonalMatrix(){ delete[] d; }     DiagonalMatrix<T>& Store(const T& x, int i, int j);     T Retrieve(int i, int j)const; };  template<class T> DiagonalMatrix<T>& DiagonalMatrix<T>::Store(const T&x, int i, int j){     // 将x存为D(i,j)     if (i<1 || j<1 || i>n || j>n)         throw OutOfBounds();     if (i != j && x != 0)         // 必须满足对角矩阵的条件：i != j 时，x必须为0         throw MustBeZero();     if (i == j)         d[i - 1] = x;     return *this; }  template<class T> T DiagonalMatrix<T>::Retrieve(int i, int j)const{     if (i<1 || j<1 || i>n || j>n)         throw OutOfBounds();     if (i == j)         return d[i - 1];     return 0; } #endif

对于存储和搜索操作，提供了两个不同的函数，而不是使用重载操作符()来完成。此外在存储一个值时，必须保证不会在非对角线位置放置一个非0值；而搜索一个值时，没有必要检查对角线以外的值，因此有必要对这两种情形区别对待。两个函数的复杂性均为$/theta(1)$。

三对角矩阵

在一个$n /times n$三对角矩阵T中，非0元素排列在如下的三条对角线上：

主对角线—— i=j
主对角线之下的对角线(称低对角线)—— i=j+1
主对角线之上的对角线(称高对角线)—— i=j-1

这三条对角线上的元素总数为 3n-2 ，故可以使用一个拥有3n-2个位置的一维数组来描述T。考察上述图b中所示的$4/times 4$三对角矩阵，三条对角线上总共10个元素。如果将其逐行映射到一维数组t中，则有 t[0:9]=[2,1,3,1,3,5,2,7,9,0] ;如果逐列映射到t中，则有 t=[2,3,1,1,5,3,2,9,7,0] ;如果按照对角线的次序，从最下面的对角线开始进行映射，则有 t=[3,5,9,2,1,2,0,1,3,7] 。所以这里有三种不同的方式来进行T到t的映射。
下面的程序定义了类 TridiagonalMatrix ,其中采用了对角线映射方式。

template<class T> class TridiagonalMatrix{ private:     int n;     T *t; public:     TridiagonalMatrix(int size = 10) : n(size){         t = new T[3 * n - 2];     }     ~TridiagonalMatrix(){delete[] t;}     TridiagonalMatrix<T>& Store(const T& x, int i, int j);     T Retrieve(int i, int j)const; };  template<class T> TridiagonalMatrix<T>& TridiagonalMatrix<T>::Store(const T& x, int i, int j){     // 把x存为T(i,j)     if (i<1 || j<1 || i>n || j>n)         throw OutOfBounds();     switch (i-j){         case 1:             // 低对角线             t[i - 2] = x;             break;         case 0:             // 主对角线             t[n - 2 + i] = x;             break;         case -1:             // 高对角线             t[2 * n - 2 + i] = x;             break;         default:             if (x != 0)                 throw MustBeZero();     }     return *this; }  template<class T> T TridiagonalMatrix<T>::Retrieve(int i, int j)const{     if (i<1 || j<1 || i>n || j>n)         throw OutOfBounds();     switch (i - j){     case 1:         // 低对角线         return t[i - 2];     case 0:         // 主对角线         return t[n - 2 + i];     case -1:         // 高对角线         return t[2 * n - 2 + i];     default:         return 0;     } }

这里首先是从最下面的对角线开始，也就是低对角线，那么T(i,j)对应的一维数组是t[i-2]，接着轮到主对角线的时候，只需要用i加上低对角线的元素总数，即n-2个，也就是对应数组t[n-2+i]，因为i是依次从1，按行逐渐增加；最后对于高对角线，也是同样的计算方法。

三角矩阵

在三角矩阵中，无论是上三角还是下三角矩阵，非0元素总数均为$/frac{n(n+1)}{2}$。

两种三角矩阵都可以用一个大小为$/frac{n(n+1)}{2}$的一维数组进行描述。考虑把一个下三角矩阵映射到一个一维数组$l$，可以采用按行和按列两种不同的方式进行映射。如果按行映射，上图c中$4/times 4$下三角矩阵可以得到$l[0:9] = (2,5,1,0,3,1,4,2,7,0)$;若按列的方式，得到$l[0:9] =(2,5,0,4,1,3,2,1,7,0)$。

所以对于下三角矩阵中的一个元素$L(i,j)$，如果$i/lt j$,则$L(i,j)=0$;如果$i/le j$，则$L(i,j)$位于非0元素区域，且其对应的一维数组是 t[$/frac{i(i-1)}{2}+j-1$] ，其映射规则是先统计前i-1行的非0元素数量然后加上当前元素所在第i行的所在列数j-1。下面给出自定义类 LowerMatrix 实现下三角矩阵,并且是按行来映射。

template<class T> class LowerMatrix{ private:     // 矩阵维数     int n;     // 存储对角元素的一维数组     T *t; public:     LowerMatrix(int size = 10) : n(size){         t = new T[n*(n+1)/2];     }     ~LowerMatrix(){ delete[] t; }     LowerMatrix<T>& Store(const T& x, int i, int j);     T Retrieve(int i, int j)const; };  template<class T> LowerMatrix<T>& LowerMatrix<T>::Store(const T&x, int i, int j){     // 将x存为D(i,j)     if (i<1 || j<1 || i>n || j>n)         throw OutOfBounds();     // 当前仅当 i >= j时，(i,j)位于下三角     if (i >= j)         t[i*(i - 1) / 2 + j - 1] = x;     else if (x != 0)         throw MustBeZero();     return *this; }  template<class T> T LowerMatrix<T>::Retrieve(int i, int j)const{     if (i<1 || j<1 || i>n || j>n)         throw OutOfBounds();     if (i >= j)         return t[i*(i - 1) / 2 + j - 1];     else         return 0; }

上三角矩阵的实现方式也是相同的，只需要改变判断条件，将$i /ge j$变成$i /le j$即可。

对称矩阵

一个$n/times n$的对称矩阵可以用一个大小为$/frac{n(n+1)}{2}$的一维数组来描述，可参考三角矩阵的存储模式来存储矩阵的上三角或下三角，即可以根据已经存储的元素来推算出未存储的元素。即如果存储下三角的元素，当需要给出在上三角的元素，只需要将行和列对调，再来搜索即可得到需要的元素值，这样做可以更节省空间。