转载

DirectX 3D学习笔记02——3D数学基础

3D数学是一门和计算几何相关的学科，广泛应用于使用计算机来模拟3D世界的领域，比如图形学、仿真、游戏等等。本文主要介绍了游戏开发中常用的3D数学基础知识以及D3DX中提供的相关接口。

本文部分图片来自于 http://learnopengl.com

3D坐标系

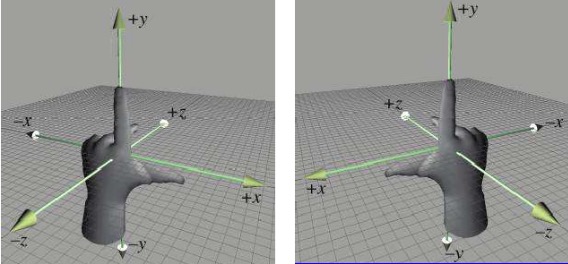
3D坐标系分为左手坐标系和右手坐标系，如下图所示，两个坐标系之间无法通过旋转进行转换。其中OpenGL使用的是右手坐标系，而Direct 3D使用的是左手坐标系， 本文使用左手坐标系进行介绍。

相机模型

为了将一个3D空间中的物体在2D屏幕上显示，需要进行一系列转换，在转换过程中会用到几个矩阵，分别为模型矩阵(Model)、视图矩阵(View)、投影矩阵(Projection)，下图展示了整个转换流程。

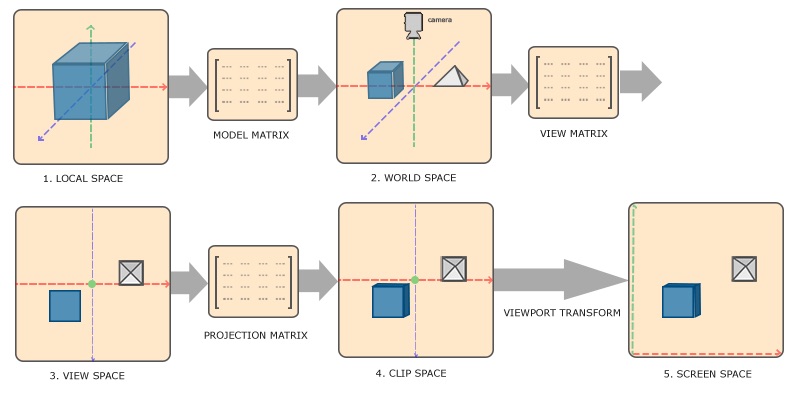
DirectX 3D学习笔记02——3D数学基础

简化后的流程如下图所示。

首先我们使用局部空间定义模型坐标，这样在构建模型时就无需考虑位置、大小等问题。
[模型变换] 通过模型矩阵(Model)，我们将模型从局部空间放到世界空间，模型变换包括平移、缩放、旋转。
[视图变换] 我们观察3D世界的位置可以虚拟成一个摄像机，该摄像机可以在3D世界的任一位置，为了简化运算，我们将摄像机变换到世界空间中的原点，并朝向z轴正方向。为了保证摄像机的视场恒定，需要通过视图矩阵(View)将模型坐标从世界空间转换到观察空间中。
[投影变换] 将模型放到观察坐标系后，会通过投影矩阵(Projection)进行投影变换，将3D场景投影到2D平面上。实现投影的方式包括正交投影和透视投影，在后面会进行介绍。投影变换后只有坐标在-1到1之间的点在摄像机的可见范围内。
[视口变换] 可视范围内的模型会通过视口变换显示在窗口中。

如果对以上过程难以理解的话，可以类比我们使用摄像机拍摄一个物体的过程：

将物体放置到某个地方(模型变换)
将摄像机放到某个位置，并对准某个方向，这时以摄像机为世界中心(视图变换)
设置相机焦距，调整缩放比例(投影变换)
拍摄照片到胶卷中(视口变换)

齐次坐标

在数学中，一个N维向量与N*N的矩阵相乘，可以得到一个新的N维向量。

空间中的坐标是三维的笛卡尔坐标，将三维的笛卡尔坐标转换成四维的 齐次坐标 后，就可以使用矩阵乘法完成坐标的旋转、平移、缩放和投影等操作。

为什么要使用四维的齐次坐标？

三维矩阵乘法无法实现平移操作
可用于透视投影，第四个分量越大，说明该点越远。(x,y,z,w)最后投影到平面上的点为(x/w,y/w,z/w)

以上这两点在后面的内容都会有所说明。在D3DX中，可以通过D3DXMATRIX操作齐次矩阵。对于四维向量，如果表示一个点，则第四维为1，如果表示一个向量，则第四维为0。

模型变换

模型变换包括平移、缩放及旋转三类变换。

平移矩阵

平移并不是一种线性变换(平移一个向量是无效的操作)，所以只使用三维是无法构造平移矩阵的。举例来说，原点(0,0,0)乘以任何矩阵得到的结果都只会是(0,0,0)。

将(x,y,z)平移到(x+Δx,y+Δy,z+Δz)，构造的矩阵如下。

$/begin{bmatrix} x & y & z & 1 /end{bmatrix} /begin{bmatrix} 1 & 0 & 0 & 0 // 0 & 1 & 0 & 0 // 0 & 0 & 1 & 0 // /Delta x & /Delta y & /Delta z & 1 /end{bmatrix} = /begin{bmatrix} x+/Delta x & y+/Delta y & z+/Delta z & 1 /end{bmatrix}$ [ x y z 1 ] ⎣ ⎢ ⎢ ⎡ 1 0 0 Δ x 0 1 0 Δ y 0 0 1 Δ z 0 0 0 1 ⎦ ⎥ ⎥ ⎤ = [ x + Δ x y + Δ y z + Δ z 1 ]

在D3DX中，使用D3DXMatrixTranslation创建一个平移矩阵。

D3DXMATRIX *D3DXMatrixTranslation(
    D3DXMATRIX *pOut,
    FLOAT x, FLOAT y, FLOAT z
);

缩放矩阵

让(x,y,z)沿着x,y,z轴分别放大qx、qy、qz倍，构造的矩阵如下。

$/begin{bmatrix} x & y & z & 1 /end{bmatrix} /begin{bmatrix} q_{x} & 0 & 0 & 0 // 0 & q_{y} & 0 & 0 // 0 & 0 & q_{z} & 0 // 0 & 0 & 0 & 1 /end{bmatrix} = /begin{bmatrix} q_{x}x & q_{x}y & q_{x}z & 1 /end{bmatrix}$ [ x y z 1 ] ⎣ ⎢ ⎢ ⎡ q x 0 0 0 0 q y 0 0 0 0 q z 0 0 0 0 1 ⎦ ⎥ ⎥ ⎤ = [ q x x q x y q x z 1 ]

在D3DX中，使用D3DXMatrixScaling创建一个缩放矩阵。

D3DXMATRIX *D3DXMatrixScaling(
    D3DXMATRIX *pOut,
    FLOAT sx, FLOAT sy, FLOAT sz
);

旋转矩阵

在3D空间中旋转需要一个角度和一个轴，而所有的旋转都由绕X，Y，Z轴分别旋转组合而成。

以绕X轴旋转θ为例，构造的旋转矩阵如下。

$/begin{bmatrix} x & y & z & 1 /end{bmatrix} /begin{bmatrix} 1 & 0 & 0 & 0 // 0 & /cos /theta & /sin /theta & 0 // 0 & -/sin /theta & /cos /theta & 0 // 0 & 0 & 0 & 1 /end{bmatrix} = /begin{bmatrix} x & y/cos /theta-z/sin /theta & y/sin /theta+z/cos /theta & 1 /end{bmatrix}$ [ x y z 1 ] ⎣ ⎢ ⎢ ⎡ 1 0 0 0 0 cos θ − sin θ 0 0 sin θ cos θ 0 0 0 0 1 ⎦ ⎥ ⎥ ⎤ = [ x y cos θ − z sin θ y sin θ + z cos θ 1 ]

在D3DX中，使用D3DXMatrixRotationX创建一个绕X轴旋转的矩阵。

D3DXMATRIX *D3DXMatrixRotationX(
    D3DXMATRIX *pOut,
    FLOAT Angle
);

类似的，还有D3DXMatrixRotationY，D3DXMatrixRotationZ两个函数。

此外，D3DX还提供了一个绕任意轴旋转的函数D3DXMatrixRotationAxis，该函数中需要指定旋转轴。

D3DXMATRIX* D3DXMatrixRotationAxis(
    D3DXMATRIX  *pOut,
    const D3DXVECTOR3 *pV,
    FLOAT       Angle
);

多个旋转在组合的时候，会产生一个严重的问题—— 万向节死锁 ，使得坐标无法正常旋转，这里不讨论细节，可以自行Google。解决此问题的最好方案是使用 四元数 。

组合

在实际工程中，我们将一个模型坐标从局部空间转换到世界空间，需要进行选择、平移、缩放等多步操作。由于矩阵乘法是满足结合律的，我们可以将这几种操作的矩阵先乘起来，形成所谓的模型矩阵，最后再将局部空间坐标乘以模型矩阵，即可得到其在世界空间中的坐标。

这种组合后一次性变换对性能的提高也是颇有意义的。对于一个庞大的向量集合，我们不再需要对每个向量都依次进行平移、旋转、缩放操作，而是乘一个模型矩阵就搞定了。

此外，这几个操作的顺序问题也是必须要注意的。先旋转(缩放)再平移、还是先平移再旋转(缩放)，得到的结果是完全不一样的，需要根据实际需求谨慎选择顺序。

D3DX提供了如下两个函数分别用于点和向量的变换。其中D3DXVec3TransformCoord用于点变换，并假定第四个分量为1，D3DXVec3TransformNormal用于向量变换，并假定第四个分量为0。

D3DXVECTOR3 *D3DXVec3TransformCoord(
    D3DXVECTOR3* pOut;
    CONST D3DXVECTOR3* pV,  // pointer to transform
    CONST D3DXMATRIX* pM    
);
D3DXVECTOR3 *D3DXVec3TransformNormal(
    D3DXVECTOR3* pOut;
    CONST D3DXVECTOR3* pV,  // vector to transform
    CONST D3DXMATRIX* pM    
);

D3DX可以通过IDirectDevice9::SetTransform方法来设定当前渲染用到的模型矩阵。

SetTransform(D3DTS_WORLD, pM);

视图变换

视图变换就是将世界空间变换成以摄像机为中心的视图空间。

我们使用postion,up,right,look四个变量来定义摄像机，其中postion是摄像机的位置，其他三个分别表示摄像机的上向量、右向量与观察向量。

设我们最终得到的视图变换矩阵为V，那我们希望通过这个矩阵将postion变换到原点，right变换为x轴，up变换为y轴，look变换为z轴，即该变换需满足以下条件

$/left/{/begin{matrix} p=(p_{x},p_{y},p_{z}) & pV=(0,0,0) // r=(r_{x},r_{y},r_{z}) & rV=(1,0,0) // u=(u_{x},u_{y},u_{z}) & uV=(0,1,0) // d=(d_{x},d_{y},d_{z}) & dV=(0,0,1) /end{matrix}/right.$ ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ p = ( p x , p y , p z ) r = ( r x , r y , r z ) u = ( u x , u y , u z ) d = ( d x , d y , d z ) p V = ( 0 , 0 , 0 ) r V = ( 1 , 0 , 0 ) u V = ( 0 , 1 , 0 ) d V = ( 0 , 0 , 1 )

据此可以推出矩阵V

$V = /begin{bmatrix} r_{x} & u_{x} & d_{x} & 0 // r_{y} & u_{y} & d_{y} & 0 // r_{z} & u_{z} & d_{z} & 0 // -pr & -pu & -pz & 1 /end{bmatrix}$ V = ⎣ ⎢ ⎢ ⎡ r x r y r z − p r u x u y u z − p u d x d y d z − p z 0 0 0 1 ⎦ ⎥ ⎥ ⎤

D3DX中可以使用D3DXMatrixLookAtLH方法获取视图矩阵

D3DXMATRIX *D3DXMatrixLookAtLH(
    D3DXMATRIX *pOut,
    CONST D3DXMATRIX *pEye, CONST D3DXMATRIX *pAt, CONST D3DXMATRIX *pUp
)；

获得视图矩阵后，通过IDirectDevice9::SetTransform方法来设定当前渲染用到的视图矩阵。

SetTransform(D3DTS_VIEW, pM);

投影变换

投影变换是将三维空间投影到二维平面上的过程。投影变换分为透视投影和正交投影，透视投影类似于人眼的观察视角，会产生近大远小的视觉效果，而正交投影不会，也因此主要用于一些工程建模软件中。

D3DX以近平面作为投影平面，投影过后，会将投影平面内的x坐标转化到范围[-w,w],y坐标范围[-w,w],z坐标范围[0,w]，投影完成后，实际坐标(x’,y’,z’)=(x/w, y/w, z/w)，D3DX会裁剪掉范围外的投影。

同样的模型在透视投影和正交投影下的渲染效果。

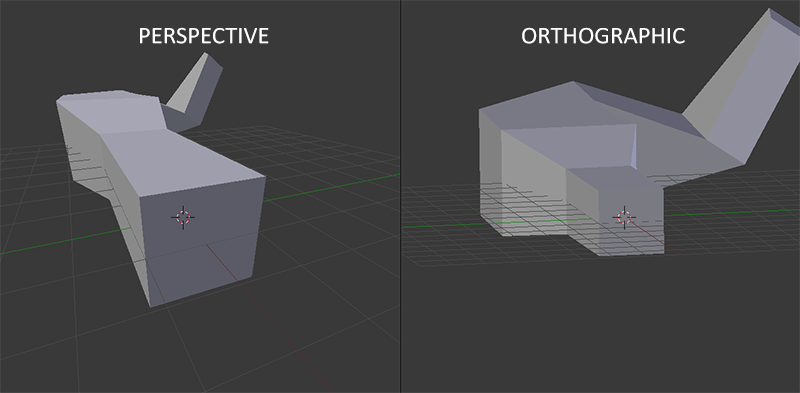
获得视图矩阵后，通过IDirectDevice9::SetTransform方法来设定当前渲染用到的投影矩阵。

SetTransform(D3DTS_PROJECTION, pM);

透视投影

透视投影实际上是一个视锥体，根据视角角度、近平面以及远平面可以构造一个四棱台，只有这个四棱台范围内的模型才是可见的。

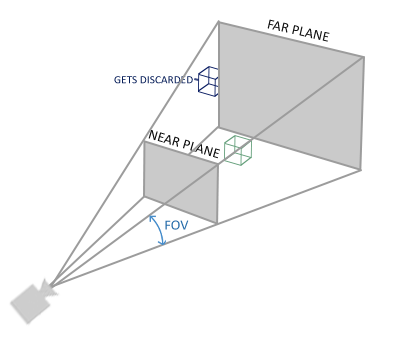
DirectX 3D学习笔记02——3D数学基础

假设窗口的高度是height，宽度是width，近平面到摄像机的距离为n，远平面到摄像机的距离为f，可以得到透视投影变换矩阵如下，具体的推导过程可以自行google。

$/begin{bmatrix} /frac{n}{width/2} & 0 & 0 & 0 // 0 & /frac{n}{height/2} & 0 & 0 // 0 & 0 & /frac{f}{f-n} & 1 // 0 & 0 & /frac{nf}{n-f} & 0 /end{bmatrix}$ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ w i d t h / 2 n 0 0 0 0 h e i g h t / 2 n 0 0 0 0 f − n f n − f n f 0 0 1 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤

D3DX中可以使用以下两个方法获取透视投影变换矩阵。其中第二个函数中fovy代表纵向的视角角度，aspect代表宽高比，稍微修改上面的变换矩阵就可以得到等价的变换矩阵(根据cot(fovy/2)=2n/height，aspect=width/height进行推导)。

D3DXMATRIX* D3DXMatrixPerspectiveLH(
  D3DXMATRIX *pOut,
  FLOAT w, FLOAT h, FLOAT zn, FLOAT zf
)
D3DXMATRIX* D3DXMatrixPerspectiveFovLH(
  D3DXMATRIX *pOut,
  FLOAT fovy, FLOAT Aspect, FLOAT zn, FLOAT zf
)

正交投影

正交投影相对透视投影要简单一些，其可视范围是一个长方体。

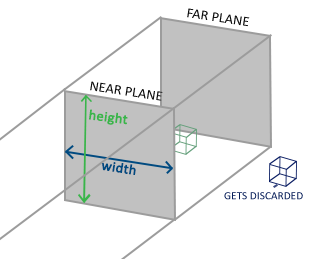
DirectX 3D学习笔记02——3D数学基础

正交投影变换矩阵的推导也比较简单，就是一个缩放然后平移的过程。

$/begin{bmatrix} /frac{2}{width} & 0 & 0 & 0 // 0 & /frac{2}{height} & 0 & 0 // 0 & 0 & /frac{1}{f-n} & 0 // 0 & 0 & /frac{n}{n-f} & 1 /end{bmatrix}$ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ w i d t h 2 0 0 0 0 h e i g h t 2 0 0 0 0 f − n 1 n − f n 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤

D3DX中可以使用以下方法获取正交投影变换矩阵。

D3DXMATRIX* D3DXMatrixOrthoRH(
  D3DXMATRIX *pOut,
  FLOAT w, FLOAT h, FLOAT zn, FLOAT zf
);

视口变换

投影变换后的坐标满足x范围[-1,1]，y范围[-1,1]，z范围[0,1]，w=1，视口变换是将窗口从投影窗口转换到屏幕的一个矩形区域中。其中左上角(-1, 1, 0, 1)映射到(X, Y, MinZ, 1)，右上角(1, -1, 0, 1)映射到(X+Width, Y+Height, MinZ, 1),

视口变换矩阵如下，其中涉及到的参数含义如下，(x,y)表示矩形区域左上角的坐标，width和height分别表示宽和高，[MinZ,MaxZ]指定深度缓存的范围，一般设置为[0,1]即可。

$/begin{bmatrix} /frac{width}{2} & 0 & 0 & 0 // 0 & -/frac{height}{2} & 0 & 0 // 0 & 0 & MaxZ-MinZ & 0 // x+/frac{width}{2} & y+/frac{width}{2} & MinZ & 1 /end{bmatrix}$ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 2 w i d t h 0 0 x + 2 w i d t h 0 − 2 h e i g h t 0 y + 2 w i d t h 0 0 M a x Z − M i n Z M i n Z 0 0 0 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤

D3DX使用IDirectDevice9::SetViewport来设置视口，设置后D3DX将自动完成视口变换。

typedf struct _D3DVIEWPORT9 {
    DWORD x, DWORD y, DWORD width, DWORD height, DWORD MinZ, DWORD MaxZ
} D3DVIEWPORT9;

D3DVIEWPORT9 vp = { 0, 0, 800, 200, 0, 1 };
m_pDevice->SetViewport(&vp);