基于社区发现算法和图分析Neo4j解读《权利的游戏》上篇
几个月前,数学家 Andrew Beveridge和Jie Shan在数学杂志上发表《权利的网络》,主要分析畅销小说《冰与火之歌》第三部《冰雨的风暴》中人物关系,其已经拍成电视剧《权利的游戏》系列。他们在论文中介绍了如何通过文本分析和实体提取构建人物关系的网络。紧接着,使用社交网络分析算法对人物关系网络分析找出最重要的角色;应用社区发现算法来找到人物聚类。
其中的分析和可视化是用Gephi做的,Gephi是非常流行的图分析工具。但作者觉得使用Neo4j来实现更有趣。
导入原始数据到Neoj
原始数据可从网络上下载,格式如下:
Source,Target,Weight
Aemon,Grenn,5
Aemon,Samwell,31
Aerys,Jaime,18
...
上面是人物关系的之邻接表以及关系权重。作者使用简单的数据模型:(:Character {name})-[:INTERACTS]->(:Character {name})。带有标签Character的节点代表小说中的角色,用单向关系类型INTERACTS代表小说中的角色有过接触。节点属性会存储角色的名字name,两角色间接触的次数作为关系的属性:权重(weight)。
首先创建节点c,并做唯一限制性约束,c.name唯一,保证schema的完整性:
CREATE CONSTRAINT ON (c:Character) ASSERT c.name IS UNIQUE;
一旦约束创建即相应的创建索引,这将有助于通过角色的名字查询的性能。作者使用Neo4j的Cypher(Cypher是一种声明式图查询语言,能表达高效查询和更新图数据库)LOAD CSV语句导入数据:
LOAD CSV WITH HEADERS FROM "https://www.macalester.edu/~abeverid/data/stormofswords.csv" AS row
MERGE (src:Character {name: row.Source})
MERGE (tgt:Character {name: row.Target})
MERGE (src)-[r:INTERACTS]->(tgt)
SET r.weight = toInt(row.Weight)
这样得到一个简单的数据模型:
CALL apoc.meta.graph()
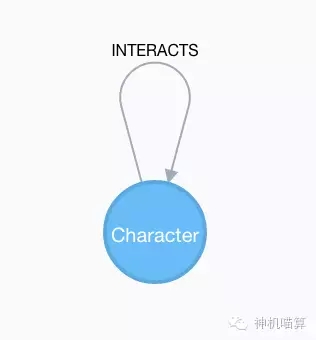
图1 :《权利的游戏》模型的图。Character角色节点由INTERACTS关系联结
我们能可视化整个图形,但是这并不能给我们很多信息,比如哪些是最重要的人物,以及他们相互接触的信息:
MATCH p=(:Character)-[:INTERACTS]-(:Character)
RETURN p
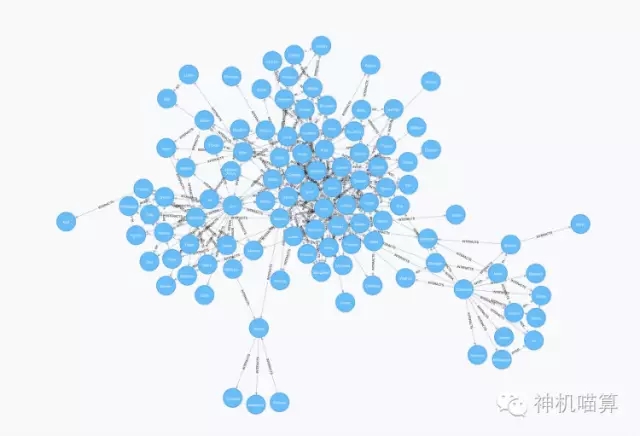
图2
人物网络分析
作者使用Neo4j的图查询语言Cypher来做《权利的游戏》图分析,应用到了网络分析的一些工具,具体见《网络,人群和市场:关于高度连接的世界》。
人物数量
万事以简单开始。先看看上图上由有多少人物:
MATCH (c:Character) RETURN count(c)
╒════════╕
│count(c)│
╞════════╡
│107 │
└────────┘
概要统计
统计每个角色接触的其它角色的数目:
MATCH (c:Character)-[:INTERACTS]->()
WITH c, count(*) AS num
RETURN min(num) AS min, max(num) AS max, avg(num) AS avg_characters, stdev(num) AS stdev
╒═══╤═══╤═════════════════╤═════════════════╕
│min│max│avg_characters │stdev │
╞═══╪═══╪═════════════════╪═════════════════╡
│1 │24 │4.957746478873241│6.227672391875085│
└───┴───┴─────────────────┴─────────────────┘
图(网络)的直径
网络的直径或者测底线或者最长最短路径:
// Find maximum diameter of network
// maximum shortest path between two nodes
MATCH (a:Character), (b:Character) WHERE id(a) > id(b)
MATCH p=shortestPath((a)-[:INTERACTS*]-(b))
RETURN length(p) AS len, extract(x IN nodes(p) | x.name) AS path
ORDER BY len DESC LIMIT 4
╒═══╤════════════════════════════════════════════════════════════╕
│len│path │
╞═══╪════════════════════════════════════════════════════════════╡
│6 │[Illyrio, Belwas, Daenerys, Robert, Tywin, Oberyn, Amory] │
├───┼────────────────────────────────────────────────────────────┤
│6 │[Illyrio, Belwas, Daenerys, Robert, Sansa, Bran, Jojen] │
├───┼────────────────────────────────────────────────────────────┤
│6 │[Illyrio, Belwas, Daenerys, Robert, Stannis, Davos, Shireen]│
├───┼────────────────────────────────────────────────────────────┤
│6 │[Illyrio, Belwas, Daenerys, Robert, Sansa, Bran, Luwin] │
└───┴────────────────────────────────────────────────────────────┘
我们能看到网络中有许多长度为6的路径。
最短路径
作者使用Cypher 的shortestPath函数找到图中任意两个角色之间的最短路径。让我们找出凯特琳·史塔克(Catelyn Stark )和卓戈·卡奥(Kahl Drogo)之间的最短路径:
// Shortest path from Catelyn Stark to Khal Drogo
MATCH (catelyn:Character {name: "Catelyn"}), (drogo:Character {name: "Drogo"})
MATCH p=shortestPath((catelyn)-[INTERACTS*]-(drogo))
RETURN p
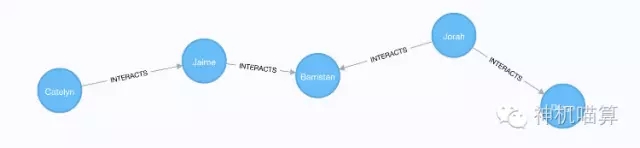
图3
所有最短路径
联结凯特琳·史塔克(Catelyn Stark )和卓戈·卡奥(Kahl Drogo)之间的最短路径可能还有其它路径,我们可以使用Cypher的allShortestPaths函数来查找:
// All shortest paths from Catelyn Stark to Khal Drogo
MATCH (catelyn:Character {name: "Catelyn"}), (drogo:Character {name: "Drogo"})
MATCH p=allShortestPaths((catelyn)-[INTERACTS*]-(drogo))
RETURN p

图4
关键节点
在网络中,如果一个节点位于其它两个节点所有的最短路径上,即称为关键节点。下面我们找出网络中所有的关键节点:
// Find all pivotal nodes in network
MATCH (a:Character), (b:Character)
MATCH p=allShortestPaths((a)-[:INTERACTS*]-(b)) WITH collect(p) AS paths, a, b
MATCH (c:Character) WHERE all(x IN paths WHERE c IN nodes(x)) AND NOT c IN [a,b]
RETURN a.name, b.name, c.name AS PivotalNode SKIP 490 LIMIT 10
╒═══════╤═══════╤═══════════╕
│a.name │b.name │PivotalNode│
╞═══════╪═══════╪═══════════╡
│Aegon │Thoros │Daenerys │
├───────┼───────┼───────────┤
│Aegon │Thoros │Robert │
├───────┼───────┼───────────┤
│Drogo │Ramsay │Robb │
├───────┼───────┼───────────┤
│Styr │Daario │Daenerys │
├───────┼───────┼───────────┤
│Styr │Daario │Jon │
├───────┼───────┼───────────┤
│Styr │Daario │Robert │
├───────┼───────┼───────────┤
│Qhorin │Podrick│Jon │
├───────┼───────┼───────────┤
│Qhorin │Podrick│Sansa │
├───────┼───────┼───────────┤
│Orell │Theon │Jon │
├───────┼───────┼───────────┤
│Illyrio│Bronn │Belwas │
└───────┴───────┴───────────┘
从结果表格中我们可以看出有趣的结果:罗柏·史塔克(Robb)是卓戈·卡奥(Drogo)和拉姆塞·波顿(Ramsay)的关键节点。这意味着,所有联结卓戈·卡奥(Drogo)和拉姆塞·波顿(Ramsay)的最短路径都要经过罗柏·史塔克(Robb)。我们可以通过可视化卓戈·卡奥(Drogo)和拉姆塞·波顿(Ramsay)之间的所有最短路径来验证:
MATCH (a:Character {name: "Drogo"}), (b:Character {name: "Ramsay"})
MATCH p=allShortestPaths((a)-[:INTERACTS*]-(b))
RETURN p
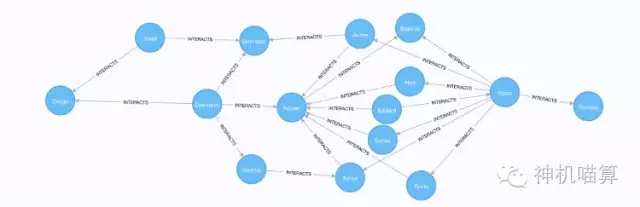
图5
未完待续,更多精彩内容请见下篇文章《基于社区发现算法和图分析Neo4j解读<权利的游戏>下篇》。
参考:
[1]: https://www.macalester.edu/~abeverid/thrones.html
[2]: https://www.macalester.edu/~abeverid/data/stormofswords.csv
[3]: https://www.cs.cornell.edu/home/kleinber/networks-book/
[4]: http://www.lyonwj.com/2016/06/26/graph-of-thrones-neo4j-social-network-analysis/
欢迎加入本站公开兴趣群
软件开发技术群
兴趣范围包括:Java,C/C++,Python,PHP,Ruby,shell等各种语言开发经验交流,各种框架使用,外包项目机会,学习、培训、跳槽等交流
QQ群:26931708
Hadoop源代码研究群
兴趣范围包括:Hadoop源代码解读,改进,优化,分布式系统场景定制,与Hadoop有关的各种开源项目,总之就是玩转Hadoop
QQ群:288410967










![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

