转载

自然语言处理之LDA II-Variational EM实现

上一篇自然语言处理之LDA 使用Gibbs Sampling实现了LDA，本文使用Variational EM实现LDA。

LDA的概率图模型

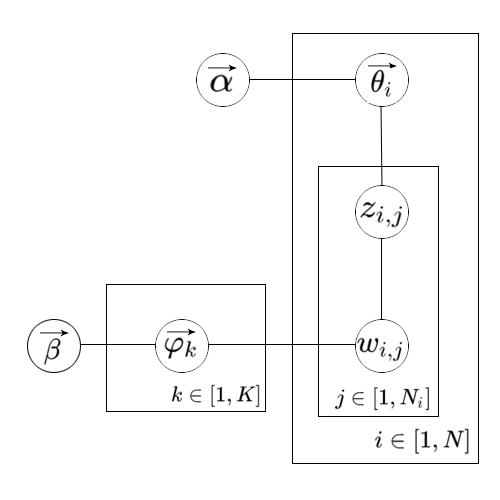
自然语言处理之LDA II-Variational EM实现
符号解释如下：

符号	描述
$N$	文档总数
$N_i$	第i篇文档单词数
$K$	topic总数
$M$	词表长度
$/vec{/alpha}$	document-topic分布的超参数，是一个K维向量
$/vec{/beta}$	topic-word分布的超参数，是一个M维向量
$/vec{/theta_i}$	$p(z{/vert}d=i)$组成的K维向量，其中$z/in[1,K]$
$/vec{/varphi_k}$	$p(w{/vert}z=k)$组成的M维向量，其中$w/in[1,M]$
$z_{i,j}$	第i篇文档的第j个单词的topic编号
$w_{i,j}$	第i篇文档的第j个单词在词表中的编号

文档生成过程

LDA认为数据的生成过程如下图。在具体的实现中，会省略掉某些不重要的过程。比如文档长度$N_i$服从泊松分布的过程，在Gibbs Sampling以及本文Variational EM两种实现中都省略了。
此外，在本文Variational EM的实现中还将省略 ${/varphi_k}$ 的 $/beta$ 先验。
自然语言处理之LDA II-Variational EM实现
那么先回忆一下，在PLSA的实现中使用到了EM算法，在随机的为模型的参数赋值之后就可以在E-Step计算出隐变量的后验概率，从而可以在M-Step优化模型参数，并不断迭代。
因此我们此时也应该尝试推出隐变量的后验概率的计算公式。
根据图模型，可以得到对于一篇文档来说隐变量的后验概率为：
$$
p(/vec{/theta}, /vec{z}|/vec{w},/vec{/alpha},/vec{/varphi})=/frac{p(/vec{/theta}, /vec{z},/vec{w}|/vec{/alpha},/vec{/varphi})}{p(/vec{w}|/vec{/alpha},/vec{/varphi})}
$$
其中分母部分通过引入模型参数可以表示为：
$$
/begin {aligned}
p(/vec{w}|/vec{/alpha},/vec{/varphi}) &={/int}p(/vec{/theta}|/vec{/alpha})(/prod^{N_i}_{n=1}/sum^{K}_{k=1}p(z_n=k|/vec{/theta})p(w_n|z_n=k))d/vec{/theta} //
&={/int}p(/vec{/theta}|/vec{/alpha})(/prod^{N_i}_{n=1}/sum^{K}_{k=1}/prod^M_{j=1}(/theta_k/varphi_{kj})^{w_n^{j}})d/vec{/theta}
/end {aligned}
$$
这里出现了一个新的符号 $w_n^{j}$, 若该篇文档的第 $n$ 个词在词表中的编号为 $j$,则 $w_n^{j}=1$，否则$w_n^{j}=0$。
可以看到 $/theta$ 和 $/varphi$ 以乘积的形式结合在了隐变量的求和之中，因此无法直接根据上式计算出隐变量的后验概率。
因此我们在E-Step使用变分推断(Variational Inference)得到隐变量后验概率的近似值。
在介绍变分推断之前，先介绍一下在变分推断中要用到的Dirichlet分布的一些性质。

Dirichlet distribution

这里介绍Dirichlet分布的形式以及期望的计算公式。若 $/theta{/sim}Dirichlet(/alpha)$,则有：

$$
/begin {aligned}
p(/theta|/alpha) &=/frac{/Gamma(/sum^{K}_{i=1}/alpha_i)}{/sum^{K}_{i=1}/Gamma(/alpha_i)}/prod^{K}_{i=1}{/theta_i}^{/alpha_i-1} //
&=exp((/sum^{K}_{i=1}(/alpha_i-1)log/theta_i)+log/Gamma(/sum^{K}_{i=1}/alpha_i)-/sum^{K}_{i=1}log/Gamma(/alpha_i))
/end {aligned}
$$

第二行将dirichlet分布化为了指数分布族的一般形式，可以得到:
sufficient statistics : $log/theta_i$
log normalizer : $/sum^{K}_{i=1}log/Gamma(/alpha_i)-log/Gamma(/sum^{K}_{i=1}/alpha_i)$
因此可以计算 $log/theta_i$的期望是：

$$
/begin {aligned}
E(log/theta_i) &=(/sum^{K}_{i=1}log/Gamma(/alpha_i)-log/Gamma(/sum^{K}_{i=1}/alpha_i))’ //
&=/psi(/alpha_i)-/psi(/sum^{K}_{j=1}/alpha_j)
/end {aligned}
$$

这里的 $/Gamma$表示gamma函数; $/psi$ 表示digamma函数，是log Gamma函数的一阶导函数。

Variational Inference

变分推断的基本思想

变分推断要做的就是用分布q来近似隐变量的后验概率的分布。定义变分推断图模型如下。
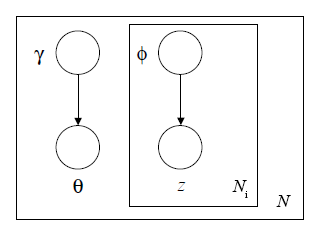
自然语言处理之LDA II-Variational EM实现

根据图模型，可以得到对于隐变量的变分分布：
$$
q(/theta,z|/gamma,/phi)=q(/theta|/gamma)/prod^{N_i}_{n=1}q(z_n|/phi_n)
$$
那么如何来衡量这两个分布的差异性呢？我们使用KL散度（Kullback–Leibler divergence）,KL散度始终大于等于0，当且仅当两个分布相同时KL散度等于0。
我们的目标是找到参数 $/gamma$ 和 $/phi$ 使得KL散度越小越好。
即求解如下的优化问题：
$$
(/gamma^{/ast},/phi^{/ast})={arg}min_{/gamma,/phi}KL(q(/theta,z|/gamma,/phi)||p(/theta, z|w,/alpha,/varphi))
$$

那么我们来计算KL散度。
$$
/begin {aligned}
KL(q(/theta,z|/gamma,/phi)||p(/theta, z|w,/alpha,/varphi)) &=E_q(log/frac{q(/theta,z|/gamma,/phi)}{p(/theta, z|w,/alpha,/varphi)}) //
&=E_q[log(q(/theta,z|/gamma,/phi))]-E_q[log(p(/theta, z |w,/alpha,/varphi))] //
&=E_q[log(q(/theta,z|/gamma,/phi))]-E_q[log(p(/theta, z,w |/alpha,/varphi))]+log(p(w)) //
&=-(E_q[log(p(/theta, z,w |/alpha,/varphi))]-E_q[log(q(/theta,z|/gamma,/phi))])+log(p(w)) //
&=-/mathcal{L}(/gamma,/phi;/alpha,/varphi)+log(p(w))
/end {aligned}
$$
在上式中，令 $/mathcal{L}(/gamma,/phi;/alpha,/varphi)=E_q[log(p(/theta, z,w |/alpha,/varphi))]-E_q[log(q(/theta,z|/gamma,/phi))]$, 称为ELBO（Evidence Lower BOund）。
称其为ELBO是因为 $log(p(w))=/mathcal{L}(/gamma,/phi;/alpha,/varphi)+KL(q(/theta,z|/gamma,/phi)||p(/theta, z|w,/alpha,/varphi))/geq/mathcal{L}(/gamma,/phi;/alpha,/varphi)$。
根据上面的等式，$log(p(w))$是一个定值，因此要使 $KL(q(/theta,z|/gamma,/phi)||p(/theta, z|w,/alpha,/varphi))$最小，只要使得 $/mathcal{L}(/gamma,/phi;/alpha,/varphi)$最大即可。
之所以优化ELBO最大，是因为我们不知道隐变量的后验分布，无法直接优化KL散度最小。
下面计算ELBO。

推导$/mathcal{L}(/gamma,/phi;/alpha,/varphi)$

$$
/begin {aligned}
/mathcal{L}(/gamma,/phi;/alpha,/varphi)&=E_q[log(p(/theta, z,w |/alpha,/varphi))]-E_q[log(q(/theta,z|/gamma,/phi))] //
&=E_q[log(p(/theta|/alpha))]+E_q[log(p(z|/theta))]+E_q[log(p(w|z,/varphi))]-E_q[log(q(/theta|/gamma))]-E_q[log(q(z|/phi))]
/end {aligned}
$$
下面分别推导这5项。

$E_q[log(p(/theta|/alpha))]$

$$
E_q[log(p(/theta|/alpha))]=/sum^{K}_{i=1}(/alpha_i-1)E_q[log/theta_i]+log/Gamma(/sum^{K}_{i=1}/alpha_i)-/sum^{K}_{i=1}log/Gamma(/alpha_i)
$$

$/theta$ is generated from $Dir(/theta|/gamma)$, 因此有$E_q[log/theta_i]=/psi(/gamma_i)-/psi(/sum^{K}_{j=1}/gamma_j)$, 因此：

$$
E_q[log(p(/theta|/alpha))]=/sum^{K}_{i=1}(/alpha_i-1)(/psi(/gamma_i)-/psi(/sum^{K}_{j=1}/gamma_j))+log/Gamma(/sum^{K}_{i=1}/alpha_i)-/sum^{K}_{i=1}log/Gamma(/alpha_i)
$$

$E_q[log(p(z|/theta))]$

$$
/begin {aligned}
E_q[log(p(z|/theta))]&=E_q[/sum^{N_d}_{n=1}/sum^{K}_{i=1}z_{ni}log/theta_i] //
&=/sum^{N_d}_{n=1}/sum^{K}_{i=1}E_q[z_{ni}]E_q[log/theta_i] //
&=/sum^{N_d}_{n=1}/sum^{K}_{i=1}/phi_{ni}(/psi(/gamma_i)-/psi(/sum^{K}_{j=1}/gamma_j))
/end {aligned}
$$
$/theta$ is generated from $Dir(/theta|/gamma)$ and $z$ is generated from $Mult(z|/phi)$。$N_d$表示第d个文档的单词总数。

$E_q[log(p(w|z,/varphi))]$

$$
/begin {aligned}
E_q[log(p(w|z,/varphi))]&=E_q[/sum^{N_d}_{n=1}/sum^{K}_{i=1}/sum^{M}_{j=1}z_{ni}w^{j}_{n}log/varphi_{ij}] //
&=/sum^{N_d}_{n=1}/sum^{K}_{i=1}/sum^{M}_{j=1}E_q[z_{ni}]w^{j}_{n}log/varphi_{ij} //
&=/sum^{N_d}_{n=1}/sum^{K}_{i=1}/sum^{M}_{j=1}/phi_{ni}w^{j}_{n}log/varphi_{ij}
/end {aligned}
$$

$E_q[log(q(/theta|/gamma))]$

$$
/begin {aligned}
E_q[log(q(/theta|/gamma))]&=/sum^{K}_{i=1}(/gamma_i-1)E_q[log/theta_i]+log/Gamma(/sum^{K}_{i=1}/gamma_i)-/sum^{K}_{i=1}log/Gamma(/gamma_i) //
&= /sum^{K}_{i=1}(/gamma_i-1)(/psi(/gamma_i)-/psi(/sum^{K}_{j=1}/gamma_j))+log/Gamma(/sum^{K}_{i=1}/gamma_i)-/sum^{K}_{i=1}log/Gamma(/gamma_i)
/end {aligned}
$$

$E_q[log(q(z|/phi))]$

$$
/begin {aligned}
E_q[log(q(z|/phi))]&=E_q[/sum^{N_d}_{n=1}/sum^{K}_{i=1}z_{ni}log/phi_{ni}] //
&=/sum^{N_d}_{n=1}/sum^{K}_{i=1}E_q[z_{ni}]log/phi_{ni} //
&=/sum^{N_d}_{n=1}/sum^{K}_{i=1}/phi_{ni}log/phi_{ni}
/end {aligned}
$$

最终可以得到：
$$
/begin {aligned}
/mathcal{L}(/gamma,/phi;/alpha,/varphi)&=/sum^{K}_{i=1}(/alpha_i-1)(/psi(/gamma_i)-/psi(/sum^{K}_{j=1}/gamma_j))+log/Gamma(/sum^{K}_{i=1}/alpha_i)-/sum^{K}_{i=1}log/Gamma(/alpha_i) //
&+/sum^{N_d}_{n=1}/sum^{K}_{i=1}/phi_{ni}(/psi(/gamma_i)-/psi(/sum^{K}_{j=1}/gamma_j)) //
&+/sum^{N_d}_{n=1}/sum^{K}_{i=1}/sum^{M}_{j=1}/phi_{ni}w^{j}_{n}log/varphi_{ij} //
&-(/sum^{K}_{i=1}(/gamma_i-1)(/psi(/gamma_i)-/psi(/sum^{K}_{j=1}/gamma_j))+log/Gamma(/sum^{K}_{i=1}/gamma_i)-/sum^{K}_{i=1}log/Gamma(/gamma_i)) //
&-(/sum^{N_d}_{n=1}/sum^{K}_{i=1}/phi_{ni}log/phi_{ni})
/end {aligned}
$$

变分参数的更新

$/phi$的更新

$/mathcal{L}(/gamma,/phi;/alpha,/varphi)$式中包含$/phi$参数的项表示为：

$$
/mathcal{L}_{/phi_{ni}}=/phi_{ni}(/psi(/gamma_i)-/psi(/sum^{K}_{j=1}/gamma_j))+/phi_{ni}log/varphi_{iw}-/phi_{ni}log/phi_{ni}+/lambda(/sum^{K}_{j=1}/phi_{ni}-1)
$$
其中，$/phi_{ni}log/varphi_{iw}$项中的$w$表示该篇文档第$n$个词在词表中的编号，是对前面推导出的式子的等价变换。最后一项是为了使用拉格朗日乘子法加的一项，注意该项结果为0，目的是便于求导。

求导，得到：
$$
/frac{/partial{/mathcal{L}}}{/partial{/phi_{ni}}}=(/psi(/gamma_i)-/psi(/sum^{K}_{j=1}/gamma_j))+log/varphi_{iw}-log/phi_{ni}-1+/lambda
$$
令导数为0，得到：
$$
/phi_{ni}/propto/varphi_{iw}exp(/psi(/gamma_i)-/psi(/sum^{K}_{j=1}/gamma_j))
$$
因此可以根据该式计算$/phi$，再归一化即可。

$/gamma$的更新

$/mathcal{L}(/gamma,/phi;/alpha,/varphi)$式中包含$/gamma$参数的项表示为：

$$
/mathcal{L}_{/gamma}=/sum^{K}_{i=1}(/psi(/gamma_i)-/psi(/sum^{K}_{j=1}/gamma_j))(/alpha_i+/sum^{N_d}_{n=1}/phi_{ni}-/gamma_{i})-log/Gamma(/sum^{K}_{i=1}/gamma_i)+/sum^{K}_{i=1}log/Gamma(/gamma_i))
$$

求导，得到：
$$
/frac{/partial{/mathcal{L}}}{/partial{/gamma_{i}}}=/psi{‘}(/gamma_i)(/alpha_i+/sum^{N_d}_{n=1}/phi_{ni}-/gamma_i)-/psi{‘’}(/sum^{K}_{j=1}/gamma_{j})/sum^{K}_{j=1}(/alpha_j+/sum^{N_d}_{n=1}/phi_{nj}-/gamma_j)
$$

令导数为0，得到：
$$
/gamma_i=/alpha_i+/sum^{N_d}_{n=1}/phi_{ni}
$$
这样就得到了$/gamma$的更新公式。

变分推断算法流程

LDA的变分推断算法流程如下图，用来计算变分参数$/phi$和$/gamma$。
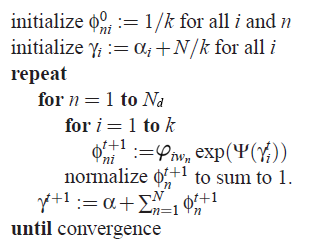
自然语言处理之LDA II-Variational EM实现

Variational EM

变分EM算法流程

1.初始化充分统计量，根据充分统计量初始化模型参数$/alpha$和$/varphi$。
2.迭代执行以下步骤直到收敛：
(E-Step)对于每一篇文档，执行上述的变分推断算法，计算优化的变分参数$/phi$和$/gamma$，并根据变分参数计算充分统计量。
(M-Step)根据充分统计量，更新模型参数$/alpha$和$/varphi$。

M-Step

E-Step如何计算变分参数前面的变分推断算法已经介绍了，这里解释一下M-Step如何更新模型参数$/alpha$和$/varphi$。同样是通过最大化ELBO来实现的。

$/varphi$的更新

$/mathcal{L}(/gamma,/phi;/alpha,/varphi)$式中包含$/varphi$参数的项表示为（对所有文档的值做了求和）,同样使用了拉格朗日乘子法：

$$
/mathcal{L}_{/varphi}=/sum^{N}_{d=1}/sum^{N_d}_{n=1}/sum^{K}_{i=1}/sum^{M}_{j=1}/phi_{dni}w^{j}_{dn}log/varphi_{ij}+/sum^{K}_{i=1}/lambda_{i}(/sum^{M}_{j=1}/varphi_{ij}-1)
$$
该式对 $/varphi_{ij}$求导并令导数等于0，可以得到:
$$
/varphi_{ij}/propto/sum^{N}_{d=1}/sum^{N_d}_{n=1}/phi_{dni}w^{j}_{dn}
$$

$/alpha$的更新

$/mathcal{L}(/gamma,/phi;/alpha,/varphi)$式中包含$/alpha$参数的项表示为:
$$
/mathcal{L}_{/alpha}=/sum^{N}_{d=1}(log/Gamma(/sum^{K}_{j=1}/alpha_j)-/sum^{K}_{i=1}log/Gamma(/alpha_i))+/sum^{K}_{i=1}((/alpha_i-1)(/psi(/gamma_{di})-/psi(/sum^{K}_{j=1}/gamma_{dj})))
$$
求导，得到：
$$
/frac{/partial{/mathcal{L}}}{/partial{/alpha_{i}}}=N(/psi(/sum^{K}_{j=1}/alpha_j)-/psi/alpha_i)+/sum^{N}_{d=1}(/psi(/gamma_{di}-/psi(/sum^{K}_{j=1}/gamma_{dj}))
$$
无法直接令导数等于0计算出$/alpha_i$。
计算出Hessian矩阵：
$$
/frac{/partial^{2}/mathcal{L}}{/partial{/alpha_{i}}/partial{/alpha_{j}}}=N(/psi{‘}(/sum^{K}_{j=1})-/delta(i,j)/psi{‘}(/alpha_i))
$$
使用牛顿法来优化$/alpha$。

LDA的实现

python实现的Variational EM LDA。用于训练和预测的数据集分别放在两个文本文件中，一行表示一篇文档，可处理中文和英文。
下面给出代码。本代码参考了David M.Blei的c语言源码。
变分推断以及EM的收敛条件可以通过计算likelihood来实现，这里设置了固定的循环次数。超参数alpha的更新被省略了，使用了初始值。
几个重要参数的对应关系见下表。

公式符号	代码符号	描述
$/alpha$	alpha	模型参数，document-topic分布的超参数
$/varphi$	varphi	模型参数，topic-word分布，代码中取了对数
$/gamma$	gamma	变分参数，当前推断文档的topic分布
$/phi$	phi	变分参数，当前推断文档的每个词语的topic分布

本代码先用训练数据训练得到一个模型，输出了得到的每个topic的top10的词语，然后对新来的测试文档进行了推断，通过$/gamma$参数得到预测的该文档属于的主题。

import numpy as np
import codecs
import jieba
import re
import random
import math
from scipy.special import psi

# itemIdList : the list of distinct terms in the document
# itemCountList : the list of number of the existence of corresponding terms
# wordCount : the number of total words (not terms)
class Document:
    def __init__(self, itemIdList, itemCountList, wordCount):
        self.itemIdList = itemIdList
        self.itemCountList = itemCountList
        self.wordCount = wordCount

# preprocessing (segmentation, stopwords filtering, represent documents as objects of class Document)
def preprocessing():
    
    # read the list of stopwords
    file = codecs.open('stopwords.dic','r','utf-8')
    stopwords = [line.strip() for line in file]
    file.close()
    
    # read the corpus for training
    file = codecs.open('dataset.txt','r','utf-8')
    documents = [document.strip() for document in file] 
    file.close()
    
    docs = []
    word2id = {}
    id2word = {}
    
    currentWordId = 0
    for document in documents:
        word2Count = {}
        # segmentation
        segList = jieba.cut(document)
        for word in segList: 
            word = word.lower().strip()
            # filter the stopwords
            if len(word) > 1 and not re.search('[0-9]', word) and word not in stopwords:
                if word not in word2id:
                    word2id[word] = currentWordId
                    id2word[currentWordId] = word
                    currentWordId += 1
                if word in word2Count:
                    word2Count[word] += 1
                else:
                    word2Count[word] = 1
        itemIdList = []
        itemCountList = []
        wordCount = 0

        for word in word2Count.keys():
            itemIdList.append(word2id[word])
            itemCountList.append(word2Count[word])
            wordCount += word2Count[word]

        docs.append(Document(itemIdList, itemCountList, wordCount))

    return docs, word2id, id2word
    
def maxItemNum():
    num = 0
    for d in range(0, N):
        if len(docs[d].itemIdList) > num:
            num = len(docs[d].itemIdList)
    return num

def initialLdaModel():
    for z in range(0, K):
        for w in range(0, M):
            nzw[z, w] += 1.0/M + random.random()
            nz[z] += nzw[z, w]
    updateVarphi()    

# update model parameters : varphi (the update of alpha is ommited)
def updateVarphi():
    for z in range(0, K):
        for w in range(0, M):
            if(nzw[z, w] > 0):
                varphi[z, w] = math.log(nzw[z, w]) - math.log(nz[z])
            else:
                varphi[z, w] = -100

# update variational parameters : gamma and phi
def variationalInference(docs, d, gamma, phi):
    phisum = 0
    oldphi = np.zeros([K])
    digamma_gamma = np.zeros([K])
    
    for z in range(0, K):
        gamma[d][z] = alpha + docs[d].wordCount * 1.0 / K
        digamma_gamma[z] = psi(gamma[d][z])
        for w in range(0, len(docs[d].itemIdList)):
            phi[w, z] = 1.0 / K

    for iteration in range(0, iterInference):
        for w in range(0, len(docs[d].itemIdList)):
            phisum = 0
            for z in range(0, K):
                oldphi[z] = phi[w, z]
                phi[w, z] = digamma_gamma[z] + varphi[z, docs[d].itemIdList[w]]
                if z > 0:
                    phisum = math.log(math.exp(phisum) + math.exp(phi[w, z]))
                else:
                    phisum = phi[w, z]
            for z in range(0, K):
                phi[w, z] = math.exp(phi[w, z] - phisum)
                gamma[d][z] =  gamma[d][z] + docs[d].itemCountList[w] * (phi[w, z] - oldphi[z])
                digamma_gamma[z] = psi(gamma[d][z])


# calculate the gamma parameter of new document
def inferTopicOfNewDocument():
    testDocs = []
    # read the corpus to be inferred
    file = codecs.open('infer.txt','r','utf-8')
    testDocuments = [document.strip() for document in file] 
    file.close()
    
    for d in range(0, len(testDocuments)):
        document = testDocuments[d]
        word2Count = {}
        # segmentation
        segList = jieba.cut(document)
        for word in segList: 
            word = word.lower().strip()
            if word in word2id:
                if word in word2Count:
                    word2Count[word] += 1
                else:
                    word2Count[word] = 1
                      
        itemIdList = []
        itemCountList = []
        wordCount = 0

        for word in word2Count.keys():
            itemIdList.append(word2id[word])
            itemCountList.append(word2Count[word])
            wordCount += word2Count[word]

        testDocs.append(Document(itemIdList, itemCountList, wordCount))
    
    gamma = np.zeros([len(testDocuments), K])
    for d in range(0, len(testDocs)):
        phi = np.zeros([len(testDocs[d].itemIdList), K])
        variationalInference(testDocs, d, gamma, phi)
        
    return gamma
           
docs, word2id, id2word = preprocessing() 

    
# number of documents for training
N = len(docs)
# number of distinct terms
M = len(word2id)
# number of topic
K = 10
# iteration times of variational inference, judgment of the convergence by calculating likelihood is ommited
iterInference = 20 
# iteration times of variational EM algorithm, judgment of the convergence by calculating likelihood is ommited
iterEM = 20

# initial value of hyperparameter alpha
alpha = 5
# sufficient statistic of alpha
alphaSS = 0
# the topic-word distribution (beta in D. Blei's paper)
varphi = np.zeros([K, M])
# topic-word count, this is a sufficient statistic to calculate varphi
nzw = np.zeros([K, M])
# topic count, sum of nzw with w ranging from [0, M-1], for calculating varphi
nz = np.zeros([K])

# inference parameter gamma
gamma = np.zeros([N, K])
# inference parameter phi
phi = np.zeros([maxItemNum(), K])

# initialization of the model parameter varphi, the update of alpha is ommited
initialLdaModel()

# variational EM Algorithm
for iteration in range(0, iterEM): 
    nz = np.zeros([K])
    nzw = np.zeros([K, M])
    alphaSS = 0
    # EStep
    for d in range(0, N):
        variationalInference(docs, d, gamma, phi)
        gammaSum = 0
        for z in range(0, K):
            gammaSum += gamma[d, z]
            alphaSS += psi(gamma[d, z])
        alphaSS -= K * psi(gammaSum)

        for w in range(0, len(docs[d].itemIdList)):
            for z in range(0, K):
                nzw[z][docs[d].itemIdList[w]] += docs[d].itemCountList[w] * phi[w, z]
                nz[z] += docs[d].itemCountList[w] * phi[w, z]

    # MStep
    updateVarphi()

# calculate the top 10 terms of each topic
topicwords = []
maxTopicWordsNum = 10
for z in range(0, K):
 ids = varphi[z, :].argsort()
 topicword = []
 for j in ids:
  topicword.insert(0, id2word[j])
 topicwords.append(topicword[0 : min(10, len(topicword))])

# infer the topic of each new document
inferGamma = inferTopicOfNewDocument()
inferZ = []
for i in range(0, len(inferGamma)):
    inferZ.append(inferGamma[i, :].argmax())

实验结果

继续沿用了前面用过的数据集，英文数据集采用关于one piece的16个英文文档，来源于维基百科。
设置的参数为K=10，iterInference=20，iterEM=20。
实验结果如下图。给出了每个主题top10的词语。
自然语言处理之LDA II-Variational EM实现
此外用于预测的两个文档见下图，这两句话不在训练集之中，是新写的两句话，分别被预测为了主题7和主题2，对比上面的图可以看出预测的十分正确。

当然，如果需要预测主题的文档中的大多数词都没在训练集中出现过，比如你用英文文档来训练，用中文文档来预测，那么预测的结果肯定是不对的。