转载

机器学习中引入L2范数的意义是什么？

其他几位的解释都比较好了，简而言之就是：L1是假设参数服从双指数分布，利于保证权值向量的稀疏性；L2是假设参数服从高斯分布，利于防止过拟合。

由于大部分场景下，我们都是对于单目标值进行训练，即求权值向量的L2值（权值向量的模的大小），然而在多目标值训练时，我们要求解权值矩阵的L2值，怎么求？意义是什么？

我的一篇博文中进行了说明：

关于线性模型你可能还不知道的二三事（三、特征值与奇异值的魔力）

系列

关于线性模型你可能还不知道的二三事（一、样本）
关于线性模型你可能还不知道的二三事（二、也谈民主）
关于线性模型你可能还不知道的二三事（三、特征值与奇异值的魔力）

目录 1 L2惩罚项

1.1 惩罚项

1.2 L2惩罚项与过拟合

1.3 多目标值线性模型

2 特征值分解

3 奇异值分解

4 总结

5 参考资料

1 L2惩罚项

1.1 惩罚项 为了防止世界被破坏，为了维护世界的和平……不好意思，这篇一开头就荒腔走板！某些线性模型的代价函数包括惩罚项，我们从书本或者经验之谈中学习到惩罚项主要有两个作用：为了防止模型过拟合，为了维护模型的简洁性。常见的惩罚项有L0、L1和L2惩罚项，其中L0惩罚项为权值向量W中不为0的分量个数，L1惩罚项为权值向量W各分量的绝对值之和，这两个惩罚项皆可以很好地维持权值W的稀疏性。单目标值时，L2惩罚项为权值向量W的模，多目标值时，L2惩罚项为权值矩阵W的奇异值的最大值，L2惩罚项可以很好地防止模型过拟合。在《机器学习中的范数规则化之（一）L0、L1与L2范数》中，作者直观地说明了为什么L1在维持简洁性上更具优势，而L2在防止过拟合上力压群芳。

更进一步说，带惩罚项的线性模型的求解过程本质上是解含先验信息的极大似然估计。含有L1惩罚项的线性模型，其假设权值向量W服从双指数分布；含有L2惩罚项的线性模型，其假设权值向量服从高斯分布。在另外的博文中，我将进一步说明其中的奥义。

1.2 L2惩罚项与过拟合 L0惩罚项本就是最原始的模型简洁性的表示，L1以及单目标值L2惩罚项的几何意义都比较显见，我们也很容易从几何角度上深刻地理解其对防止过拟合或者维持简洁性的原理。在本文中，我们主要关注L2惩罚项。

过拟合现象，通俗来说就是模型过于适合训练数据，而在待预测数据上性能不好的现象。然而，真正发生过拟合，是数据和模型两个方面共同作用造成的：数据在抽样时可能并不能代表整体，甚至与整体有较大的差异，而足够复杂的模型在这样的数据上训练后，将会产生过拟合现象。例如：在整体中，第i个特征与目标值并没有很强的相关性（平均情况），但是抽样偏偏把那些有强相关性的个体抽了出来，若在此数据上训练未剪枝的决策树模型，其很难对新的待预测数据做出准确的判断。

单目标值L2惩罚项表示为权值向量W的模的大小，当线性模型的代价函数中加入单目标值L2惩罚项后，一方面，为了更好地符合训练数据，学习的本质促使各特征之间的差异性增大，即权值向量W的各分量之间的差异增大；另一方面，为了满足惩罚项，权值向量W的模必须受限小于一定范围，也就意味着权值向量W的每个分量都受限小于一定范围，分量之间的差异性就不会过于明显。如此以来，我们可以用“瞻前顾后”来形容带惩罚项的线性模型的训练过程。

然而，多目标值L2惩罚项的意义就不那么好理解了：权值矩阵W的奇异值的最大值是什么鬼？

1.3 多目标值线性模型 要知道多目标值L2惩罚项的意义，我们先要知道多目标值的线性模型是什么？简单来说，多目标值线性模型是多个单目标值线性模型的组合（这不是废话嘛……），也就是权值向量W变成了权值矩阵W，而目标值向量y变成了目标值矩阵Y。样本容量为m，特征个数为n，目标值个数为l的多目标值线性模型表示如下：

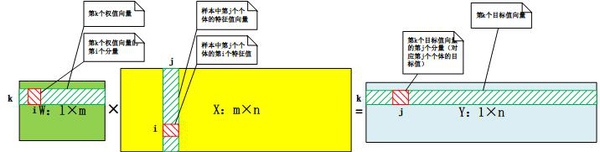
从上图我们可以看到，由权值矩阵的第k个行向量和样本的特征矩阵X将生成目标值矩阵的第k个行向量。

2 特征值分解 还是让我们简化一下模型：设目标值个数l等于样本容量m。这时，权值矩阵W变成了m阶方阵。

可能为了学分，为了考研，我们都学习过如何进行特征值分解，也刷过不少的相关习题。但是，可能有很大一部分不理解为什么要特征值分解，其有什么几何意义？首先，让我们回归本质，从定义中得到特征值和特征向量有如下性质：

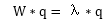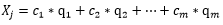特征向量是一组特殊的向量，其通过原矩阵W（在本文中是权值矩阵）进行行变换后，不会改变放心，只会改变大小，而缩放的程度为其对应的特征值大小。另外，我们总是找到一组m个线性无关的特征向量，于是可以将个体Xj表示成：机器学习中引入L2范数的意义是什么？

在线性模型的定义中，我们需要将权值矩阵W右乘样本的特征矩阵X，对于个体Xj来说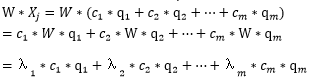：机器学习中引入L2范数的意义是什么？

不难发现，经过权值矩阵W右乘后的样本与原始样本相比，其仅仅在各特征向量方向上进行了伸缩，伸缩的程度为对应的特征值大小。从几何的角度来说，矩阵W右乘向量Xj，本质是在特征向量组成的m维空间里进行缩放。

此时，我们再看，到底什么决定着个体Xj的目标值呢？如果某个特征值的绝对值过大，个体Xj的目标值就会近似于对应的伸缩后特征向量。以下3阶的例子很好地进行了说明：

有3个特征向量q1、q2和q3，对应特征值为1、5和1。Xj表示为(2,2,2) ，W*Xj等于(2,6,6)，该目标值近似于特征向量q2伸长了5倍后的结果。通过该例，我们得知，当权值矩阵W为方阵时，特征值绝对值的最大值决定了目标值的偏向性（偏向于对应的伸缩后的特征向量），所以，当特征值绝对值的最大值很大时，那么待预测的样本经过权值矩阵W右乘后，都会偏向于对应的伸缩后的特征向量，这样变造成了过拟合的现象：偏向性体现了在训练数据上的尽力符合，但是却和实际情况并不相符。上式中，v为W自乘后（m阶）进行特征值分解的特征向量，lambda为对应的特征值开方（奇异值），u为l维的列向量。与特征值分解不同的是，特征向量q变成了v向量和u向量。我们可以理解，通过W右乘后，m维的v向量其在l维空间中的一一对应u向量，不会发生方向上的变化，仅仅进行伸缩。于是，同样我们可以对样本进行重新表示和计算：还是同样的配方，还是熟悉的味道，我们可以用奇异值的最大值用来表示任意权值矩阵W的L2惩罚项。

矩阵问题的推导，很多时候都是从方阵开始，然后到任意矩阵。特征值分解和奇异值分解刻画了矩阵对向量（或矩阵）的转换作用，特征值（奇异值）描绘了转换力度，特征向量描绘了转换方向，特征值分解的转换在同一空间中，而奇异值分解的转换在两个不同空间中进行。

原文 http://dataunion.org/25011.html

正文到此结束