转载

在Python中利用Theano训练神经网络

【译文】在Python中利用Theano训练神经网络

作者 Aarshay Jain

译者钱亦欣

引言

我最新的文章讨论了一些深度学习的基础知识，其中对人工神经网络也进行了一些简要说明。现在就让我们对于在Python中调用Theano训练神经网络做一个操作说明。

神经网络可以用诸如Caffe，Torch，TensorFlow等库来实现，但用Theano可能更为方便全面，并且它的诸多特性可以帮助提升后续的Python编码体验。

本文中，我将提供一个通俗易懂的操作指南，如果你只是想要建模的Python代码，大可以跳过中间的说明部分。但如果你之前没用过Theano，我建议通读全文来获得全面的理解。

注：

本文最适合那些有一定神经网络和深度学习基础的读者。

如果你没有Python基础，请从此开始阅读。

如果你不了解深度学习，请从这里开始。

全文目录

Theano简介
执行简单表式
Theano变量类型
Theano函数
单个神经元
双层神经网络

1. Theano简介

简而言之，Theano是：

一种基于Python的编程语言，有着与numpy紧密相关的数据结构。

在后端利用C语言的线性代数编译器

一个快速实现数学表达式的Python库

众所周知，Theano由蒙特利尔大学于2008年开发，是一种用于定义并执行数学表达式的工具。

Theano有着诸多特性可对执行时间进行优化。比如将符号表达式变形后再转化为C代码，如下：

为了加速表达式的编译，它将{（x+y）+（x+y）}转化为{2*（x+y）}

为了使表达式更稳定，它将{ exp(a) / exp(a).sum(axis=1) } 转化为{ softmax(a) }

下面是使用Theano的一些优势：

１.它为不同的数学表达式定义了C代码。

２.相较Python的一些默认实现方法，利用Theano速度更快。

３.由于执行速度更快，它可以解决一些高维问题。

４.它可以使用GPU进行计算，实现深度学习速度极快。

现在让我们结合案例来理解Theano这种语言。

实现简单的表达式

让我们从执行简单的数学表达式开始，看看Theano系统是如何运作的。我们将深入了解每个单元，最常规的Theano代码结构按照以下三部分编写：

1. 定义变量/对象

2. 用函数形式定义数学表达式

3. 通过传递变量值来执行表达式

让我们根据下列带来实现简单的两数相乘：

Step 0：加载库

import numpy as np import theano.tensor as T from theano import function

从theano库中我们加载了两个重要函数，function和tensor。

Step 1：定义变量

a = T.dscalar('a') b = T.dscalar('b')

这里定义了两个变量，请注意此处我们使用的是tensor对象类型。同样，传递给dscalar函数的仅仅是张量的名字，这在后续调试时会很有用。即使没有它们，这些代码也可以正常执行。（译者注：原文疑似有拼写错误）

Step 2：定义表达式

c = a*b f = function([a,b],c)

这里我们定义了一个双参数函数，[a, b]是输入，c是先前定义好的输出。

Step 3：执行表达式

f(1.5,3)

array（4.5）

现在我们就通过输入两个数值调用了这个函数，并且得到了两数乘积作为输出。我们现在已经快速了解如何在Theano中定义数学表达式并执行它们了。在学习复杂函数之前，我们先来学习Theano的一些固有属性，它们对于将来构建神经网络会很有用。

3. Theano变量类型

变量是任何一种编程语言的关键模块。Theano中，对象都被定义为张量。张量可以简单理解为t维的向量，不同维度就对应着不同的类型：

t = 0: 标量

t = 1: 向量

t = 2: 矩阵

...

通过这个有趣的视频（译者注：油管，需要翻墙），你会对向量和张量有更深入的理解。

这些变量可以与先前代码中我们定义的dscalar类比。先前定义变量的关键词是：

byte: bscalar, bvector, bmatrix, brow, bcol, btensor3, btensor4
16-bit integers: wscalar, wvector, wmatrix, wrow, wcol, wtensor3, wtensor4
32-bit integers: iscalar, ivector, imatrix, irow, icol, itensor3, itensor4
64-bit integers: lscalar, lvector, lmatrix, lrow, lcol, ltensor3, ltensor4
float: fscalar, fvector, fmatrix, frow, fcol, ftensor3, ftensor4
double: dscalar, dvector, dmatrix, drow, dcol, dtensor3, dtensor4
complex: cscalar, cvector, cmatrix, crow, ccol, ctensor3, ctensor4

现在你知道了我们可以用不同的维度和内存分配来定义变量。但这个列表也并不完整，我们可以定义高于4维的张量型的类。在这里你可以发现更多细节。

请记住这些类型的变量只是一个符号。他们没有任何固定取值，并且以符号的形式传入函数。只有在函数被调用时它们才取具体数值。但我们常常需要一些常量变量和一些不必传入所有函数的变量。为解决这些需求，Theano提供了共有变量。这些变量有固定取值并且不属于上述说明的任何类型。它们可以定义为numpy数据类型或者是简单的常量。

让我们举个例子：假设我们初始化了一个取值为0的共有变量，并且使用如下函数：

接受一个输入
将输入值添加到共有变量
返回共有变量的平方

以上过程可以通过如下方式实现：

from theano import shared x = T.iscalar('x') sh = shared(0) f = function([x], sh**2, updates=[(sh,sh+x)])

注意这里的含有有一个额外的参数updates。它得是一个以列表或元组为元素的列表，每个都要包含shared_variable和updated_value两个元素。下列3个案例的输出如下：

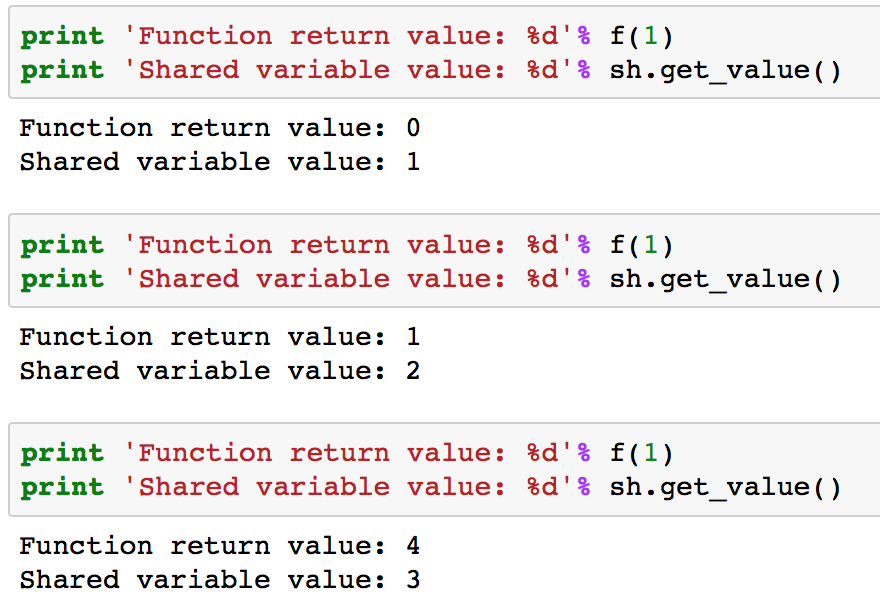
在Python中利用Theano训练神经网络

你可以发现，每次执行这个函数它都会返回当前值的平方，即更新前的值。每次运行后，共有变量的值就被跟新了。同样的，共有指标有两个函数操作，get_value()和set_value()用来读取和修改共有变量的值。

4. Theano 函数

目前为止我们已经了解了Theano中基本的函数结构和变量处理。现在让我们讨论关于函数的其他内容：

返回多个值

我们可以让一个函数返回多个值。通过下面的例子你很快就能掌握：

a = T.dscalar('a') f = function([a],[a**2, a**3]) f(3)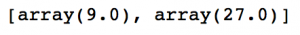

在Python中利用Theano训练神经网络

输出是一个包含函数输入值平方和立方值的数组。

计算梯度

梯度的计算是深度学习的一大重点。在Theano实现该功能也很容易，让我们定义一个函数计算变量的立方值并返回相应的梯度。

x = T.dscalar('x') y = x**3 qy = T.grad(y,x) f = function([x],qy) f(4)

上述代码返回值为48也就是在x=4时三次函数的梯度值。Theano对于这个过程有很漂亮的输出：

from theano import pp  #pretty-print print(pp(qy))

在Python中利用Theano训练神经网络

简而言之，它可以解释为 fill(x^3,1)×3×x^(3-1),这恰好就是3×x^3的梯度值。fill(x^3,1)的意思是生成一个和x^3同维度的矩阵，并把其所有元素填充为1.它主要在高维输入中发挥作用，但在本例里可以忽略不计。

我们还可以用Theano计算Jacobian矩阵和Hessian矩阵，参考此文。

Theano还有诸如条件结构和循环结构的内容，你可以通过以下资源进一步学习：

Theano Conditional Constructs
Theano Looping Statements
Handling Shape Information

5. 训练单个神经元

让我们从单个神经元起步

我会引用先前的文章中的案例，如果你想要了解更多细节，请阅读这篇文章。为了构建一个神经元，需要如下两步：

实现前向反馈传递
- 接受输入并决定输出
- 本例使用固定权重
执行逆向反馈
- 计算误差和梯度值
- 利用梯度值更新权重

让我们实现实现一个“与”门（逻辑运算）。

前向反馈传递

“与”门可以这么实现：

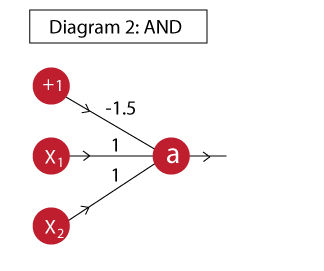
在Python中利用Theano训练神经网络

现在我们来定义一个前馈网络，它接受输出并用如上权重计算输出。首先我们定义单个神经元来计算输出a

import theano import theano.tensor as T from theano.ifelse import ifelse import numpy as np  # 定义变量: x = T.vector('x') w = T.vector('w') b = T.scalar('b')  # 定义数学表达式: z = T.dot(x,w)+b a = ifelse(T.lt(z,0),0,1)  neuron = theano.function([x,w,b],a)

我很容易地实现了上述过程，如果你对这些表达式不熟悉，请参考我之前的神经网络文章。现在我们看看输出来确定模型是否真的实现了逻辑运算。

# 定语输入与权重 inputs = [     [0, 0],     [0, 1],     [1, 0],     [1, 1] ] weights = [ 1, 1] bias = -1.5  # 遍历所有输入并输出结果: for i in range(len(inputs)):     t = inputs[i]     out = neuron(t,weights,bias)     print 'The output for x1=%d | x2=%d is %d' % (t[0],t[1],out)

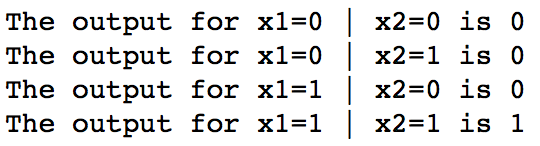
在Python中利用Theano训练神经网络

请注意，这个案例中我们在调用函数时需要提供权重。然而权重在模型训练过程需要被不断更新，因此最好把它们定义为共有变量。试试这一改动，输出应该是一样的。

import theano import theano.tensor as T from theano.ifelse import ifelse import numpy as np  # 定义变量: x = T.vector('x') w = theano.shared(np.array([1,1])) b = theano.shared(-1.5)  # 定义数学表达式: z = T.dot(x,w)+b a = ifelse(T.lt(z,0),0,1)  neuron = theano.function([x],a)  # 定义输入和权重 inputs = [     [0, 0],     [0, 1],     [1, 0],     [1, 1] ]  # 遍历所有输入并得到输出: for i in range(len(inputs)):     t = inputs[i]     out = neuron(t)     print 'The output for x1=%d | x2=%d is %d' % (t[0],t[1],out)

现在前向反馈步骤已经完成了。

逆向传播

现在让我们修改之前的代码，在其中添加如下流程：

基于输出的真值计算损失函数值
计算每个节点的梯度
利用梯度值跟新权重

我们先初始化网络：

# 梯度 import theano import theano.tensor as T from theano.ifelse import ifelse import numpy as np from random import random  # 定义变量: x = T.matrix('x') w = theano.shared(np.array([random(),random()])) b = theano.shared(1.) learning_rate = 0.01  # 定义数学表达式: z = T.dot(x,w)+b a = 1/(1+T.exp(-z))

与之前的程序相比，这段代码最大的不用就是x被定义为矩阵而不是向量。通过这种处理，所有的输出可以一起被计算，并且总损失值也可以一次性计算出来。

你应当牢记这里我使用了full-batch梯度下降法，也就是说使用所有训练样本来跟新权重。

通过如下代码可以计算损失：

a_hat = T.vector('a_hat') #Actual output cost = -(a_hat*T.log(a) + (1-a_hat)*T.log(1-a)).sum()

这段代码中我们定义a_hat为实际观测值，让后用简单的逻辑斯底损失函数计算损失（因为是个分类问题）。现在让我们来计算梯度，并定义权重更新方法。

dw,db = T.grad(cost,[w,b])  train = function(     inputs = [x,a_hat],     outputs = [a,cost],     updates = [         [w, w-learning_rate*dw],         [b, b-learning_rate*db]     ] )

此处，我们先用权重和偏差值计算出损失值，再以此计算梯度。train函数实现了权重更新功能。将权重定义为共有变量是非常巧妙而优雅的方法，通过这种技巧更新后的权重将自动传入模型。

# 定义输入和权重 inputs = [     [0, 0],     [0, 1],     [1, 0],     [1, 1] ] outputs = [0,0,0,1]  # 遍历所有输入并计算输出: cost = [] for iteration in range(30000):     pred, cost_iter = train(inputs, outputs)     cost.append(cost_iter)  # 打印输出: print 'The outputs of the NN are:' for i in range(len(inputs)):     print 'The output for x1=%d | x2=%d is %.2f' % (inputs[i][0],inputs[i][1],pred[i])  # 绘制损失图: print '/nThe flow of cost during model run is as following:' import matplotlib.pyplot as plt %matplotlib inline plt.plot(cost)

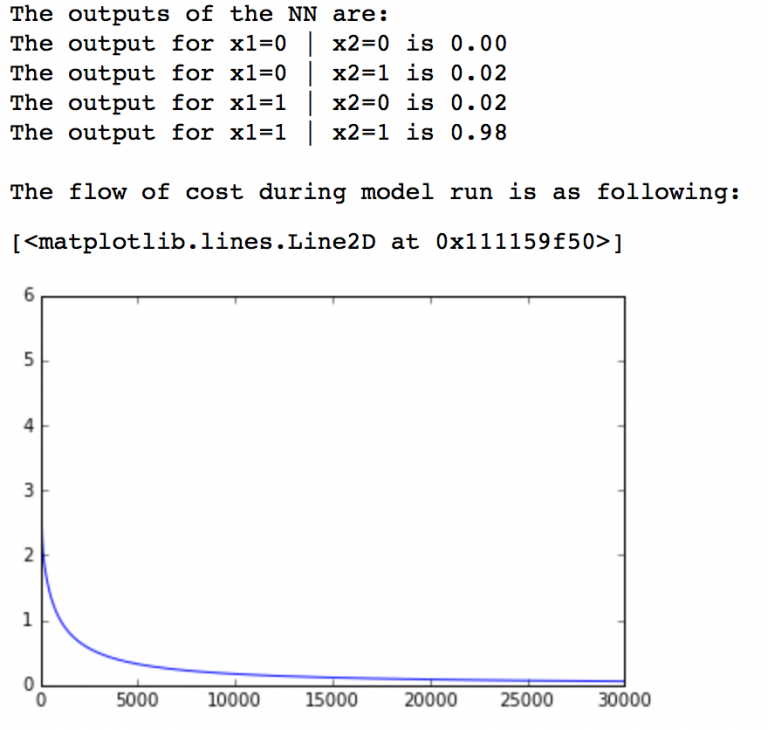
在Python中利用Theano训练神经网络

这里我们简单定义了一些输入和输出值并训练了模型。训练过程中我们也记录了每次迭代的损失值并将其绘制。通过图我们可以发现损失值很快就下降到了一个比较低的水平。模型的输出值和真值也十分接近，我们成功训练了单个神经元。

6. 训练双层神经网络

我希望你已经了解了上述的内容，如果没有请反复阅读再看这部分，这将帮助你更深入地理解神经网络。

让我们用2层神经网络的例子强化理解。为了尽可能地简单，我将用前文的XNOR（同或门）做例子。如果你想要知道更多细节，请读读这篇文章。

XNOR函数可以这么实现：

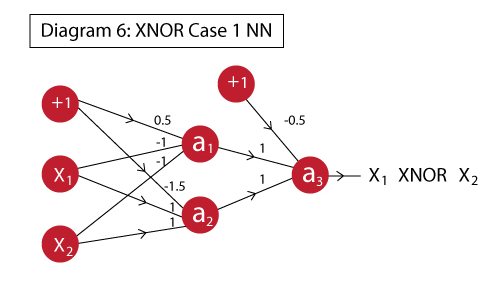
在Python中利用Theano训练神经网络

友情提醒，XNOR函数的真值表应该是这样的：

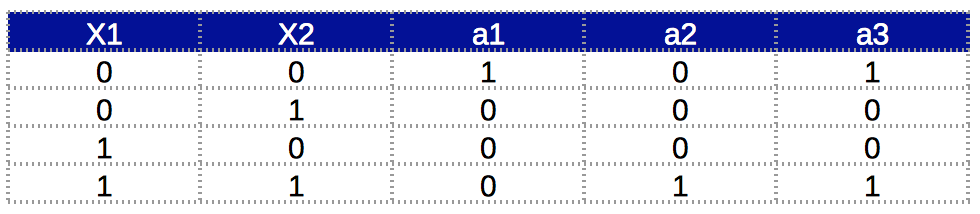
在Python中利用Theano训练神经网络

现在我们可以一次性实现前向反馈和逆向反馈。

Step1 定义变量

import theano import theano.tensor as T from theano.ifelse import ifelse import numpy as np from random import random  # 定义变量: x = T.matrix('x') w1 = theano.shared(np.array([random(),random()])) w2 = theano.shared(np.array([random(),random()])) w3 = theano.shared(np.array([random(),random()])) b1 = theano.shared(1.) b2 = theano.shared(1.) learning_rate = 0.01

这步中我们定义了所有变量，请注意，针对每个神经元我们现在有个3个权重向量，2个偏差值单元（由于有两层）。

Step2 定义数学表达式

a1 = 1/(1+T.exp(-T.dot(x,w1)-b1)) a2 = 1/(1+T.exp(-T.dot(x,w2)-b1)) x2 = T.stack([a1,a2],axis=1) a3 = 1/(1+T.exp(-T.dot(x2,w3)-b2))

我们对于每个神经元定义了相应的表达式，为了计算X2需要多定义一个表达式。这样a1和a2的输出就能整合到一个矩阵中，该矩阵的点积就可以作为权重向量。

让我们多做一点点探索。a1，a2都会返回一个四维向量，如我们我们用数组存储它们，就会得到[ [a11,a12,a13,a14], [a21,a22,a23,a24] ]这样的结构。然而，我们偏爱的结构是 [ [a11,a21], [a12,a22], [a13,a23], [a14,a24] ]。Theano中的stacking函数可以实现这一需求。

Step3 定义梯度和更新准则

a_hat = T.vector('a_hat') #Actual output cost = -(a_hat*T.log(a3) + (1-a_hat)*T.log(1-a3)).sum() dw1,dw2,dw3,db1,db2 = T.grad(cost,[w1,w2,w3,b1,b2])  train = function(     inputs = [x,a_hat],     outputs = [a3,cost],     updates = [         [w1, w1-learning_rate*dw1],         [w2, w2-learning_rate*dw2],         [w3, w3-learning_rate*dw3],         [b1, b1-learning_rate*db1],         [b2, b2-learning_rate*db2]     ] )

这段和先前的很类似，关键的不同点就是我们现在计算3个权重向量，2个偏差单元的梯度，再进行更新。

Step4 训练模型

inputs = [     [0, 0],     [0, 1],     [1, 0],     [1, 1] ] outputs = [1,0,0,1]  # 遍历输入并计算输出: cost = [] for iteration in range(30000):     pred, cost_iter = train(inputs, outputs)     cost.append(cost_iter) # 打印输出     print 'The outputs of the NN are:' for i in range(len(inputs)):     print 'The output for x1=%d | x2=%d is %.2f' % (inputs[i][0],inputs[i][1],pred[i])  # 绘制损失图: print '/nThe flow of cost during model run is as following:' import matplotlib.pyplot as plt %matplotlib inline plt.plot(cost)

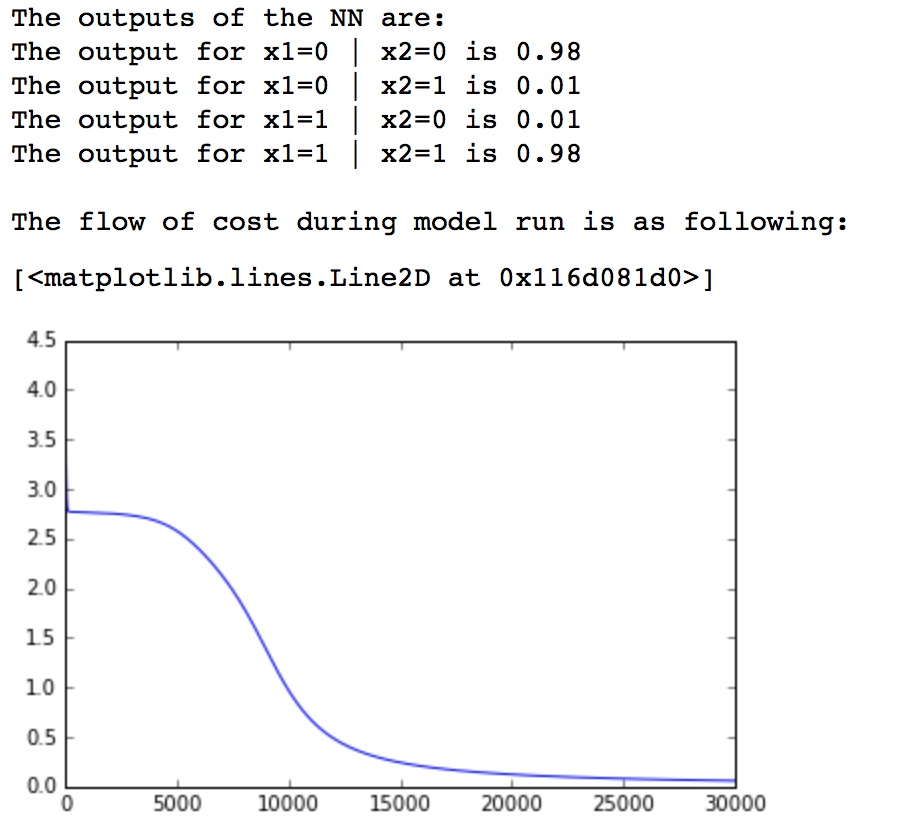
在Python中利用Theano训练神经网络

我们可以看到我们训练的神经网络成功实现了XNOR函数功能。模型的损失也下降到了合理的水平，通过上述事实，我们成功实现了一个2层神经网络。

结语

通过本文我们了解了Python中Theano模块的基本使用方法，并知道了它如何作为编程语言发挥作用。我们也用它训练了一些简单的神经网络模型。我确信利用它训练模型能加深你对神经网络的理解。

如果你坚持读到了这里，你真该奖励你自己。Theano和sklearn之类的模块不大一样，学起来并不容易。但神经网络的魅力就在于它的灵活性，利用Theano可以让你更自由地设定模型。我知道市面上已经有封装的很好的Theano库，比如Keras和Lasagne，但我认为了解Theano的内核对你会很有帮助。