转载

堆栈 2 - 应用 1

继续是《数据结构算法与应用：C++语言描述》的笔记，继续第五章堆栈的内容，这节是最后关于应用方面的内容。这节先介绍括号的匹配，汉诺塔，火车车厢重排三个问题。

括号的匹配

括号的匹配就是要匹配一个字符串中的左、右括号。目标是编写一个C++程序，其输入为一个字符串，输出为相互匹配的括号以及未能匹配的括号。注意，括号匹配问题可用来解决C++程序中的{和}的匹配问题。

可以观察到，如果从左至右扫描一个字符串，那么最近每个右括号将于最近遇到的未匹配的左括号相匹配。因此，我们可以在从左至右的扫描过程中，把所遇到的左括号放到堆栈内，每当遇到一个右括号时，就将它与栈顶的左括号(如果存在)相匹配，同时从栈顶删除该左括号。

下面给出括号匹配问题实现的代码，其时间复杂性是$/theta(n),其中n$是输入串的长度。

// 最大的字符串长度 const int MaxLength = 100; // 括号匹配 void PrintMatchedPairs(char* expr){     Stack<int> s(MaxLength);     int j, length = strlen(expr);     for (int i = 1; i <= length; i++){         // 从左到右扫描字符串         if (expr[i - 1] == '(')             // 栈中添加左括号的位置索引值             s.Add(i);         else if (expr[i - 1] == ')'){             try{                 s.Delete(j);                 cout << j << " " << i << endl;             }             catch (OutOfBounds){                 cout << "No match for right parenthesis" << " at " << i << endl;             }         }        }     // 堆栈中剩下的( 都是未匹配的     while (!s.IsEmpty()){         s.Delete(j);         cout << "No match for left parenthesis at " << j << endl;     } }

测试例子如下：

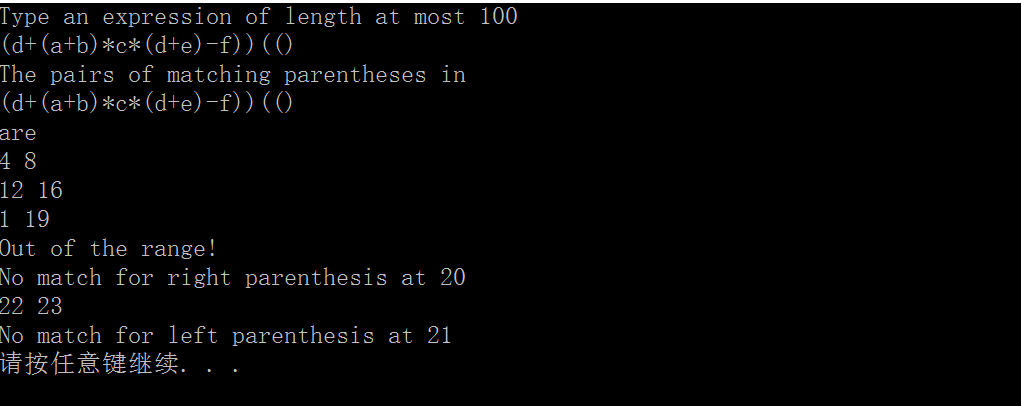
#include<iostream> #include"xcept.h" #include"Stack.h"  using std::cout; using std::endl; using std::cin;  void testMathedParis(){     // 测试括号匹配     char expr[MaxLength];     cout << "Type an expression of length at most " << MaxLength << endl;     cin.getline(expr, MaxLength);     cout << "The pairs of matching parentheses in " << endl;     puts(expr);     cout << "are" << endl;     PrintMatchedPairs(expr); }  int main(){      testMathedParis();      system("pause");     return 0; }

输出结果如下图所示：

汉诺塔

在汉诺塔问题中，已知有n个碟子和3座塔。初始时所有的碟子按从大到小次序从塔1的底部堆放至顶部，我们需要把碟子都移动到塔2，每次移动一个碟子，而且任何时候都不能把大碟放在小碟子的上面。

一个非常优雅的解决办法是使用递归。为了把最大的碟子移动到塔2，可以先将其余的n-1个碟子移动到塔3，然后把最大的碟子移动到塔2。接下来是把塔3上的n-1个碟子移动到塔2，因此要借用塔1和塔2，此时可以完全忽视塔2上已经有一个碟子的事实，因为这个碟子是所有碟子中最大的一个。

下面是按照递归方式实现的代码。初始调用的语句是 TowersOfHanoi(n,1,2,3)

// 汉诺塔问题,把n个碟子从塔x移动到塔y，可借助于塔z void TowersOfHanoi(int n, int x, int y, int z){     if (n > 0){         TowersOfHanoi(n - 1, x, z, y);         cout << "Move top disk from tower " << x << " to top of tower " << y << endl;         TowersOfHanoi(n - 1, z, y, x);     } }

该程序所花费的时间正比于所输出的信息行数目，而信息行的数目等价于碟子移动的次数，其碟子移动次数 moves(n) 如下所示：

moves(n)=

/begin{cases}

0 & n=0 //

2moves(n-1)+1 & n>0

/end{cases}

也就是有$moves(n)=2^n-1$,所以上述函数的时间复杂性是$/theta(2^n)$。

上述函数只是输出把碟子从塔1移动到塔2所需要的碟子移动次序。假定希望给出每次移动之后三座塔的状态，即塔上的碟子及其次序，那么必须在内存中保留塔的状态，并在每次移动碟子之后，修改塔的状态。

由于从每个塔上移走碟子时是按照LIFO的方式进行，因此可以把每个塔表示成一个堆栈。三座塔在任何时候都总共拥有n个碟子，因此，如果使用链表形式的堆栈，只需申请n个元素所需要的空间。如果使用的是基于公式化描述的堆栈，则塔1和塔2的容量都必须是n，而塔3的容量必须为n-1，因而所需要的空间总数为3n-1。

前面的分析指出，汉诺塔问题的复杂性是以n为指数的函数，因此在可以接受的时间范围内，只能解决n值比较小(如$n/le 30$)的汉诺塔问题。而对于这些较小的n值，基于公式化描述和基于链表描述的堆栈在空间需求上的差别相当小，因此可以随意使用。

下面给出基于公式化描述的堆栈。

#ifndef HANOI_H_ #define HANOI_H_  #include"Stack.h" #include<iostream>  class Hanoi{     friend void useTowersOfHanoi(int); public:     void TowersOfHanoi(int n, int x, int y, int z); private:     Stack<int> *S[4]; };  void Hanoi::TowersOfHanoi(int n, int x, int y, int z){     // 把n个碟子从塔x移动到塔y，可借助于塔z     // 碟子编号     int d;      if (n > 0){         TowersOfHanoi(n - 1, x, z, y);         // 从x中移动走一个碟子         S[x]->Delete(d);         // 放到y上         S[y]->Add(d);         ShowState();         TowersOfHanoi(n - 1, z, y, x);     } }  void useTowersOfHanoi(int n){     // 预处理程序     Hanoi X;     X.S[1] = new Stack<int>(n);     X.S[2] = new Stack<int>(n);     X.S[3] = new Stack<int>(n);      for (int d = n; d > 0; d--)         // 将碟子放到塔1上         X.S[1]->Add(d);      X.TowersOfHanoi(n, 1, 2, 3); } #endif

上述函数没有给出 ShowState() 方法的具体实现，这是由于该函数的实现取决于输出设备的性质（如计算机屏幕、打印机等）

火车车厢重排

一列货运列车共有n节车厢，每节车厢将停放在不同的车站。假定 n个车站的编号分别为1~n，货运列车按照第 n站至第1站的次序经过这些车站。车厢的编号与它们的目的地相同。为了便于从列车上卸掉相应的车厢，必须重新排列车厢，使各车厢从前至后按编号 1到n的次序排列。当所有的车厢都按照这种次序排列时，在每个车站只需卸掉最后一节车厢即可。

这里可以在一个转轨站里完成车厢的重排工作，在转轨站中有一个入轨、一个出轨和k个缓冲铁轨（位于入轨和出轨之间），如下图所示，其中有k=3个缓冲铁轨H1，H2，和H3。下图a是一个初始的袋重排的车厢次序，而图b则是按照要求的次序重排后的结果。

堆栈 2 - 应用 1

为了重排车厢，需从前至后依次检查入轨上的所有车厢。如果正在检查的车厢是下一个满足排列要求的车厢，可以直接把它放在出轨上。如果不是，则把它移动到缓冲铁轨上，直到按输出次序要求轮到它时才将它放到出轨上。缓冲铁轨是按照LIFO的方式使用的，因此车厢的进和出都是在缓存铁轨的顶部进行的。在重排车厢过程中，仅允许以下移动：

车厢可以从入轨的前部（即右端）移动到一个缓冲铁轨的顶部或者出轨的左端
车厢可以从缓冲铁轨的顶部移动到出轨的左端

考虑图a的情况，由于要求的次序是递增的方式，即1号是最先出轨，然后按顺序从2到9，因此在缓冲铁轨中也应该是从顶部到底部是递增的方式，即在顶部是编号小的，所以缓冲铁轨的中间状态如下所示：

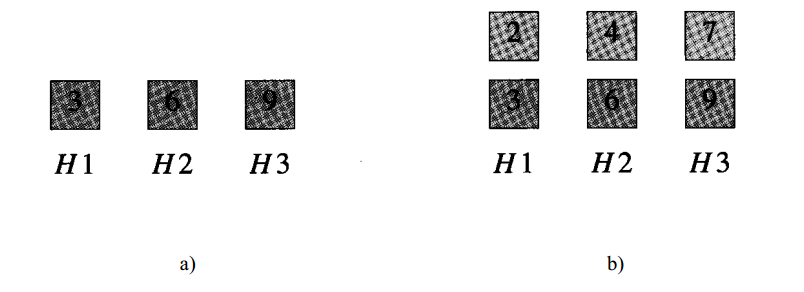
堆栈 2 - 应用 1

接下来剩下三个车厢，输出顺序就变得明了了。在这个分配过程中，主要是遵循这样一条规则：新的车厢u应送入这样的缓冲铁轨：其顶部的车厢编号v满足$v /gt u$，且v是所有满足这种条件的缓冲铁轨顶部车厢编号中最小的一个编号。

对于图a的例子，进行车厢重排的时候，只需要3个缓冲铁轨就足够了，但是对于其他的初始次序，可能需要更多的缓冲铁轨。

因此，这里使用k个链表形式的堆栈来描述k个缓冲铁轨。下列函数 Railroad 用于确定重排n个车厢，它最多可使用k个缓冲铁轨并假定车厢的次序为p[1:n]。如果不能成功重排，函数将返回false，否则返回true。具体实现如下所示：

// 火车车厢重排 bool Railroad(int p[], int n, int k){     // k个缓冲铁轨，车厢初始排序为p[1:n], 如果重排成功，返回true，否则返回false，如果内存不足，则引发异常NoMem     // 创建于缓冲铁轨对应的堆栈     LinkedStack<int> *H = new LinkedStack<int>[k+1];     // 下一次要输出的车厢     int NowOut = 1;     // 缓冲铁轨中编号最小的车厢     int minH = n + 1;     // minH号车厢对应的缓冲铁轨     int minS;     // 进行车厢重排     for (int i = 1; i <= n; i++){         if (p[i] == NowOut){             // 直接输出             cout << "More car " << p[i] << " from input to output" << endl;             NowOut++;             while (minH == NowOut){                 Output(minH, minS, H, k, n);                 NowOut++;             }         }         else{             // 将p[i]送入某个缓冲铁轨             if (!Hold(p[i], minH, minS, H, k, n))                 return false;         }     }     return true; }

下面则给出函数 Railroad 中使用的函数 Output和Hold 的代码实现，前者主要是用于将一节车厢从缓冲铁轨中输出到出轨处，同时修改minH和minS，而后者则是根据分配规则将车厢c送入某个缓冲铁轨，并在必要的时候修改minH和minS。

void Output(int& minH, int& minS, LinkedStack<int> H[], int k, int n){     // 把车厢从缓冲铁轨送至出轨处，同时修改minS和minH     // 车厢索引     int c;     // 从堆栈minS中删除编号最小的车厢minH     H[minS].Delete(c);     cout << "More car " << minH << " from holding track " << minS << " to output/n";     // 通过检查所有的栈顶，搜索新的minH和minS     minH = n + 2;     for (int i = 1; i <= k; i++){         if (!H[i].IsEmpty() && (c = H[i].Top()) < minH){             minH = c;             minS = i;         }     } }  bool Hold(int c, int& minH, int& minS, LinkedStack<int> H[], int k, int n){     // 在一个缓冲铁轨中放入车厢c,如果没有可用的缓冲铁轨，返回false，如果空间不足，则引发异常NoMem     // 目前最优的铁轨     int BestTrack = 0;     // 最优铁轨上的头辆车厢号     int BestTop = n + 1;     // 车厢索引     int x;     // 扫描缓冲铁轨     for (int i = 1; i <= k; i++){         if (!H[i].IsEmpty()){             x = H[i].Top();             if (c < x && x < BestTop){                 BestTop = c;                 BestTrack = i;             }         }         else{             // 铁轨是空             if (!BestTrack)                 BestTrack = i;         }     }     if (!BestTrack)         return false;     // 把车厢c送入缓冲铁轨     H[BestTrack].Add(c);     cout << "More car " << c << " from input to holding track " << BestTrack << endl;     // 必要时修改minH和minS     if (c < minH){         minH = c;         minS = BestTrack;     }     return true; }

上述两个函数Output和Hold的时间复杂性都是$/theta(k)$。而在函数Railroad中的while循环最多可以输出n-1节车厢，else语句也是最多有n-1节车厢被送入缓冲铁轨，因此，这两个函数所消耗的总时间是$O(kn)$。而Railroad函数中for循环部分的其余部分耗时$/theta(n)$,因此该函数的时间复杂性是$O(kn)$。

这里如果使用一个平衡折半搜索树来存储缓冲铁轨顶部的车厢编号（在第11章介绍），程序的复杂性可由将至$O(nlogk)$。

更详细的内容可以查看我的Github