关于递归的思考
之前有接触过递归，看到别人写的递归函数的代码，好生羡慕，怎么就能写这么好呢？我怎么就想不到这样写呢？如此等等。
就拿fibonacci函数来说吧，一个普通的函数可能这样写：
def fib(n): if n == 0: return 0 elif n == 1: return 1 else: return fib(n-1) + fib(n-2)
我看到这个函数的思考方式是这样的：
1. 当n=0时：返回0 2. 当n=1时：返回1 3. 当n=2时： 1. 首先去调用n=1，返回1 2. 再去调用n=0，返回0 3. 把0和1相加返回1 4. 当n=3时： 1. 调用n=2 1. 调用n=1，返回1 2. 调用n=0，返回0 3. 相加返回1 2. 调用n=1，返回1 3. 把1和1相加返回2 5. 等等
想到这我头都要爆了，彻底被人家的函数折服了，看来我是写不成这么好的函数了。
但我转念一想，这个函数的本质是fibnacci序列，我何不回归fibonacci本身呢？fibonacci用数学公式表示应该是这样：
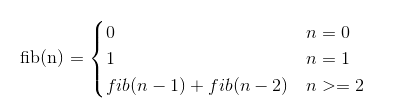
看到公式我恍然大悟，上面那个函数不就是根据这个公式直接翻译的嘛！原来我一直思考都是顺着函数的代码思考，这样肯定会觉得很难,
正确的思考方式应该是从算法出发然后再写代码。
经过了上面的惨痛教训看看我能不能写出正确的fibonacci序列函数，分段函数的公式应该是这样的：
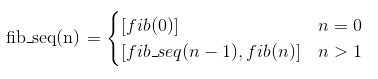
那么直接写成代码就应该是这样的:
def fib_seq(n): seq = [] if n == 0: seq.append(0) else: seq.extend(fib_seq(n-1)) seq.append(fib(n)) return seq
咦，这两个append好像可以合并：
def fib_seq(n): seq = [] if n > 0: seq.extend(fib_seq(n-1)) seq.append(fib(n)) return seq
哇，原来如此！
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
