IBM SPSS Modeler算法系列-----决策树CHAID算法
在之前的微信文章中，有一篇名为《 SPSS Modeler决策树算法比较 》的文章，粗略介绍了 SPSS Modeler 中各种决策树算法（包括C5.0、CHAID、QUEST、C&R和决策列表）的区别，这可以帮助大家在选用算法的时候有一些参考。
谈到算法，大家都觉得挺神秘的，对没有学过统计学相关知识的朋友来说，太多的数学公式没法理解，很多书籍介绍的也比较表象，看得云里雾里的，那么今天，我们将尝试给大家介绍SPSS Modeler里面所涵盖的一些算法内容，既不那么地表象，也不那么地难以理解。
我们首先从决策树算法开始，先介绍CHAID算法， 它是由Kass在1975年提出的，全称是Chi-squaredAutomatic Interaction Detector，可以翻译为卡方自动交叉检验，从名称可以看出，它的核心是卡方检验，那么我们先来了解下什么是卡方检验。
卡方检验只针对分类变量，它是统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，卡方值越大，偏离程度越大；卡方值越小，偏差越小，若两个值完全相等时，卡方值就为0，表明理论值完全符合。
在CHAID算法中，我们可以结合下面这个例子来理解卡方检验上面这段话。
这个例子中，我们要分析的目标是女性考虑结婚与不结婚的问题（0表示不结婚，1表示结婚），那么影响结婚不结婚的因素有很多，比如男方有没有房子，男方收入水平， 幸福指数等等。那么我们先来看看到底是否有房对是否结婚是否有影响。
首先，我们对数据做下统计：
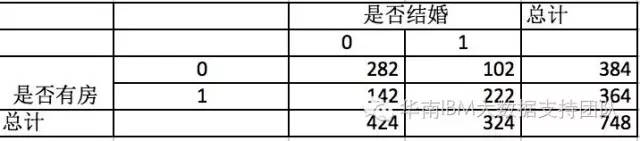
我们先假设是否有房与结婚没有关系，那么四个格子应该是括号里的数（理论值），这和实际值（括号外的数）是有差距的，理论和实际的差距说明原假设不成立。
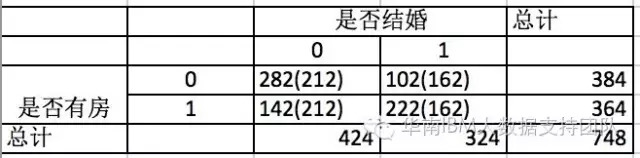
那么这个差距怎么来评判呢？我们就用到卡方的计算公式：
K方的计算公式可以这么描述， 这四个格子里，每个格子的（实际值-理论值）^2/理论值，即K^2 ==（282-212）^2/212+(102-162) ^2/162+(142-212) ^2/212+(222-162) ^2/162=90.6708，然后我们再去查卡方表，可以看到，自由度为1，显著性水平为0.05的卡方临界值为3.84。计算得到的卡方值大于3.84，也就是说，原假设成立的概率小于0.05,即5%，所以我们拒绝原假设，可以得到是否有房对结婚是有影响的。从卡方的计算方法中，可以看到卡方越大，实际值与理论值差异越大，两者没有关系的原假设就越不成立。
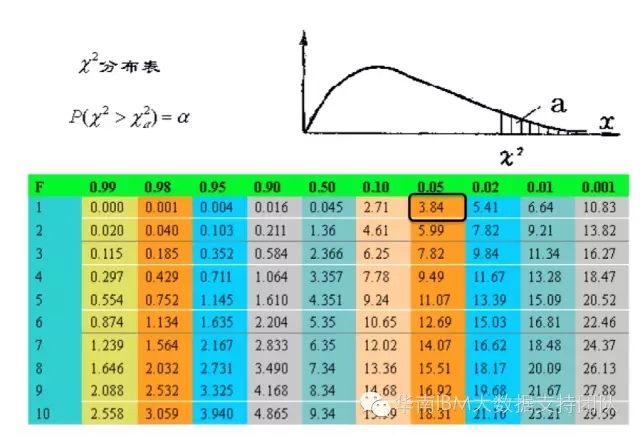
那么以上就是对卡方检验在分析两者关系的介绍。
接下来我们回到CHAID算法，我们在IBM SPSS Modeler构建这个模型，得到的决策树结果如下（部分截图）：
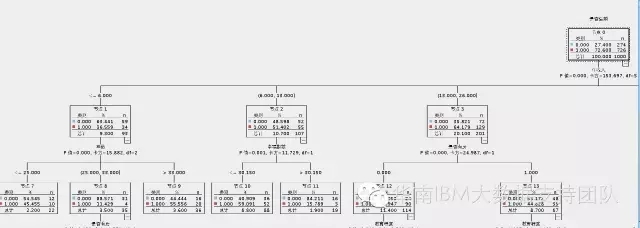
很多人看到这个图的时候，一般会有两个疑惑，第一个，影响的第一个最重要的因素是年收入，那么年收入区间的划分为什么是 [<=6.000]、[6.000，13.000]……这个以6.0、13.0等为临界划分点，是预先设定好的吗？当然不是，这是CHAID这个算法的计算逻辑决定的。第二个疑惑是，为什么会以年收入作为第一个分割点，而不是其它呢？
我们先来看第一个问题，划分的临界点是怎么确定的，这个问题，其实是该算法中，对数据预处理的部分。 需要注意的是, 卡方检验只针对分类变量，而CHAID算法，是支持数值变量和分类变量的，所以，首先算法的第一步，就是对输入变量做预处理，分两种情况，输入变量是数值型或者是分类型，先来介绍输入变量是数值型的情况，比如我们例子中的年收入就是数值型的，那么，需要先将其离散化成为字符型，也就是划分区间，这里采用的是ChiMerge分组法，这个接下来会结合这个例子的年收入指标来介绍下这个分组法。
- Step1:对年收入值从小到大进行排序1、2、3、4…….
- Step2:定义若干初始区间，使输入变量的每个变量值均单独落入一个区间内，像这里的收入都是整数，所以会以1作为组限，分为[1]、[2]、[3]、[4]……等各个区间；
- Step3:计算每个切分好的年收入值的频次，得到输入变量与输出变量的交叉分组频数表。
- Step4:计算两两相临组的卡方值。根据显著性水平和自由度得到卡方临界值。如果卡方值小于临界值，说明输入变量在该相邻区间上的划分，对输出变量取值没有显著影响，可以合并;
这里的Step3和Step4，我们这么来理解，输入变量是年收入，我们已经把它划分为[1]、[2]……,那么在下面这个表中，我们先计算了年收入第一位和第二位分别为1和2的人数（即Step3中的频次计算），得到下面这个交叉表：
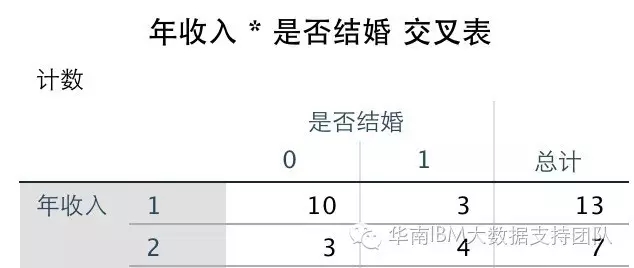
然后开始计算卡方值，卡方值的计算公式为： K^2 = n (ad - bc) ^ 2 / [(a+b)(c+d)(a+c)(b+d)] 其中a、b、c、d分别对应的值如下图：（其中n=a+b+c+d为样本容量）。
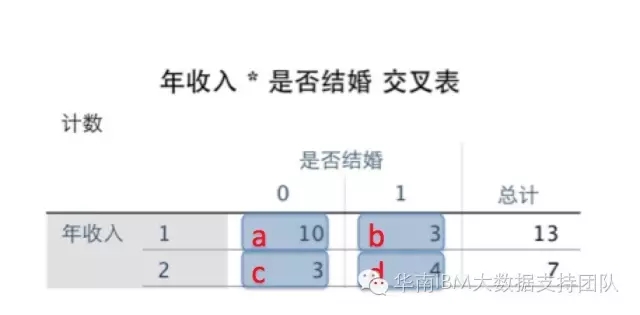
因此计算得到的卡方值=（10+3+3+4）*（10*4-3*3）^2/[(10+3)(3+4)(10+3)(3+4)]=2.321
细心的朋友可能会发现，这个计算公式跟我们上面计算的公式写法有点不一样，其实是经过公式变形的，上面是为了更好地理解卡方的含义，下面这个公式是变形后，比较好记的公式。
这个时候，我们查看卡方表如下图：
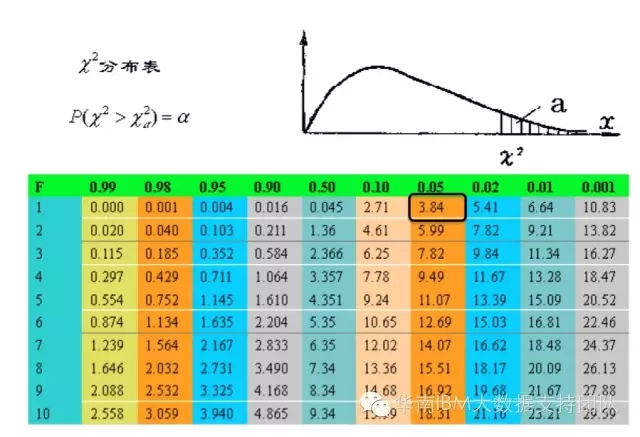
可以看到，自由度为1，显著性水平为0.05的卡方临界值为3.84，我们计算得到的卡方2.321小于3.84，说明年收入为1或者2，对结婚或者不结婚没有显著影响，因此可以合并，所以会将收入为[1]、[2]合并为[1,2]；接下来计算[3]、[4]的卡方，依次类推。
PS:这里选择的显著性水平为0.05是可以自己设置更改的，在SPSS Modeler的CHAID算法中可以自己设置，如下图位置：
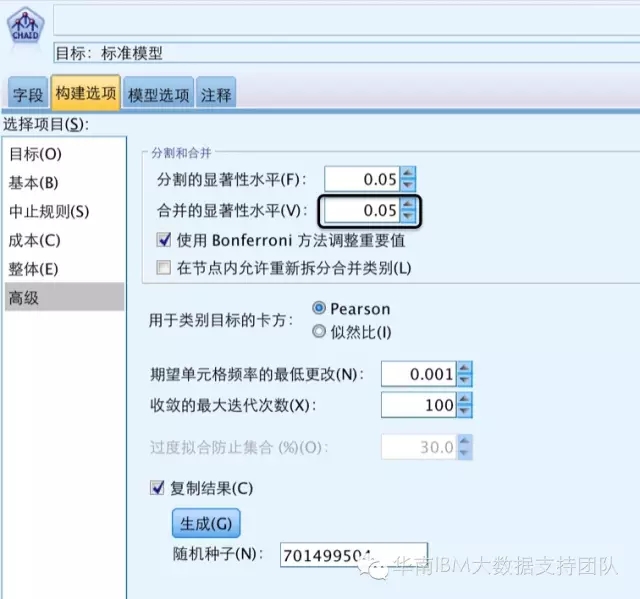
Step5:重复Step3至Step4,直到任何两个相临组无法合并，即卡方值都不小于临界值为止。
那么如果输入变量是分类型的，与上面的数值型对比，就少了一次对数值离散化的过程，直接对分类变量中的元素进行卡方检验及合并，最终形成“超类”，直至输入变量的“超类”无法再合并为止。对于顺序型分类输入变量，只能合并相邻的类别。
对数据完成预处理之后，就要选择根节点，也就是计算输出变量（是否结婚）与输入变量相关性检验的统计量的概率P-值，即卡方值对应的P-值，P-值越小，说明输入变量与输出变量的关系越紧密，应当作为当前最佳分组变量。当P-值相同时，应该选择检验统计量观测值最大的输入变量，也就是卡方最大的输入变量。
在上面的决策树图中，我们可以看到，每个指标都有计算好的卡方值和P-值，从分析结果中，也可以验证上面所说的，P-值越小，越在树的顶端，P-值相同时，卡方越大，越在树的顶端。
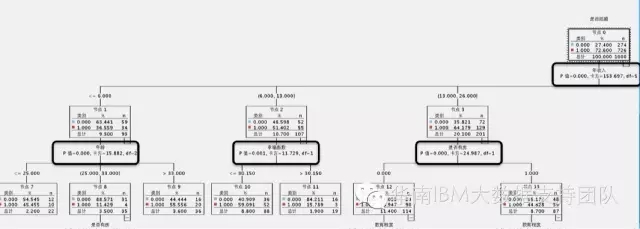
到这里，就解答了一开始查看决策树时候的两个疑惑。
我们这个例子里面呢，目标变量是否结婚，是分类型的变量，那么，如果目标变量是数值型的呢？那么在第一步的数据预处理的时候，把采用的卡方值计算改为方差计算，在第二步选择最佳分割点的时候，使用的是方差分析计算得到F统计量的P-值，而不是卡方的P-值。
这里以Income这个连续变量作为输出变量（即目标）为例，得到的决策树，对应的值就是P值以及F统计量，如下图：
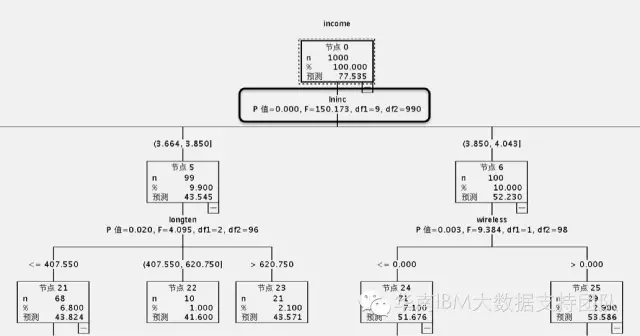
针对这个算法，有以下几个特点总结下：
- 样本数据必须足够大，要求样本含量应大于40且每个格子中的理论频数不应小于5。当样本含量大于40但有1=<理论频数<5时，卡方值需要校正，当样本含量小于40或理论频数小于1时只能用确切概率法计算概率。
- 目标变量可以是分类型，也可以是数值型；
- 输入变量可以是分类型，也可以是数值型。
- 在IBM SPSS Modeler里面，针对 CHAID算法，以上介绍的内容是大概的计算框架，里面其实还开放出了许多参数可以影响这个树的生长，比如不用Pearson 卡方，而是似然比卡方；使用交互树生长模型来影响树的生长；中止树生长的规则等等。
SPSS Modeler 试用版下载地址: http://bigdata.evget.com/product/168.html
更多大数据与分析相关行业资讯、解决方案、案例、教程等请点击查看>>>
详情请咨询 在线客服 ！
客服热线：023-66090381
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
