转载

C语言中的有符号和无符号的理解

就像我们必须决定某个量使用整数还是实数，使用多大的范围数一样，我们必须自已决定某个量是否需要正负。如果这个量不会有负值，那么我们可以定它为带正负的类型。

在计算机中，可以区分正负的类型，称为有符类型（signed），无正负的类型（只有正值），称为无符类型。（unsigned）数值类型分为整型或实型，其中整型又分为无符类型或有符类型，而实型则只有符类型。字符类型也分为有符和无符类型。比如有两个量，年龄和库存，我们可以定前者为无符的字符类型，后者定为有符的整数类型。

2.使用二制数中的最高位表示正负:

首先得知道最高位是哪一位？1个字节的类型，如字符类型，最高位是第7位，2个字节的数，最高位是第15位，4个字节的数，最高位是第31位。不同长度的数值类型，其最高位也就不同，但总是最左边的那位（如下示意）。字符类型固定是1个字节，所以最高位总是第7位。

(红色为最高位)

单字节数：

11111111

双字节数：

11111111 11111111

四字节数：

11111111 11111111 11111111 11111111

当我们指定一个数量是无符号类型时，那么其最高位的1或0，和其它位一样，用来表示该数的大小。

当我们指定一个数量是无符号类型时，此时，最高数称为“符号位”。为1时，表示该数为负值，为0时表示为正值。

#### 3.无符号数和有符号数的范围区别:

无符号数中，所有的位都用于直接表示该值的大小。有符号数中最高位用于表示正负，所以，当为正值时，该数的最大值就会变小。我们举一个字节的数值对比：

无符号数：11111111 值：255

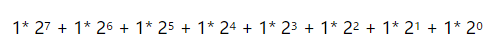
有符号数：01111111 值：127

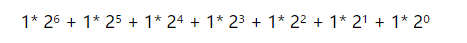
eg：（本屌实在不知道怎么用md语法来打出数学公式，2的幂次方）

同样是一个字节，无符号数的最大值是255，而有符号数的最大值是127。原因是有符号数中的最高位被挪去表示符号了。并且，我们知道，最高位的权值也是最高的（对于1字节数来说是2的7次方=128），所以仅仅少于一位，最大值一下子减半。

不过，有符号数的长处是它可以表示负数。因此，虽然它的在最大值缩水了，却在负值的方向出现了伸展。我们仍一个字节的数值对比：

无符号数：0 —————– 255

有符号数：-128 ——— 0 ———- 127

同样是一个字节，无符号的最小值是 0 ，而有符号数的最小值是-128。

所以二者能表达的不同的数值的个数都一样是256个。只不过前者表达的是0到255这256个数，后者表达的

是-128到+127这256个数。

一个有符号的数据类型的最小值是如何计算出来的呢？

有符号的数据类型的最大值的计算方法完全和无符号一样，只不过它少了一个最高位（见第3点）。但在负值

范围内，数值的计算方法不能直接使用1 26 + 1 25 的公式进行转换。

在计算机中，负数除为最高位为1以外，还采用补码形式进行表达。所以在计算其值前，需要对补码进行还原。这里，先直观地看一眼补码的形式：

在10进制中：1 表示正1，而加上负号：-1 表示和1相对的负值。

那么，我们会很容易认为在2进制中（1个字节）： 0000 0001 表示正1，则高位为1后：1000 0001应该表示-1。

然而，事实上计算机中的规定有些相反，请看下表：

|二进制（1字节）| 十进制值 |

|:——: | —— |

|10000000 | -128 |

|10000001 | -127 |

|10000010 | -126 |

|10000011 | -125 |

|10000100 | -124 |

| …… | …… |

|11111110 | -2 |

|11111111 | -1 |

首先我们看到，从-1到-128，其二进制的最高位都是1，正如我们前面说的，负数最高位为1，然后我们觉得有点奇怪了，1000 0000 并没有用来表示 0；而 1000 0001也不是拿来直观地表示-1，事实上，-1用1111 1111来表示。

怎么理解这个问题呢？先问一句是-1大还是-128大？

当然是-1大，那么，1111 1111 -1是什么呢？和现实中的计算结果完全一致。1111 1111 -1=1111 1110，而1111 1110 就是-2，就这样一直减下去，当见到只剩最高位用于表示符号的1意外，其他低位全为0时，就是最小的负值，在一字节中，最小的负值是1000 0000，也就是-128。

我们以-1位例，来看看不同字节数的整数中，如何表达-1这个数；

| 字节数 | 二进制值 | 十进制值 |

| :——: | —— | —— |

|单字节数 | 11111111 | -1 |

|双字节数 | 11111111 11111111 |-1 |

| 四字节数| 11111111 11111111 11111111 11111111 | -1 |

可能有些人看到这里，就已经混了，为什么呢？1111 1111 有时表示255，有时又表示-1？所以我再强调前面说的第二点，你自己决定一个数是有符号还是无符号的，写程序时，指定一个量是有符号的，那么当这个量的二进制各位上的数都是1时，它表示的数就是-1；相反，如果事先声明这个量是无符号的，此时它表示的就是该量允许的最大值，对于一个字节的数来说，最大值就是255。

我们已经知道计算机中，所有数据最终都是使用二进制数表达。也已经学会如何将一个10进制数如何转换为二进制数。不过，我们仍然没有学习一个负数如何用二进制表达。比如，假设有一 int 类型的数，值为5，那么，我们知道它在计算机中表示为：

5转换成二制是101，不过int类型的数占用4字节（32位），所以前面填了一堆0。现在想知道，-5在计算机中如何表示？在计算机中，负数以其正值的补码形式表达。什么叫补码呢？这得从原码，反码说起。

原码：一个整数，按照绝对值大小转换成的二进制数，最高为为符号位，称为原码。红色为符号位

比如：

00000000 00000000 00000000 00000101  是 5的原码。                                                  10000000 00000000 00000000 00000101  是-5的原码

反码：将二进制除符号位数按位取反，所得的新二进制数称为原二进制数的反码。正数的反码为原码，负数的反码是原码符号位外按位取反。

取反操作指：原为1，得0；原为0，得1。（1变0; 0变1）

正数：正数的反码与原码相同。负数：负数的反码，符号位为“1”，数值部分按位取反。

比如：将10000000 00000000 00000000 00000101除符号位每一位取反，

得11111111 11111111 11111111 11111010。

这时候我们称：11111111 11111111 11111111 11111010 是 10000000 00000000 00000000 00000101 的反码。

反码是相互的，所以也可称：

11111111 11111111 11111111 11111010 和 10000000 00000000 00000000 00000101 互为反码。

补码：反码加1称为补码。（如果反码最后一位是1得话就向前加1）

1. 正数：正数的补码和原码相同。

2. 负数：按照规则来

也就是说，要得到一个数的补码，先得到反码，然后将反码加上1，所得数称为补码。

11111111 11111111 11111111 11111010 是 10000000 00000000 00000000 00000101（-5）的反码。

加1得11111111 11111111 11111111 11111011

所以，-5 在计算机中表达为：11111111 11111111 11111111 11111011。转换为十六

进制：0xFFFFFFFB。

再举一例，我们来看整数-1在计算机中如何表示。

假设这也是一个int类型，那么：

1、先取-1的原码： 10000000 00000000 00000000 00000001

2、除符号位取反得反码：11111111 11111111 11111111 11111110

3、加1得补码： 11111111 11111111 11111111 11111111 可见，－1在计算机里用二进制表达就是全1。16进制为：0xFFFFFF。

#### 计算机中带有符号数用补码表示的优点：

1、负数的补码与对应正数的补码之间的转换可以用同一种方法——求补运算完成，可以简化硬件；

2、可将减法变为加法，省去减法器；

3、无符号数及带符号数的加法运算可以用同一电路完成。

可得出一种心算求补的方法——从最低位开始至找到的第一个1均不变，符号位不变，这之间的各位“求反”(该方法仅用于做题）

方法	例子1	列子2
1,从右边开始，找到第一个“1”	10101001	10101100
2,从这个“1”之后开始到最左边取反（不包括符号位，也就是最高位）	11010111	11010100