转载

二叉树的先序遍历

二叉树

基本定义简单如下：

二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。

先序遍历

首先访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根结点，然后遍历左子树，最后遍历右子树，如果二叉树为空则返回。

                                R
                           /         /
                          A          B
                      /     /      /     /
                    C      D     E       F

上面这个树的先序遍历顺序是：R A C D B E F

遍历的实现

递归实现
简单迭代实现
优化迭代实现

基础 Tree 定义

public class Tree {
	private Tree left;
	private Tree right;
	private String data;

	public Tree(Tree left, Tree right, String data) {
		super();
		this.left = left;
		this.right = right;
		this.data = data;
	}

	public Tree getLeft() {
		return left;
	}

	public void setLeft(Tree left) {
		this.left = left;
	}

	public Tree getRight() {
		return right;
	}

	public void setRight(Tree right) {
		this.right = right;
	}

	public String getData() {
		return data;
	}

	public void setData(String data) {
		this.data = data;
	}

}

递归实现

public class PreTraverse1 {
	public static Tree init() {
		Tree E = new Tree(null, null, "E");
		Tree F = new Tree(null, null, "F");
		Tree C = new Tree(null, null, "C");
		Tree D = new Tree(null, null, "D");
		Tree A = new Tree(C, D, "A");
		Tree B = new Tree(E, F, "B");

		Tree root = new Tree(A, B, "R");

		return root;
	}

	public static void main(String[] args) {
		Tree root = init();
		traverse(root);
	}

	private static void traverse(Tree root) {
		if (root == null) {
			return;
		}
        //如果当前传入的节点是null，那么不进行处理
        //第一步：先访问根节点，这里以输出代替
        //第二步：递归访问左子树
        //第三步：递归访问右子树
		System.out.print(root.getData() + " ");
		traverse(root.getLeft());
		traverse(root.getRight());
	}

}

迭代实现

import java.util.Stack;

public class PreTraverse2 {
	public static Tree init() {
		Tree E = new Tree(null, null, "E");
		Tree F = new Tree(null, null, "F");
		Tree C = new Tree(null, null, "C");
		Tree D = new Tree(null, null, "D");
		Tree A = new Tree(C, D, "A");
		Tree B = new Tree(E, F, "B");

		Tree root = new Tree(A, B, "R");

		return root;
	}

	public static void main(String[] args) {
		Tree root = init();
		traverse(root);
	}

	private static void traverse(Tree root) {
		Stack<Tree> stack = new Stack<>();
		stack.push(root);
		//利用了栈的先进后出的特性，先把root入栈
		while (!stack.isEmpty()) {//循环判断栈不是空
			Tree popTree = stack.pop();//把栈顶的元素弹出
			System.out.print(popTree.getData() + " ");//1. 访问元素
			if (popTree.getRight() != null) {
				stack.push(popTree.getRight());//2. 如果右节点不为空，push 到栈中，因为是先进后出，所以先 push 右节点
			}
			if (popTree.getLeft() != null) {
				stack.push(popTree.getLeft());//3. push 左节点
			}
		}
	}
}

优化迭代实现

如下图所示：

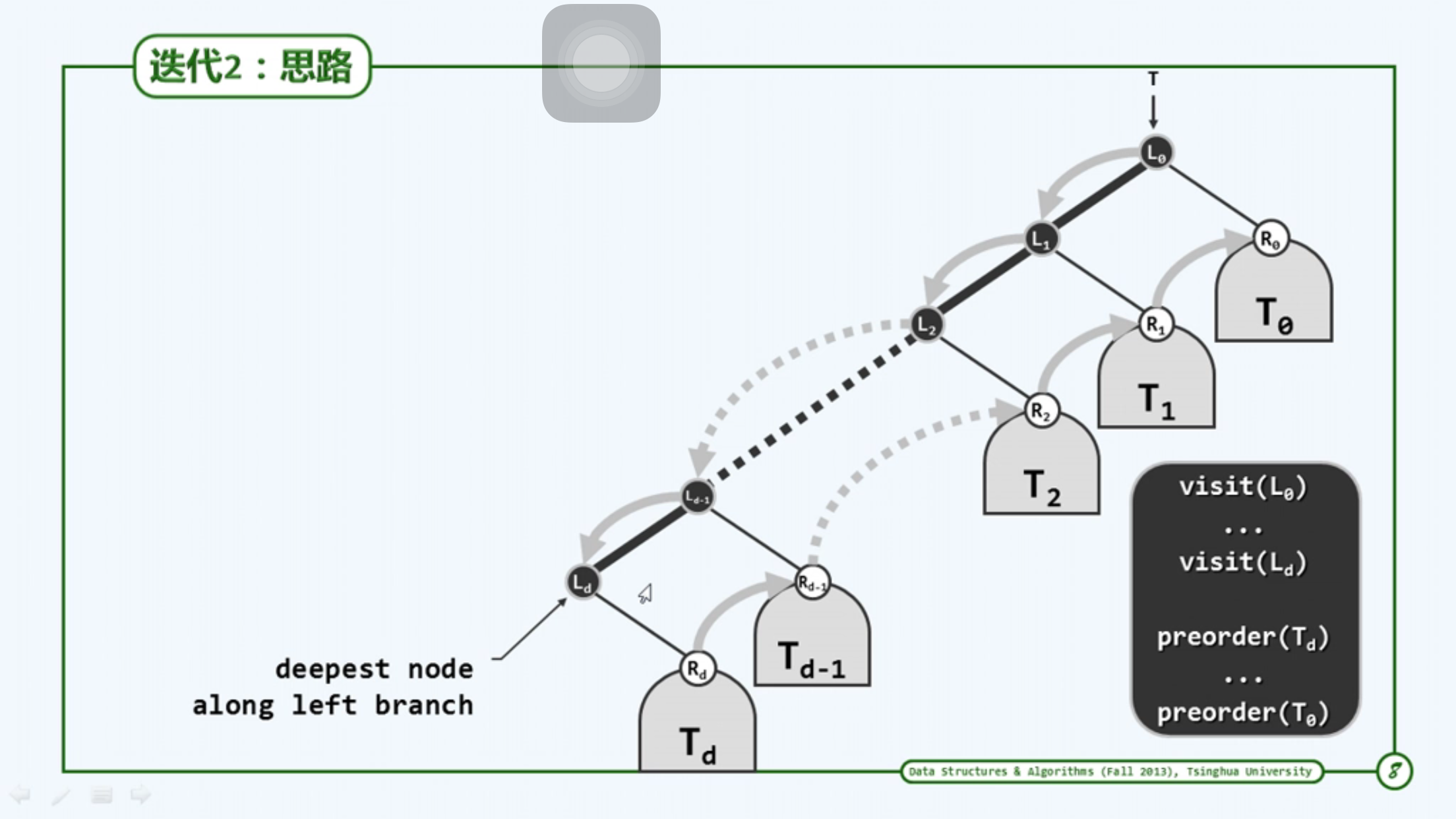
二叉树的先序遍历

import java.util.Stack;

public class PreTraverse {

	public static Tree init() {
		Tree E = new Tree(null, null, "E");
		Tree F = new Tree(null, null, "F");
		Tree C = new Tree(null, null, "C");
		Tree D = new Tree(null, null, "D");
		Tree A = new Tree(C, D, "A");
		Tree B = new Tree(E, F, "B");

		Tree root = new Tree(A, B, "R");

		return root;
	}

	public static void main(String[] args) {
		Tree root = init();
		traverse(root);
	}

	public static void traverse(Tree root) {
		Stack<Tree> stack = new Stack<>();
		while (true) {
			visitAlongLeftBranch(root, stack);
			if (stack.isEmpty()) {
				break;
			}
            //当最左节点已经访问完，弹出栈顶元素(也就是距离当前最近的右子树)，然后循环这个过程，直到栈是空退出
			root = stack.pop();
		}
	}

     //遍历的过程可看成如下：
     //先访问当前根节点
     //然后把右节点 push 到栈
     //在循环当前节点的左节点
	private static void visitAlongLeftBranch(Tree root, Stack<Tree> stack) {
		while (root != null) {
			System.out.print(root.getData() + " ");
			stack.push(root.getRight());
			root = root.getLeft();
		}
	}
}