二叉树的基本概念和实现
继续是《数据结构算法与应用:C++语言描述》的笔记,这是第八章二叉树和其他树的内容,本节内容介绍树的定义以及二叉树的代码实现。
树
树t是一个非空的有限元素的集合,其中一个元素为根,余下的元素组成t的子树。
在画一棵树时,每个元素都代表一个节点。树根在上面,其子树画在下面。如下图所示,其中,Ann,Mary,John是Joe的 孩子(children) ,而Joe是他们的 父母(parent) 。有相同父母的孩子是 兄弟(sibling) 。Ann,Mary,John都是兄弟。此外,还有其他术语: 孙子(grandchild),祖父(grandparent),祖先(ancestor),后代(descendent)等 。树中没有孩子的元素称为 叶子(leaf) 。图中Ann,Mark,Sue和Chris是树的叶子。
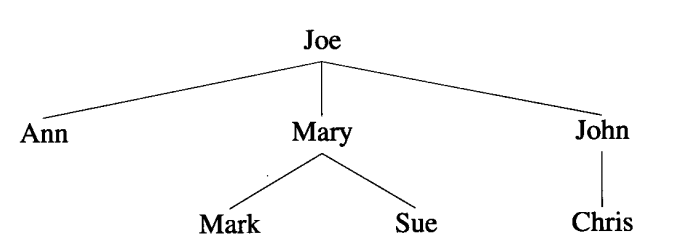
树的另一个常用术语是 级(level) 。指定树根的级是1,其孩子的级是2,依次类推。上图中Joe的级是1,而Ann,Mary,John的级是2,然后Mark,Sue,Chris的级是3。
元素的度是指其孩子的个数。叶节点的度是0。 树的度是其元素度的最大值 。所以上图中的度是3。
二叉树
定义:二叉树(binary tree)t是有限个元素的集合(可以为空)。当二叉树非空时,其中有一个称为根的元素,余下的元素(如果有的话)被组成2个二叉树,分别称为t的左子树和右子树。
二叉树和树的根本区别是:
- 二叉树可以为空,树不能为空
- 二叉树中每个元素都恰好有两棵子树(其中一个或两个可能为空)。而树中每个元素可以有若干子树。
- 在二叉树中每个元素的子树都是有序的,也就是说,可以用左、右子树来区别。而树的子树间是无序的。
下图给出了表示数学表达式的二叉树,总共有3个数学表达式。每个操作符可以有一个或两个操作数,左操作数是操作符的左子树,而右操作数则是右子树。树中的叶节点是常量或者变量。
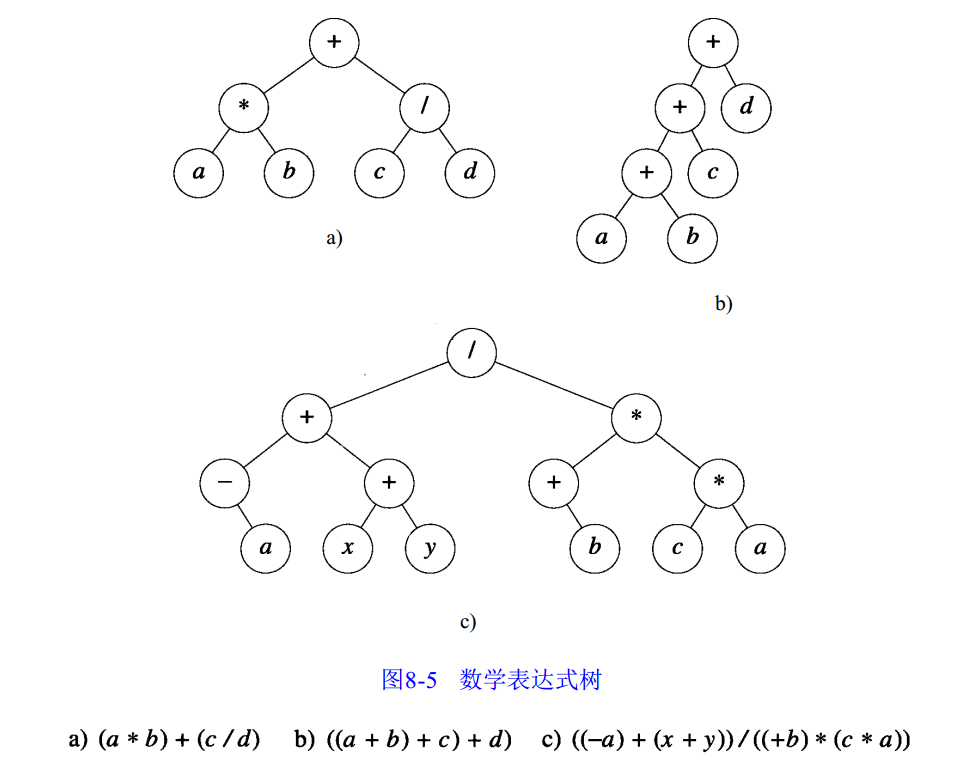
二叉树的特性
特性1: 包含n(n>0)个元素的二叉树边数是n-1。
证明 二叉树中每个元素 (除了根节点)有且只有一个父节点。在子节点与父节点间有且只有一条边,因此边数为n-1。
二叉树的高度或者深度是指该二叉树的层数。
特性2: 若二叉树的高度为h,$h /ge 0$,则该二叉树最少有h个元素,最多有$2^h - 1$个元素。
证明 因为每一层最少要有1个元素,因此元素数最少为h。每元素最多有2个子节点,则第i层节点元素最多为$2^i-1$个,i>0。h=0时,元素的总数为0,也就是$2^0-1$。当h>0时,元素的总数不会超过$/sum_{i=1}^h 2^{i-1}=2^h-1$。
特性3: 包含n个元素的二叉树的高度最大是n,最小是$/left/lceil log_2(n+1) /right/rceil$。
证明 因为每层至少有一个元素,因此高度不会超过n。由特性2,可以得知高度为h的二叉树最多有$2^h-1$个元素。因为$n /le 2^h-1$,因此$h /ge log_2(n+1)$。由于h是整数,所以$h /ge /left/lceil log_2(n+1) /right/rceil$。
当高度是h的二叉树恰好有$2^h - 1$个元素时,称其为满二叉树(full binary tree)。下图就是一个高度为4的满二叉树。
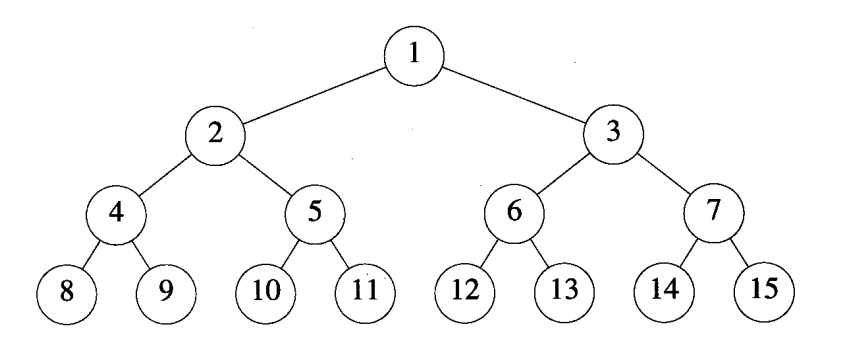
假设对高度为h的满二叉树中的元素从上到下,从左到右的顺序进行从1到$2^h - 1$进行编号,如上图所示。假设从满二叉树中删除k个元素,其编号为$2^h - i, 1 /le i /le k$,所得到的二叉树称为 完全二叉树(complete binary tree) 。如下图给出的三棵完全二叉树。注意, 满二叉树是完全二叉树的一个特例,并且有n个元素的完全二叉树的深度是$/left/lceil log_2(n+1) /right/rceil$ 。
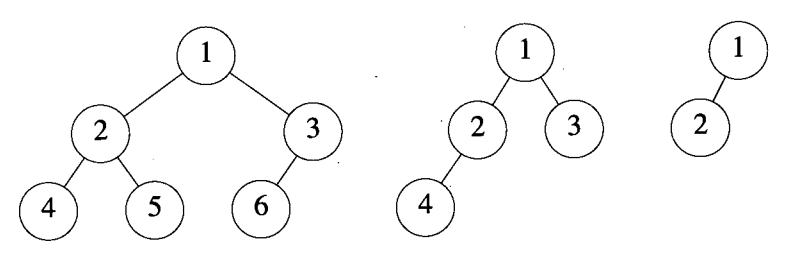
在完全二叉树中,一个元素与其孩子的编号有非常好的对应关系。其关系在下面特性4中给出。
特性4: 设完全二叉树中一元素的序号是i,$1 /le i /le n$。则有以下关系成立:
1) 当i=1时,该元素为二叉树的根,若i>1,则该元素父节点的编号是$/left/lfloor i/2 /right/rfloor$。
2) 当2i>n时,该元素没有左子树,否则,其左子树的编号是2i。
3) 若2i+1>n时,该元素没有右子树,否则,其右子树的编号是2i+1。
二叉树描述
公式化描述
二叉树的公式化描述利用特性4。二叉树可以作为缺少了部分元素的完全二叉树。下图给出了二叉树的两个例子。
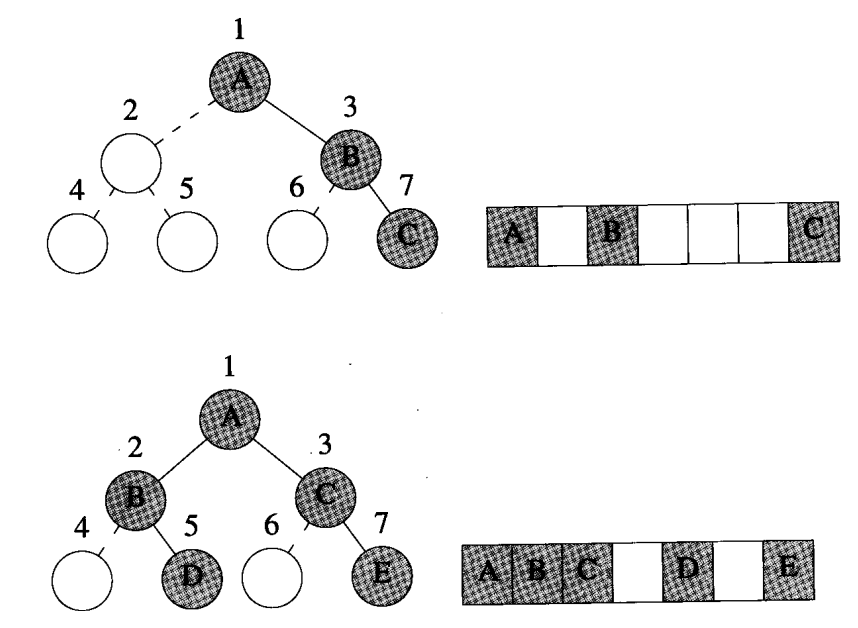
在公式化描述方法中,按照二叉树对元素的编号方法,将二叉树的元素存储在数组中。上图同时给出了二叉树的公式化描述,即图中右侧的数组表示。
当缺少很多元素时,这种描述方法非常浪费空间。实际上,一个有n个元素的二叉树可能最多需要$2^n-1$的空间来存储。当每个节点都是其他节点的右孩子时,存储空间达到最大。如下图所示的一棵有四个元素的二叉树,这种类型的二叉树称为右斜二叉树。当缺少的元素比较少时,这种描述方法很有效。
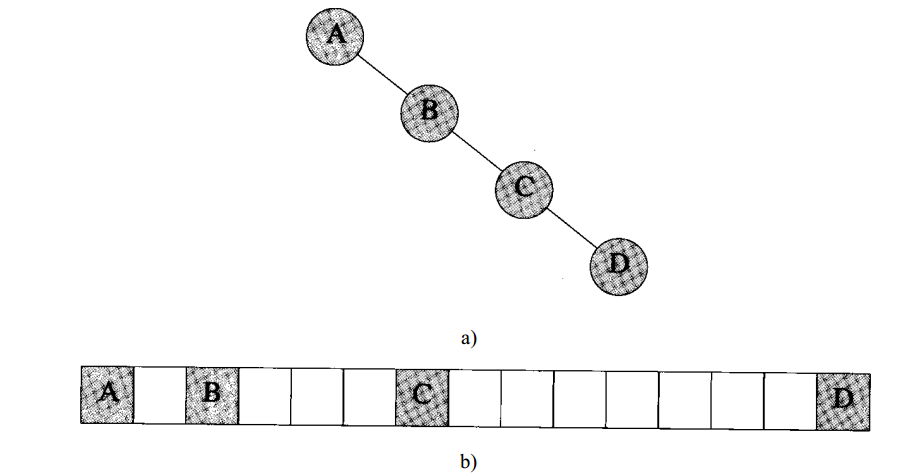
链表描述
二叉树最常用的描述方法是用链表或指针。每个元素都用一个有两个指针域的节点表示,这两个域是 LeftChild和RightChild 。除此两个指针域外,每个节点还有一个data域。其代码实现如下所示。
template<class T> class BinaryTreeNode{ friend void Visit(BinaryTreeNode<T> *); friend void InOrder(BinaryTreeNode<T> *); friend void PreOrder(BinaryTreeNode<T> *); friend void PostOrder(BinaryTreeNode<T> *); friend void LevelOrder(BinaryTreeNode<T> *); friend void main(void); private: T data; BinaryTreeNode<T>* LeftChild, *RightChild; public: BinaryTreeNode(){ LeftChild = RightChild = 0; } BinaryTreeNode(const T& e){ data = e; LeftChild = RightChild = 0; } BinaryTreeNode(const T&e, BinaryTreeNode *l, BinaryTreeNode* r){ data = e; LeftChild = l; RightChild = r; } };
二叉树的边可以用一个从父节点到子节点的指针来描述。指针放在父节点的指针域中,因为包括n个元素的二叉树恰有n-1条边,所以有 2n-(n-1)=n+1 个指针域没有值,这些域被值为0。下图给出了公式化描述中第一幅图的二叉树的链表描述。
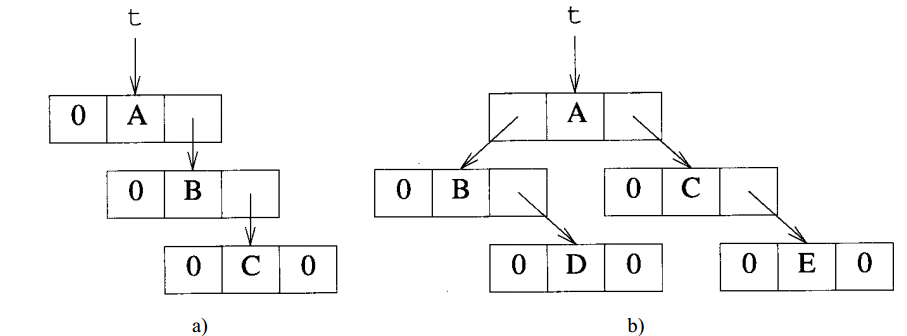
二叉树中不设置指向父节点的指针一般不会有什么问题,因为在二叉树的大部分函数中并不需要此指针。
二叉树遍历
有四种遍历二叉树的方法:
- 前序遍历
- 中序遍历
- 后序遍历
- 逐层遍历
前3种遍历方法将在下面给出代码实现。
template<class T> void PreOrder(BinaryTreeNode<T>* t){ if (t){ // 访问根节点 Visit(t); // 前序遍历左子树 PreOrder(t->LeftChild); // 前序遍历右子树 PreOrder(t->RightChild); } } template<class T> void InOrder(BinaryTreeNode<T>* t){ if (t){ // 中序遍历左子树 InOrder(t->LeftChild); Visit(t); InOrder(t->RightChild); } } template<class T> void PostOrder(BinaryTreeNode<T>* t){ if (t){ // 后序遍历左子树 PostOrder(t->LeftChild); PostOrder(t->RightChild); Visit(t); } }
这三种方法,每个节点的左子树都在其右子树之前遍历。 这三种遍历的区别在于对同一个节点在不同时刻进行访问。 在进行前序遍历时,每个节点是在其左右子树被访问之前进行访问的;在中序遍历时,首先访问左子树,然后访问子树的根节点,最后访问右子树。在后序遍历时,当左右子树均访问完之后才访问子树的根节点。
下图给出上述三种方法对前文给出的数学表达式分别产生的结果,其中 Visit(t) 由 cout<< t->data; 代替。

当对一棵数学表达式树进行前、中、后序遍历时,便分别得到表达式的前缀、中缀和后缀表达式。中缀(infix)形式就是平时书写的数学表达式。使用中缀形式的时候由于没有括号,可能会产生一些歧义,比如对于 x+y*z ,可以理解为 (x+y)*z 或者 x+(y*z) ,为了避免这种歧义,可以使用完全括号化的中缀表达式,每个操作符和相应的操作数都用一对括号括起来。下面是改进后的中序遍历算法的代码:
template<class T> void Infix(BinaryTreeNode<T> *t){ // 输出完全括号的中缀表达式 if (t){ cout << "("; // 左操作数 Infix(t->LeftChild); // 操作符 cout << t->data; // 右操作数 Infix(t->RightChild); cout << ")"; } }
在后缀(postfix)表达式中,每个操作符跟在操作数之后,操作数从左到右的顺序出现;在前缀(prefix)表达式中,操作符位于操作数之前。前缀和后缀表达式都不会存在歧义,不需要采用括号或者优先级。从左到右或者从右到左扫描表达式并采用操作数栈,可以很容易确定操作数和操作符的关系。若在扫描中遇到一个操作数,把它压入堆栈,遇到一个操作符,则将其与栈顶的操作数相匹配,把这些操作数推出栈,由操作符执行相应的计算,并将所得结果作为操作数压入堆栈。
逐层遍历就是 按从顶层到底层的次序访问树中元素,在同一层中,从左到右进行访问。 由于遍历中使用的是一个队列而不是栈,因此写一个按层遍历的递归程序很困难。下列程序是采用队列来实现对二叉树进行逐层遍历,队列中的元素指向二叉树节点,这里使用了之前队列章节中使用的类 LinkedQueue 。
template<class T> void LevelOrder(BinaryTreeNode<T>* t){ // 对*t逐层遍历 LinkedQueue<BinaryTreeNode<T>*> Q; while (t){ Visit(t); // 将t的右孩子放入队列 if (t->LeftChild) Q.Add(t->LeftChild); if (t->RightChild) Q.Add(t->RightChild); // 访问下一个节点 try{ Q.Delete(t); } catch (OutOfBounds){ return; } } }
上述程序中,首先仅当树非空时,才进入 while 循环。首先访问根节点,然后将其子节点加到队列中。当队列添加操作失败时,由Add会引发 NoMem 异常,由于没有捕捉该异常,所以发生该异常时函数将退出。在添加操作成功后,就进行从队列中删除t元素,如果成功,则删除的元素会返回到t中,这个删除的元素也就是下一个要访问的节点。下次访问该节点的时候,又会将其左右子树加入到队列的尾部,然后下一个要访问的就是根节点的右子树(如果存在),如此就可以实现逐层遍历了。而如果删除失败就表明队列为空,也就是意味着遍历的结束。
假设二叉树中元素的数目是 n 。这四种遍历算法的空间复杂性均为$O(n)$,时间复杂性是$/theta(n)$。当t的高度是n的时候,通过观察期前序、中序和后序遍历时所使用的递归栈空间可得到上述结论。当t是满二叉树的时候,逐层遍历所需要的队列空间是$/theta(n)$。每个遍历算法花在树中每个节点上的时间是$/theta(1)$(假设访问一个节点的时间是$/theta(1)$)。
抽象数据类型BinaryTree
下面给出二叉树的抽象数据类型,这里只列出几个常用的操作:
抽象数据类型 BinaryTree{ 实例 元素集合;如果不空,则被划分为根节点、左子树和右子树; 每个子树仍是一个二叉树 操作 Create():创建一个空的二叉树; IsEmpty:如果二叉树为空,则返回 true ,否则返回false Root(x):取x为根节点;如果操作失败,则返回false,否则返回true MakeTree(root,left,right):创建一个二叉树,root作为根节点,left作为左子树, right作为右子树 BreakTree(root,left,right):拆分二叉树 PreOrder:前序遍历 InOrder:中序遍历 PostOrder:后序遍历 LevelOrder:逐层遍历 }
类BinaryTree
下面给出类 BinaryTree 的C++定义。函数 Visit 作为遍历函数的参数,以实现不同操作的实现。该定义中使用了链表描述的二叉树。
template<class T> class BinaryTree{ private: BinaryTreeNode<T> *root; // 根节点指针 void PreOrder(void(*Visit)(BinaryTreeNode<T>*u), BinaryTreeNode<T>* t); void Inorder(void(*Visit)(BinaryTreeNode<T>*u), BinaryTreeNode<T>* t); void PostOrder(void(*Visit)(BinaryTreeNode<T>*u), BinaryTreeNode<T>* t); public: BinaryTree(){ root = 0; } ~BinaryTree(){}; bool IsEmpty() const{ return ((root) ? false : true); } bool Root(T& x)const; void MakeTree(const T& element, BinaryTree<T>& left, BinaryTree<T>& right); void BreakTree(const T& element, BinaryTree<T>& left, BinaryTree<T>& right); void PreOrder(void(*Visit)(BinaryTreeNode<T>*u)){ PreOrder(Visit, root); } void Inorder(void(*Visit)(BinaryTreeNode<T>*u)){ Inorder(Visit, root); } void PostOrder(void(*Visit)(BinaryTreeNode<T>*u)){ PostOrder(Visit, root); } void LevelOrder(void(*Visit)(BinaryTreeNode<T>*u)); };
下面会给出共享成员函数 Root,MakeTree,BreakTree 的代码。函数 MakeTree 和 BreakTree 要求参与操作的三棵树应该互不相同,否则程序会得出错误的结果。
template<class T> bool BinaryTree<T>::Root(T& x)const{ // 取根节点的data域,放入x,如果没有则返回false if (root){ x = root->data; return true; } else return false; } template<class T> void BinaryTree<T>::MakeTree(const T& element, BinaryTree<T>& left, BinaryTree<T>& right){ // 将left,right和element合并成一棵新树,并且要求left和right及this必须是不同的树。 // 创建新树 root = new BinaryTreeNode<T>(element, left.root, right.root); // 阻止访问left和right left.root = right.root = 0; } template<class T> void BinaryTree<T>::BreakTree(T& element, BinaryTree<T>& left, BinaryTree<T>& right){ // left,right 和this必须是不同的树 if (!root) // 空树 throw BadInput(); // 分解树 element = root->data; left.root = root->LeftChild; right.root = root->RightChild; delete root; root = 0; }
下面给出四种遍历方法的实现代码。
template<class T> void BinaryTree<T>::PreOrder(void(*Visit)(BinaryTreeNode<T>*u), BinaryTreeNode<T>* t){ // 前序遍历 if (t){ Visit(t); PreOrder(Visit, t->LeftChild); PreOrder(Visit, t->RightChild); } } template<class T> void BinaryTree<T>::Inorder(void(*Visit)(BinaryTreeNode<T>*u), BinaryTreeNode<T>* t){ // 中序遍历 if (t){ Inorder(Visit, t->LeftChild); Visit(t); Inorder(Visit, t->RightChild); } } template<class T> void BinaryTree<T>::PostOrder(void(*Visit)(BinaryTreeNode<T>*u), BinaryTreeNode<T>* t){ // 后序遍历 if (t){ PostOrder(Visit, t->LeftChild); PostOrder(Visit, t->RightChild); Visit(t); } } template<class T> void BinaryTree<T>::LevelOrder(void(*Visit)(BinaryTreeNode<T>* u)){ // 逐层遍历 LinkedQueue<BinaryTreeNode<T>*>Q; BinaryTreeNode<T> *t; t = root; while (t){ Visit(t); // 将t的右孩子放入队列 if (t->LeftChild) Q.Add(t->LeftChild); if (t->RightChild) Q.Add(t->RightChild); // 访问下一个节点 try{ Q.Delete(t); } catch (OutOfBounds){ return; } } }
接下来是对类BinaryTree的简单应用,程序中构造了一个四节点的二叉树,并进行了前序遍历以确定书中的节点数目。
#include<iostream> #include"xcept.h" #include"BinaryTree.h" using std::cout; using std::endl; using std::cin; int count = 0; BinaryTree<int>a, x, y, z; template<class T> void ct(BinaryTreeNode<T>* t){ count++; } void main(void){ y.MakeTree(1, a, a); z.MakeTree(2, a, a); x.MakeTree(3, y, z); y.MakeTree(4, x, a); y.PreOrder(ct); cout <<"Tree y has "<< count <<" nodes"<< endl; system("pause"); return; }
抽象数据类型及类的扩充
本节将扩充之前给出的抽象数据类型,增加如下二叉树操作:
- PreOutput(): 按前序方式输出数据域
- InOutput(): 按中序方式输出数据域
- PostOutput(): 按后序方式输出数据域
- LevelOutput(): 逐层输出数据域
- Delete(): 删除一棵二叉树,释放其节点
- Height(): 返回树的高度
- Size(): 返回树中节点数
输出
四个输出函数可以通过定义一个私有静态成员函数Output来实现,该函数代码如下:
static void Output(BinaryTreeNode<T>*t){ cout << t->data << ", "; }
而四个共享输出函数的形式如下:
void PreOutput(){ PreOrder(Output, root); cout << endl; } void InOutput(){ Inorder(Output, root); cout << endl; } void PostOutput(){ PostOrder(Output, root); cout << endl; } void PreOutput(){ LevelOrder(Output); cout << endl; }
由于Visit操作的时间复杂性是$/theta(1)$,对包括n个节点的二叉树来说,每种遍历方法所花费的时间是$/theta(n)$(遍历成功的话),因此每种输出方法的时间复杂性均为$/theta(n)$。
删除
要删除一棵二叉树,需要删除其所有节点,可以通过 后序遍历 在访问一个节点时,将其删除,也就是先删除左子树,然后右子树,最后删除根。因此函数 Delete 的形式如下所示:
void Delete(){ PostOrder(Free, root); root = 0; } static void Free(BinaryTreeNode<T>* t){ delete t; }
其中函数 Free 是一个私有成员函数。要删除的二叉树有n个节点时, Delete 函数的时间复杂性是$/theta(n)$。
计算高度
通过进行后序遍历,可以得到二叉树的高度。首先得到左子树的高度hl,然后得到右子树的高度hr,则树的高度为 max{hl,hr}+1 。
但是这里不能使用之前定义的后序遍历代码,因为在进行遍历的时候需要有返回值(也就是子树的高度)。所以首先需要在增加一个共享成员函数Height,其代码为:
int Height() const{ return Height(root); }
然后增加一个私有成员函数 Height ,其实现如下:
template<class T> int BinaryTree<T>::Height(BinaryTreeNode<T> *t)const{ // 返回树*t的高度 if (!t) return 0; // 左子树高度 int hl = Height(t->LeftChild); // 右子树的高度 int hr = Height(t->RightChild); if (hl > hr) return ++hl; else return ++hr; }
上述函数的时间复杂性是$/theta(n)$。
统计节点数
可以用上述四种遍历方法中的任何一种来获取二叉树中的节点数,因为每种遍历方法都对每个节点仅访问一次,只要在访问每个节点的时候将一个全局计数器加1即可。所以首先在类 BinaryTree 定义外定义一个全局变量: int _count; ,然后增加一个共享成员函数 Size 和私有成员函数 Add1 ,其代码实现如下:
static void Add1(BinaryTreeNode<T>* t){ _count++; } int Size(){ _count = 0; PreOrder(Add1, root); return _count; }
函数 Size 的时间复杂性是$/theta(n)$。
对于类 BinaryTree 的定义以及测试例子可以查看 二叉树
小结
本节内容主要是介绍了树的基本概念以及二叉树的定义、特性和实现代码,包括四种遍历树的方法。











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

