转载

AABB包围盒算法,在2D碰撞检测中的实现

一：介绍

碰撞检测是游戏开发中常用到的基础功能,通常的物理引擎中都会包含碰撞引擎.我们今天主要介绍

的就是Dynamic AABB Tree的实现原理,AABB Tree是个二叉树,从名字上看,像是个动态平衡树的变种。

确实在构造AABB树的时候是需要balance逻辑的。但是AABB的平衡不是基于数的深度的而是"面积",后面

会详细介绍。

为了方便介绍,后文里的将用ABT来代表AABB Tree

二：引言

AABB包围盒算法,在2D碰撞检测中的实现

这个游戏想必大家都玩过,这里面就牵扯到一个碰撞检测的问题,需要实时检测用户控制的小车是否

碰到了障碍物,最简单的方法就是枚举每一个障碍物,判断障碍物是否跟用户控制的小车有交集。

当障碍物少的时候,比如障碍物有100～10000个的时候枚举是可以解决的,但是在一些加有物理引

擎的场景里,枚举就显然行不通了,因为需要判断每一个物体是否被其它n-1个物体碰撞。如果我们还是用

枚举的形式来做碰撞检测那么时间复杂度就是n!,如果有100个物体,那么做一次检测的时间复杂度就已经

难以接受。

在枚举算法做碰撞检测的时候有存在一个很大的问题,那就是如果两个物体距离很远,远到它们不可能

接触,但是检测中还是会枚举这对组合。

ABT是基于二叉树实现的,这时候我们能大概感觉到,它的时间复杂度将会从枚举的n*n变成nlog(n)

接下来我们看下具体原理

三：碰撞体的预处理

为什么预处理？我们看下面的两个图。如果我们需要对这两张图片做碰撞检测,该如何处理？

AABB包围盒算法,在2D碰撞检测中的实现

我们可以基于像素的对比,判断青蛙的像素坐标有没有出现在钥匙的像素坐标里,如果有重叠的部分

那说明,两个物体碰撞里,但是仔细想一下这并不是很好的办法,假如我们两个照片都是600*600像素,那么

单单这两个物体的碰撞检测的时间复杂度就是600^4。

很显然不能这么做,我么接下来对图片进行"描边"。我们就会得到两个矩形。那么接下来就好处理了。

二：ABT树的构建过程

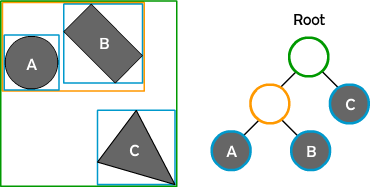
AABB包围盒算法,在2D碰撞检测中的实现

假设上图中的A,B,C是我们要做碰撞检测的物体,外面的蓝色框体就是我们对物体描边以后获得的矩形

接下来就是构建树的过程,上面说过ABT树中的每一个节点是AABB Tree结构。我们从左至右建树,就像构建

二叉排序树一样。

step-1: 把A加入到树结构中,作为根节点
step-2: 把B加入到数结构中,这时需要和根节点做比较,判断根节点的区域是否跟B有交集,如果有的话
        就判断子节点是否跟B有交集,如果都没有就判断B分别加入子节点区域后的面积,找到面节差最
        小的,组合。如果B与根节点没有交集,就把A和B当作一个整体重新构建轮廓(橘黄色的矩形),并
        生成A,B的父节点(上图中橘黄色的圆圈),
step-3: 把C加入到树中,判断是否有交集,方法与step-2中一样,最终得到上图中的树

最终所有的物体将会在树的叶节点上。
树中除叶节点外,所有的节点存的都是自己的面积,或是说是自己的轮廓矩形的四个点的坐标。这样的话,一旦

判断一个对象是否与树中物体碰撞,我们只需判断是否与物体所在区域有交集,如果有就说明"有可能"会碰撞,然后

接着递归向下,直到找到与目标物体碰撞的叶节点。

整个过程中,很想是一个二叉排序树,给一个数字,判断这个数字在不在二叉排序树中。

无论是二叉排序树也好还是ABT算法也好,最重要的还是它们都巧妙的使用里二分法,不要ABT算法的二分法是将

面积进行二分,尽可能的避免搜索错误区域。

所以ABT算法在检测一个物体是否与其它物体碰撞的时候时间负责度是log(n)的(n为碰撞物体的数量)。

原文 https://segmentfault.com/a/1190000006802081

正文到此结束