数据结构：图的表示

任何一本讲到图算法的算法书，都会讲到图的表示方法有两种

1 邻接矩阵 ，对于N个点的图，需要N×N的矩阵表示点与点之间是否有边的存在。这种表示法的缺点是浪费空间，尤其是对于N×N的矩阵是稀疏矩阵，即边的数目远远小于N×N的时候，浪费了巨大的存储空间

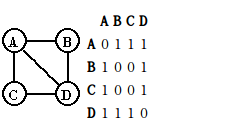
2 邻接链表，对于任何一个node A，外挂一个邻接链表，如果存在 A->X这样的边，就将X链入链表。 这种表示方法的优点是节省空间，缺点是所有链表都存在的缺点，地址空间的不连续造成缓存命中降低，性能有不如临界矩阵这样的数组。

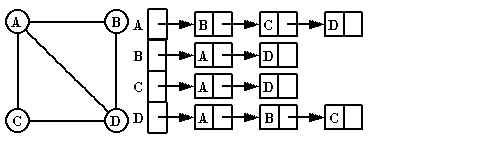
一直以来，我也是觉得，鱼和熊掌不可兼得，这是无可奈何的事情。直到我看到了一份比较完美的code。他有动态分配的数组来存放邻接节点。一起欣赏下这份代码吧。年前我第一次看到这份代码的时候，激动的我晚上半天睡不着觉。平时自己写的代码，一板一眼，虽说功能无误，总少了那么几分灵气。看了C算法，也算对图的表示方法知道一些，却写不出这么优美的代码。

我以前觉得，自己大量练习联系写代码是学习编程的最好的方法，是最开但是看了这份代码后，觉得，学习前辈高人优秀的代码，是提高自己的一条捷径，对我们这些普通的coder而言，我们看代码的时间是超过写代码的时间的。阅读前辈优秀代码，会更快的提升自己的编程能力。对于初学者尤其是这样，这也是进入一个优秀的开发team的重要性，能更快的成长。

欣赏代码Yale大学前辈的代码吧。

#ifndef __GRAPH_H__
#define __GRAPH_H__
 
typedef struct graph *Graph;
 
Graph graph_create(int n);
void graph_destroy(Graph);
void graph_add_edge(Graph, int source, int sink);
int graph_vertex_count(Graph);
int graph_edge_count(Graph);
int graph_out_degree(Graph, int source);
int graph_has_edge(Graph, int source, int sink);
void graph_foreach(Graph g, int source,
        void (*f)(Graph g, int source, int sink, void *data),
        void *data);
 
#endif

#include <stdlib.h>
#include <assert.h>
 
#include "graph.h"
 
/* basic directed graph type */
/* the implementation uses adjacency lists
* represented as variable-length arrays */
 
/* these arrays may or may not be sorted: if one gets long enough
* and you call graph_has_edge on its source, it will be */
 
struct graph {
    int n;                                             /* number of vertices */
    int m;                                             /* number of edges */
    struct successors {
        int d;                                         /* number of successors */
        int len;                                       /* number of slots in array */
        char is_sorted;                                /* true if list is already sorted */
        int list[1];                                  
                                                       /* actual list of successors */
    } *alist[1];
};
 
/* create a new graph with n vertices labeled 0..n-1 and no edges */
Graph
graph_create(int n)
{
    Graph g;
    int i;
 
    g = malloc(sizeof(struct graph) + sizeof(struct successors *) * (n-1));
    assert(g);
 
    g->n = n;
    g->m = 0;
 
    for(i = 0; i < n; i++) {
        g->alist[i] = malloc(sizeof(struct successors));
        assert(g->alist[i]);
 
        g->alist[i]->d = 0;
        g->alist[i]->len = 1;
        g->alist[i]->is_sorted= 1;
    }
    
    return g;
}
 
/* free all space used by graph */
void
graph_destroy(Graph g)
{
    int i;
 
    for(i = 0; i < g->n; i++) free(g->alist[i]);
    free(g);
}
 
/* add an edge to an existing graph */
void
graph_add_edge(Graph g, int u, int v)
{
    assert(u >= 0);
    assert(u < g->n);
    assert(v >= 0);
    assert(v < g->n);
 
    /* do we need to grow the list? */
    while(g->alist[u]->d >= g->alist[u]->len) {
        g->alist[u]->len *= 2;
        g->alist[u] =
            realloc(g->alist[u],
                sizeof(struct successors) + sizeof(int) * (g->alist[u]->len - 1));
    }
 
    /* now add the new sink */
    g->alist[u]->list[g->alist[u]->d++] = v;
    g->alist[u]->is_sorted = 0;
 
    /* bump edge count */
    g->m++;
}
 
/* return the number of vertices in the graph */
int
graph_vertex_count(Graph g)
{
    return g->n;
}
 
/* return the number of vertices in the graph */
int
graph_edge_count(Graph g)
{
    return g->m;
}
 
/* return the out-degree of a vertex */
int
graph_out_degree(Graph g, int source)
{
    assert(source >= 0);
    assert(source < g->n);
 
    return g->alist[source]->d;
}
 
/* when we are willing to call bsearch */
#define BSEARCH_THRESHOLD (10)
 
static int
intcmp(const void *a, const void *b)
{
    return *((const int *) a) - *((const int *) b);
}
 
/* return 1 if edge (source, sink) exists), 0 otherwise */
int
graph_has_edge(Graph g, int source, int sink)
{
    int i;
 
    assert(source >= 0);
    assert(source < g->n);
    assert(sink >= 0);
    assert(sink < g->n);
 
    if(graph_out_degree(g, source) >= BSEARCH_THRESHOLD) {
        /* make sure it is sorted */
        if(! g->alist[source]->is_sorted) {
            qsort(g->alist[source]->list,
                    g->alist[source]->d,
                    sizeof(int),
                    intcmp);
        }
        
        /* call bsearch to do binary search for us */
        return
            bsearch(&sink,
                    g->alist[source]->list,
                    g->alist[source]->d,
                    sizeof(int),
                    intcmp)
            != 0;
    } else {
        /* just do a simple linear search */
        /* we could call lfind for this, but why bother? */
        for(i = 0; i < g->alist[source]->d; i++) {
            if(g->alist[source]->list[i] == sink) return 1;
        }
        /* else */
        return 0;
    }
}
 
/* invoke f on all edges (u,v) with source u */
/* supplying data as final parameter to f */
void
graph_foreach(Graph g, int source,
    void (*f)(Graph g, int source, int sink, void *data),
    void *data)
{
    int i;
 
    assert(source >= 0);
    assert(source < g->n);
 
    for(i = 0; i < g->alist[source]->d; i++) {
        f(g, source, g->alist[source]->list[i], data);
    }
}

这是一份 PineWiki 网站里面提供的一份图的表示的代码，实现的很优美吧？动态分配数组，长度可以扩展，既不浪费空间，有不会带来性能损失。

除此外，graph_foreach这种思想也很不错啊。最近学习了一段时间的Lisp，这种传递函数作用到每一个元素上的方法，相当于Lisp中的mapcar，让人不仅拍案叫绝，很容易就能扩展出很好的功能。（当然也不是完全没瑕疵，比如realloc没有判断失败的情景，白璧微瑕）

既然是图的表示，我们当然很希望能够看到可视化的图。我看Land of Lisp一书中，学到了Linux下的neato 命令。 Linux下有工具帮助生成图的图片，可以满足我们可视化的需求。

先看下测试代码。

#include <stdio.h>
#include <assert.h>
 
#include "graph.h"
 
#define TEST_SIZE (6)
 
static void
match_sink(Graph g, int source, int sink, void *data)
{
    assert(data && sink == *((int *) data));
}
 
static int node2dot(Graph g)
{
    assert(g != NULL);
    return 0;
}
 
static void print_edge2dot(Graph g,int source, int sink, void *data)
{
    fprintf(stdout,"%d->%d;n",source,sink);
}
static int edge2dot(Graph g)
{
    assert( NULL);
    int idx = 0;
    int node_cnt = graph_vertex_count(g);
    for(idx = 0;idx<node_cnt; idx++)
    {
        graph_foreach(g,idx,print_edge2dot,NULL);
    }
    return 0;
}
 
int graph2dot(Graph g)
{
    fprintf(stdout,"digraph{");
    node2dot(g);
    edge2dot(g);
    fprintf(stdout,"}n");
    return 0;
}
 
int main(int argc, char **argv)
{
    Graph g;
    int i;
    int j;
 
    g = graph_create(TEST_SIZE);
 
    assert(graph_vertex_count(g) == TEST_SIZE);
 
    /* check it's empty */
    for(i = 0; i < TEST_SIZE; i++) {
        for(j = 0; j < TEST_SIZE; j++) {
            assert(graph_has_edge(g, i, j) == 0);
        }
    }
 
    /* check it's empty again */
    for(i = 0; i < TEST_SIZE; i++) {
        assert(graph_out_degree(g, i) == 0);
        graph_foreach(g, i, match_sink, 0);
    }
 
    /* check edge count */
    assert(graph_edge_count(g) == 0);
 
    for(i = 0; i < TEST_SIZE; i++) {
        for(j = 0; j < TEST_SIZE; j++) {
            if(i < j) graph_add_edge(g, i, j);
        }
    }
 
 
    for(i = 0; i < TEST_SIZE; i++) {
        for(j = 0; j < TEST_SIZE; j++) {
            assert(graph_has_edge(g, i, j) == (i < j));
        }
    }
     assert(graph_edge_count(g) == (TEST_SIZE*(TEST_SIZE-1)/2));
    graph2dot(g);
    /* free it
     * */
    graph_destroy(g);
 
    return 0;
}

我们这个测试程序基本测试了graph的API，同时利用graph_foreach函数的高效扩展性，输出了dot文件格式的文件我们看下执行结果。

root@manu:~/code/c/self/graph_2# gcc -o test generate_graph.c graph.c
root@manu:~/code/c/self/graph_2# ./test >test.dot

在我的Ubuntu下面用XDot可以看到test.dot已经是个图形文件了。图形如下：

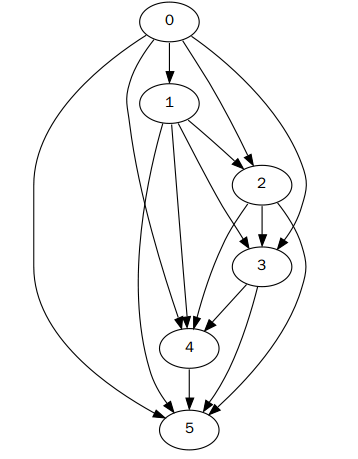
当然了，我们也可以用 dot命令绘制出PNG格式的图片来：

root@manu:~/code/c/self/graph_2# dot -T png -o graph_test.png test.dot

我们可以看到在当前目录下产生了一个文件名为graph_test.png的PNG格式的图片。打开看下和上面的图是一致的。我就不贴图了。

对dot感兴趣的筒子，可以继续阅读 『dot 学习笔记』二. 记录 Shell 的变迁

参考文献：

1  Land of Lisp

2   PineWiki

3 算法：C语言实现。