转载

BloomFilter原理，实现及优化

最近在做性能优化相关的事情，其中涉及到了BloomFilter，于是对BloomFilter总结了下，本文组织结构如下：

BloomFilter的使用场景
BloomFilter的原理
BloomFilter的实现及优化

BloomFilter的使用场景

首先，简单来看下BloomFilter是做什么的？

A Bloom filter is a space-efficient probabilistic data structure, conceived by Burton Howard Bloom in 1970, that is used to test whether an element is a member of a set. False positive matches are possible, but false negatives are not, thus a Bloom filter has a 100% recall rate. In other words, a query returns either “possibly in set” or “definitely not in set”.

上述描述引自维基百科，特点总结为如下：

空间效率高的概率型数据结构，用来检查一个元素是否在一个集合中
对于一个元素检测是否存在的调用，BloomFilter会告诉调用者两个结果之一：可能存在或者一定不存在

其次，为什么需要BloomFilter？

常用的数据结构，如hashmap，set，bit array都能用来测试一个元素是否存在于一个集合中，相对于这些数据结构，BloomFilter有什么方面的优势呢？

对于hashmap，其本质上是一个指针数组，一个指针的开销是sizeof(void *)，在64bit的系统上是64个bit，如果采用开链法处理冲突的话，又需要额外的指针开销，而对于BloomFilter来讲，返回可能存在的情况中，如果允许有1%的错误率的话，每个元素大约需要10bit的存储空间，整个存储空间的开销大约是hashmap的15%左右（数据来自维基百科）
对于set，如果采用hashmap方式实现，情况同上；如果采用平衡树方式实现，一个节点需要一个指针存储数据的位置，两个指针指向其子节点，因此开销相对于hashmap来讲是更多的
对于bit array，对于某个元素是否存在，先对元素做hash，取模定位到具体的bit，如果该bit为1，则返回元素存在，如果该bit为0，则返回此元素不存在。可以看出，在返回元素存在的时候，也是会有误判的，如果要获得和BloomFilter相同的误判率，则需要比BloomFilter更大的存储空间

当然，BloomFilter也有它的劣势，如下：

相对于hashmap和set，BloomFilter在返回元素可能存在的情况中，有一定的误判率，这时候，调用者在误判的时候，会做一些不必要的工作，而对于hashmap和set，不会存在误判情况
对于bit array，BloomFilter在插入和查找元素是否存在时，需要做多次hash，而bit array只需要做一次hash，实际上，bit array可以看做是BloomFilter的一种特殊情况

最后，以一个例子具体描述使用BloomFilter的场景，以及在此场景下，BloomFilter的优势和劣势。

一组元素存在于磁盘中，数据量特别大，应用程序希望在元素不存在的时候尽量不读磁盘，此时，可以在内存中构建这些磁盘数据的BloomFilter，对于一次读数据的情况，分为以下几种情况：

请求的元素不在磁盘中，如果BloomFilter返回不存在，那么应用不需要走读盘逻辑，假设此概率为P1；如果BloomFilter返回可能存在，那么属于误判情况，假设此概率为P2
请求的元素在磁盘中，BloomFilter返回存在，假设此概率为P3

如果使用hashmap或者set的数据结构，情况如下：

请求的数据不在磁盘中，应用不走读盘逻辑，此概率为P1+P2
请求的元素在磁盘中，应用走读盘逻辑，此概率为P3

假设应用不读盘逻辑的开销为C1，走读盘逻辑的开销为C2，那么，BloomFilter和hashmap的开销为

Cost(BloomFilter) = P1 * C1 + (P2 + P3) * C2
Cost(HashMap) = (P1 + P2) * C1 + P3 * C2;

Delta = Cost(BloomFilter) - Cost(HashMap)
      = P2 * (C2 - C1)

因此，BloomFilter相当于以增加 P2 * (C2 - C1) 的时间开销，来获得相对于hashmap而言更少的空间开销。

既然P2是影响BloomFilter性能开销的主要因素，那么BloomFilter设计时如何降低概率P2（即false positive probability）呢？，接下来的BloomFilter的原理将回答这个问题。

BloomFilter的原理

原理

BloomFilter通常采用bit array实现，假设其bit总数为m，初始化时m个bit都被置成0。

BloomFilter中插入一个元素，会使用k个hash函数，来计算出k个在bit array中的位置，然后，将bit array中这些位置的bit都置为1。

以一个例子，来说明添加的过程，这里，假设m=19，k=2，如下：

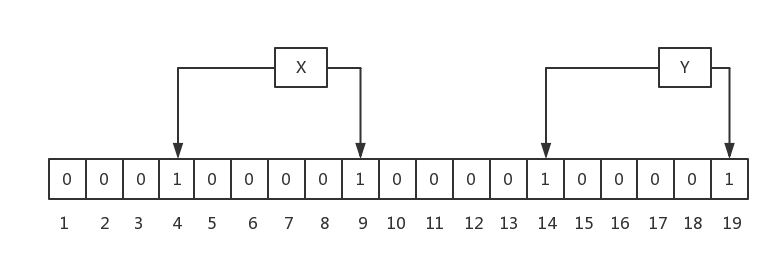
BloomFilter原理，实现及优化

如上图，插入了两个元素，X和Y，X的两次hash取模后的值分别为4,9，因此，4和9位被置成1；Y的两次hash取模后的值分别为14和19，因此，14和19位被置成1。

BloomFilter中查找一个元素，会使用和插入过程中相同的k个hash函数，取模后，取出每个bit对应的值，如果所有bit都为1，则返回元素可能存在，否则，返回元素不存在。

为什么bit全部为1时，是表示元素可能存在呢？

还是以上图的例子说明，如果要查找的元素是X，k个hash函数计算后，取出的bit都是1，此时，X本身也是存在的；假如，要查找另一个元素Z，其hash计算出来的位置为9,14，此时，BloomFilter认为此元素存在，但是，Z实际上是不存在的，此现象称为false positive。

最后，BloomFilter中不允许有删除操作，因为删除后，可能会造成原来存在的元素返回不存在，这个是不允许的，还是以一个例子说明：

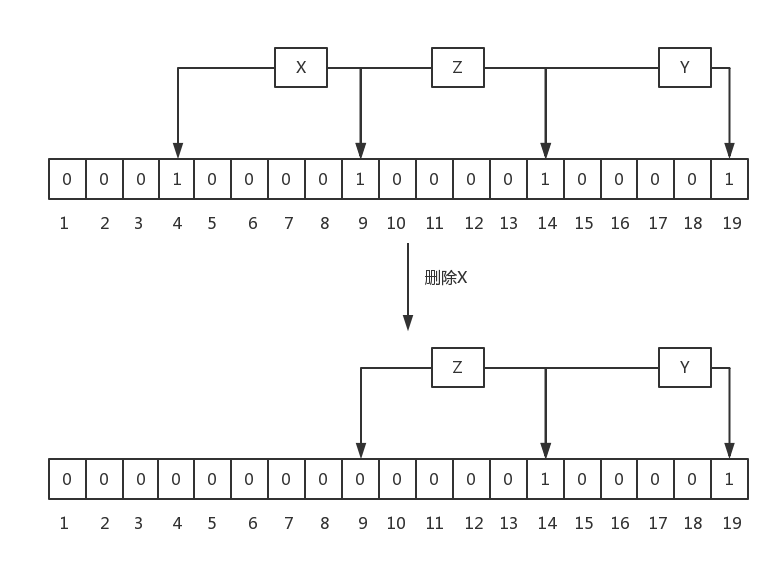
BloomFilter原理，实现及优化

上图中，刚开始时，有元素X，Y和Z，其hash的bit如图中所示，当删除X后，会把bit 4和9置成0，这同时会造成查询Z时，报不存在的问题，这对于BloomFilter来讲是不能容忍的，因为它要么返回绝对不存在，要么返回可能存在。

放到之前的磁盘读数据的例子来讲，如果删除了元素X，导致应用读取Z时也会返回记录不存在，这是不符合预期的。

BloomFilter中不允许删除的机制会导致其中的无效元素可能会越来越多，即实际已经在磁盘删除中的元素，但在bloomfilter中还认为可能存在，这会造成越来越多的false positive，在实际使用中，一般会废弃原来的BloomFilter，重新构建一个新的BloomFilter。

参数如何取值

在实际使用BloomFilter时，一般会关注false positive probability，因为这和额外开销相关。实际的使用中，期望能给定一个false positive probability和将要插入的元素数量，能计算出分配多少的存储空间较合适。

假设BloomFilter中元素总bit数量为m，插入的元素个数为n，hash函数的个数为k，false positive probability记做p，它们之间有如下关系（具体推导过程请参考维基百科）：

如果需要最小化false positive probability，则k的取值如下

k = m * ln2 / n;  公式一

而p的取值，和m，n又有如下关系

m = - n * lnp / (ln2) ^ 2 公式二

把公式一代入公式二，得出给定n和p，k的取值应该为

k = -lnp / ln2

最后，也同样可以计算出m。

BloomFilter实现及优化

基本版实现

基础的数据结构如下：

template<typename T>
class BloomFilter
{
 public:
  BloomFilter(const int32_t n, const double false_positive_p);
  void insert(const T &key);
  bool key_may_match(const T &key);
 
 private:
  std::vector<char> bits_;
  int32_t k_; 
  int32_t m_; 
  int32_t n_; 
  double p_; 
};

其中bits_是用vector 模拟的bit array，其他对应于BloomFilter原理一节所说的几个参数。

整个BloomFilter包含三个操作：

初始化：即上述代码中的构造函数
插入：即上述代码中的insert
判断是否存在：即上述代码中的key_may_match

初始化

根据BloomFilter原理一节中的方法进行计算，代码如下：

template<typename T>
BloomFilter<T>::BloomFilter(const int32_t n, const double false_positive_p)
  : bits_(), k_(0), m_(0), n_(n), p_(false_positive_p)
{
  k_ = static_cast<int32_t>(-std::log(p_) / std::log(2));
  m_ = static_cast<int32_t>(k_ * n * 1.0 / std::log(2));
  bits_.resize((m_ + 7) / 8, 0); 
}

这里开始实现的时候犯了个低级的错误，一开始用的是 bits_.reserve ，导致BloomFilter的false positive probability非常高，原因是reserve方法只分配内存，并不进行初始化。

插入

即设置每个hash函数计算出来的bit为1，代码如下

template<typename T>
void BloomFilter<T>::insert(const T &key)
{
  uint32_t hash_val = 0xbc9f1d34;
  for (int i = 0; i < k_; ++i) {
    hash_val = key.hash(hash_val);
    const uint32_t bit_pos = hash_val % m_;
    bits_[bit_pos/8] |= 1 << (bit_pos % 8);
  }
}

判断是否存在

即计算每个hash函数对应的bit的值，如果全为1，则返回存在；否则，返回不存在。

template<typename T>
bool BloomFilter<T>::key_may_match(const T &key)
{
  uint32_t hash_val = 0xbc9f1d34;
  for (int i = 0; i < k_; ++i) {
    hash_val = key.hash(hash_val);
    const uint32_t bit_pos = hash_val % m_;
    if ((bits_[bit_pos/8] & (1 << (bit_pos % 8))) == 0) {
      return false;
    }
  }
  return true;
}

下面进行了一组测试，设置期望的false positive probability为0.1，模拟key从10000增长到100000的场景，观察真实的false positive probability的情况：

key_nums_=10000 expected false positive rate=0.1 real false positive rate=0.1252
key_nums_=20000 expected false positive rate=0.1 real false positive rate=0.1252
key_nums_=30000 expected false positive rate=0.1 real false positive rate=0.1257
key_nums_=40000 expected false positive rate=0.1 real false positive rate=0.1211
key_nums_=50000 expected false positive rate=0.1 real false positive rate=0.1277
key_nums_=60000 expected false positive rate=0.1 real false positive rate=0.1263
key_nums_=70000 expected false positive rate=0.1 real false positive rate=0.126
key_nums_=80000 expected false positive rate=0.1 real false positive rate=0.1219
key_nums_=90000 expected false positive rate=0.1 real false positive rate=0.1265
key_nums_=100000 expected false positive rate=0.1 real false positive rate=0.1327

由于实现的时候，会对k进行取整，根据取整后的结果(k=3)，计算出来的理论值是0.1250，可以，看出实际测出来的值和理论值差别不大。

优化

前面实现的版本中，多次调用了hash_func函数，这对于计算比较长的字符串的hash的开销是比较大的，为了模拟这种场景，插入1000w行的数据，使用perf top来抓取其性能数据，结果如下：

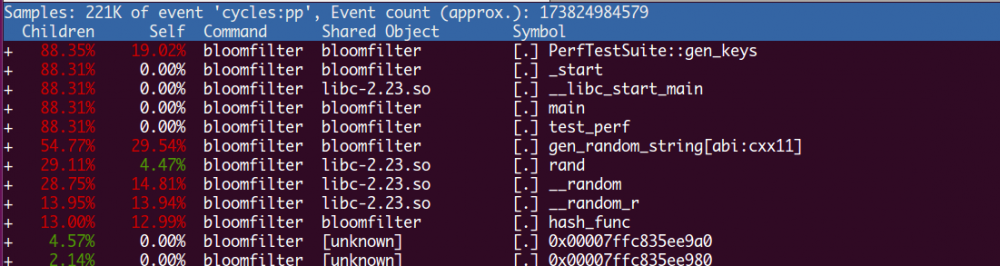
BloomFilter原理，实现及优化

如上图，除了生成数据的函数外，占用CPU最高的就属于hash_func了，占用了13%的CPU。

分析之前的代码可以知道，insert和key_may_match时，都会多次调用hash_func，这个开销是比较大的。

leveldb和维基百科中都有提到，根据之前的研究，可以采用两次hash的方式来替代上述的多次的计算，基本的思路如下：

template<typename T>
void BloomFilter<T>::insert2(const T &key)
{ 
  uint32_t hash_val = key.hash(0xbc9f1d34);
  const uint32_t delta = (hash_val >> 17) | (hash_val << 15);
  for (int i = 0; i < k_; ++i) {
    const uint32_t bit_pos = hash_val % m_;
    bits_[bit_pos/8] |= 1 << (bit_pos % 8);
    hash_val += delta;
  }
}

即先用通常的hash函数计算一次，然后，使用移位操作计算一次，最后，k次计算的时候，不断累加两次的结果。

经过优化后，性能数据图如下：

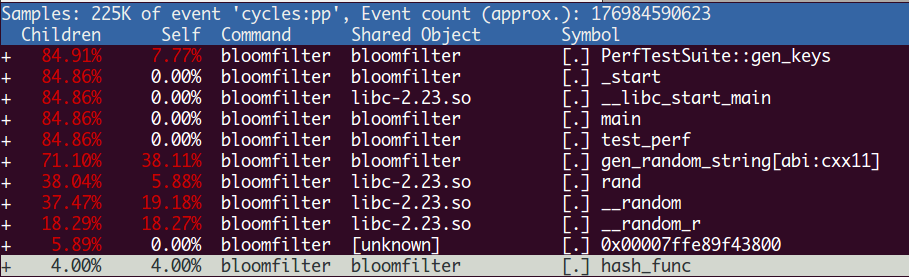
BloomFilter原理，实现及优化

和之前性能图对比发现，hash_func的CPU使用率已经减少到4%了。

对比完性能之后，我们还需要对比hash函数按照如此优化后，false positive probability的变化情况：

before_opt
key_nums_=10000 expected false positive rate=0.1 real false positive rate=0.1252
key_nums_=20000 expected false positive rate=0.1 real false positive rate=0.1252
key_nums_=30000 expected false positive rate=0.1 real false positive rate=0.1257
key_nums_=40000 expected false positive rate=0.1 real false positive rate=0.1211
key_nums_=50000 expected false positive rate=0.1 real false positive rate=0.1277
key_nums_=60000 expected false positive rate=0.1 real false positive rate=0.1263
key_nums_=70000 expected false positive rate=0.1 real false positive rate=0.126
key_nums_=80000 expected false positive rate=0.1 real false positive rate=0.1219
key_nums_=90000 expected false positive rate=0.1 real false positive rate=0.1265
key_nums_=100000 expected false positive rate=0.1 real false positive rate=0.1327
after_opt
key_nums_=10000 expected false positive rate=0.1 real false positive rate=0.1244
key_nums_=20000 expected false positive rate=0.1 real false positive rate=0.1327
key_nums_=30000 expected false positive rate=0.1 real false positive rate=0.134
key_nums_=40000 expected false positive rate=0.1 real false positive rate=0.1389
key_nums_=50000 expected false positive rate=0.1 real false positive rate=0.1342
key_nums_=60000 expected false positive rate=0.1 real false positive rate=0.1548
key_nums_=70000 expected false positive rate=0.1 real false positive rate=0.141
key_nums_=80000 expected false positive rate=0.1 real false positive rate=0.1536
key_nums_=90000 expected false positive rate=0.1 real false positive rate=0.1517
key_nums_=100000 expected false positive rate=0.1 real false positive rate=0.154

优化后，最大的false positive probability增长了2%左右，这个可以增加k来弥补，因为，优化后的hash算法，在k增长时，带来的开销相对来讲不大。

备注，本节采用perf抓取性能数据图，命令如下

sudo perf record -a --call-graph dwarf -p 9125 sleep 60
sudo perf report -g graph

本文的代码在 bloomfilter.cpp ，使用文档在 ReadMe 。

PS:

本博客更新会在第一时间推送到微信公众号，欢迎大家关注。

BloomFilter原理，实现及优化

参考文献

bloomfilter wikipage
Less Hashing, Same Performance:Building a Better Bloom Filter

原文 http://oserror.com/backend/bloomfilter/

正文到此结束

所属分类：编程技术

本文标签： 测试代码总结微信公众号数据参数 ACE UI 组织 Word map list 博客 key 删除 struct CTO http id ip 空间 src 希望 db 时间 build ORM
版权声明： 本文为互联网转载文章，出处已在文章中说明(部分除外)。如果侵权，请联系本站长删除，谢谢。
本文海报： 生成海报一生成海报二

其他链接

关于本站

本站定位：个人技术类博客

本站作用：写博客、记日志、闲聊扯淡鼓捣技术。

问题交流

BloomFilter原理，实现及优化

BloomFilter的使用场景

BloomFilter的原理

原理

参数如何取值

BloomFilter实现及优化

基本版实现

初始化

插入

判断是否存在

优化

参考文献

热门推荐

相关文章

说给你听

本文目录

随机标签

书籍教程

近期评论

网站信息

其他链接

关于本站

问题交流