每日一博 | PageRank 算法计算网页的价值
现假设有A,B,C,D,E五个网页，其中
1) A网页有链接指向B,C,D,E
2) B网页有链接指向A,D
3) C网页有链接指向A,D
4) D网页有链接指向C
5) E网页有链接指向A,C
A 请写出这个网页链接结构的Google矩阵，目测你认为哪个页面的重要性(PR值)最高？
B 手动或编程计算这5个页面的PR值，可以使用任何你熟悉的编程语言;
C 指出当页面较多的时候，计算PR的主要困难在什么地方，Map-Reduce是怎么解决这个难题的?
一、Google矩阵
将上述问题进行数学建模，如下：
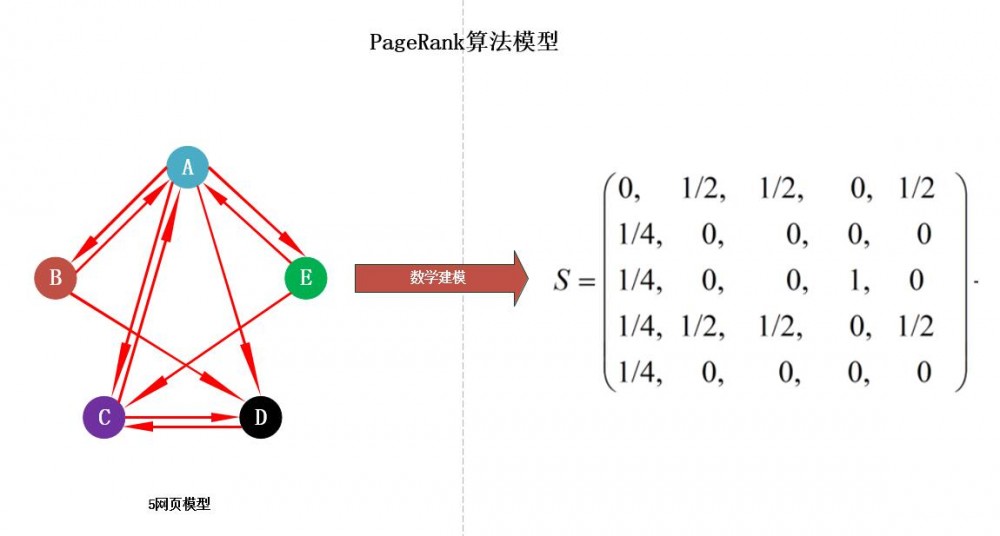
二、网页价值计算（计算PageRank值）
PageRank算法的数学原理如下：
得到初始矩阵后，我们就可以得到PR值，当只有a概率的用户会点击网页链接，剩下(1-a)概率的用户会跳到无关的页面上去，而访问的页面恰好是这5个页面中A的概率只有(1-a)/5（a是阻尼系数，Google取a等于0.85），所以真正的Google矩阵 ：
于是得到q（n)=G*q(n-1),特征向量q的初始值为值为1的5*1矩阵，直到q（n)=q(n-1)，q(n)就是PR的值。
将上述的思想抽象成一个数学函数：
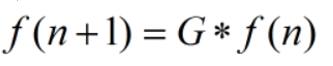
当f(n+1)约等于f(n)，此时的PageRank值即为f(n)。
三、编程实现
public class PageRank {
/**
* 矩阵g乘以矩阵p
* @param g
* @param p
* @return 矩阵g乘以矩阵p的结果矩阵
*/
private static double[] multiMatrix(double[][] g, double[] p){
double[] multiResult = new double[p.length];
for(int i=0; i<g.length; i++){
double rowResult = 0.0f;
for(int j=0; j<g.length; j++){
rowResult+=g[i][j]*p[j];
}
multiResult[i] = rowResult;
}
return multiResult;
}
/**
* 根据初始矩阵计算真正的Google矩阵
* @param 初始矩阵
* @param weight
* @param oneMatrix
* @return 真正的Google矩阵
*/
private static void getGoogleMatrix(double[][] transitionMatrix, double weight){
//transitionMatrix*weight
for(int i=0; i<transitionMatrix.length; i++){
for(int j=0; j<transitionMatrix.length; j++){
transitionMatrix[i][j] *= weight;
transitionMatrix[i][j] += (1-weight)/transitionMatrix.length;
}
}
}
/**
* 如果pageRankN=pageRankN_1,返回true；否则，返回false
* @param pageRankN
* @param pageRankN_1
* @return
*/
private static boolean compareMatrix(double[] pageRankN, double[] pageRankN_1){
for(int i=0; i<pageRankN.length; i++){
if(pageRankN[i]-pageRankN_1[i]>0.0000001){
return false;
}
}
return true;
}
/**
*
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
double[][] transitionMatrix={
{0, 1/2f, 1/2f, 0, 1/2f},
{1/4f, 0, 0, 0, 0},
{1/4f, 0, 0, 1f, 0},
{1/4f, 1/2f, 1/2f, 0, 1/2f},
{1/4f, 0, 0, 0, 0}
};//初始矩阵
double[] p={1,1,1,1,1};
double weight = 0.85f; //a的值
//真正的Google矩阵
getGoogleMatrix(transitionMatrix, weight);
//输出看一下
// for(int i=0; i<transitionMatrix.length; i++){
// for(int j=0; j<transitionMatrix.length; j++){
// System.out.print(transitionMatrix[i][j]);
// System.out.print(" ");
// }
// System.out.println();
// }
//q（n)=G*q(n-1),如果q(n)=q(n-1),q(n)是PageRank
double[] pageRank = multiMatrix(transitionMatrix, p);
while(!compareMatrix(pageRank, p)){
p = pageRank;
pageRank = multiMatrix(transitionMatrix, p);
}
for(int i=0; i<pageRank.length; i++){
System.out.println(pageRank[i]);
}
}
}
计算结果：
1.1724915755493341 0.3991544277616714 1.6075535417744635 1.4216460271528633 0.3991544277616714
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
