转载

构造Y组合子

2016.12.07 17:12:37

构造Y组合子

Y组合子（Y-Combinator）是Lambda演算的一部分，也是FP编程中为人所津津乐道的一种方法。对于FP程序员来讲，估计也仍有不少人对其要么陌生、要么茫茫然。

Y组合子能够神奇地利用匿名函数/Lambda的方式来表述递归调用。Y组合子或不动点组合子的概念可以参考各类百科，这里就不再赘述。

由于最近在钻研Go语言，因此这里就用Go语言进行描述（文章最后也会列出其他几种语言的Y组合子实现）。但Y组合子的概念实现思路都是一致的，掌握了思路，用其他语言实现应该没问题。

话说回来，由于Go语言的类型语言特点，在Go中实现Y组合子很容易被函数定义绕晕了，动态语言则实现起来相对轻松一些。

接下来一步步解释Y组合子构建思路。

示例描述

在这里，我们随意选择了「The Go Programming Language」中的一个例子，作为我们的讲解案例：

func comma(s string) string {
    n := len(s)
    if n <= 3 {
        return s
    }
    return comma(s[:n-3]) + "," + s[n-3:]
}

该示例用来对 1234567890 这样的字符串进行自右往左每隔3个字符加一个逗号： 1,234,567,890 。

这是构建递归调用的传统思路，一般情况下，我们的递归就是像上述代码这样实现的。可以称之为一般性递归（Natural Recursion）。

Y组合子构建

一迈出构建Y组合子的第一步

我们可以发现，在一般性递归中，必须有个函数名，才能使用递归调用。而Y组合子的神奇之处就在于，它能够利用匿名函数/Lambda的方式来表述递归调用。

这是如何做到的？要消除函数名，关键是构建一个能够“自己调用自己”的匿名函数——这是很自然就能想到的，否则无法消除函数名。

下面，看看我们是怎么玩的。

纵使是匿名函数，我们姑且也给这个“无名”一个名字—— f ，因此 f 就变成了（伪代码）：

f{
    return f(s[:n-3]) + ...
}

接下来，我们就需要确实消除这个“无名”的名，这可听起来像是什么高深莫测、难以理解的高深武功呐。别急，一步步来。

首先，我们需要添加一个真正的匿名函数作为包裹函数（伪代码）：

func(f) {
    return ...
}

这里的 return 该返回啥呢？我们知道 f 是个递归，如果只返回 f 是不够的，那跟直接使用 comma 没什么区别，反而造成内层的 f(s[:n-3]) 递归调用无法实现，因为——“无名”。

要返回一个匿名形式的递归函数，也就是要返回一个不断调用自身的函数，其形式为：

f(f)

这个很关键。所以有了这样的代码（伪代码）：

func(f) {
    return f(f)
}

上述伪代码就实现了匿名函数递归调用自身的功能，外层加了个包裹函数是为了返回这个递归调用的匿名函数 f(f) 。

不管怎么变来变去的，我们要的是 comma 的最初实现。包装器的返回类型必然跟 comma 函数的类型定义一样：

func(string) string

所以，我们定义一个 baseFnType ，其跟 comma 的类型定义一样：

type baseFnType func(string) string

由于匿名函数递归调用自身， f 的参数必须接受自身，同时 f 最终也是返回一个 baseFnType 类型，这样才能跟包装器的返回类型一致：

type fnType2 func(fnType2) baseFnType

看看 fnType2 ，参数是自己，返回是 baseFnType 类型—— fnType2 也是一个“递归类型”。

func(f fnType2) baseFnType {
    return f(f)
}

最后，如何调用这个匿名递归函数呢？

很容易，把逻辑以匿名函数的方式包装一下传递给这个匿名递归调用即可：

comma :=
    func(f fnType2) baseFnType {
        return f(f)
    }(func(f fnType2) baseFnType {
        return func(s string) string {
            n := len(s)
            if n <= 3 {
                return s
            }
            return f(f)(s[:n-3]) + "," + s[n-3:]
        }
    })

等等，为何最后有个 return f(f)... ？怎么会是 f(f) 呢？因为前面说了，递归调用的匿名函数现在是 f(f) 。

好了，先来试试看：

fmt.Printf("%v/n", comma("1234567890"))

很神奇，真的输出了：

1,234,567,890

最关键的一步迈出去了。

二简单才好

简化，遵循Scheme十诫之第八戒——“使用辅助函数来抽象表示方式”

看看逻辑混搭在这个函数里也是怪难受的，我们首先来分离逻辑和骨架。

首先把函数调用同逻辑处理做一定的分离：

comma :=
    func(f fnType2) baseFnType {
        return f(f)
    }(func(f fnType2) baseFnType {
        g := func(s string) string {
            return f(f)(s)
        }

        return func(s string) string {
            n := len(s)
            if n <= 3 {
                return s
            }
            return g(s[:n-3]) + "," + s[n-3:]
        }
    })

然后我们需要为：

return func(s string) string {
    ...
}

里面的业务逻辑定义一个函数，然后通过这个函数，把业务逻辑“注入”进来，这样，以后不同的业务逻辑都能够通过这个函数“注入”进来，内部的骨架就不用调整了。因此，该函数也是个包装器函数。

在此之前我们需要定义一个包装器的函数类型，该类型以 baseFnType 为参数类型——因为我们传入的函数类型是 func(s string) string ，根据 return f(f)(s[:n-3]) + "," + s[n-3:] ，包装器返回的也是一个 baseFnType 类型。因此，我们就有了：

type fnType1 func(baseFnType) baseFnType

以下是简化后的代码：

comma :=
    func(fn fnType1) baseFnType {
        return func(f fnType2) baseFnType {
            return f(f)
        }(func(f fnType2) baseFnType {
            g := func(s string) string {
                return f(f)(s)
            }

            return fn(g)
        })
    }

来试试代码正确与否：

comma :=
    func(fn fnType1) baseFnType {
        return func(f fnType2) baseFnType {
            return f(f)
        }(func(f fnType2) baseFnType {
            g := func(s string) string {
                return f(f)(s)
            }

            return fn(g)
        })
    }(func(g baseFnType) baseFnType {
        return func(s string) string {
            n := len(s)
            if n <= 3 {
                return s
            }
            return g(s[:n-3]) + "," + s[n-3:]
        }
    })

fmt.Printf("%v/n", comma("1234567890"))

OK！输出：

1,234,567,890

接下来，我们把 g 定义直接放进到 fn 里：

y :=
    func(fn fnType1) baseFnType {
        return func(f fnType2) baseFnType {
            return f(f)
        }(func(f fnType2) baseFnType {
            return fn(func(s string) string {
                return f(f)(s)
            })
        })
    }

嗯！这就是大名鼎鼎的Y组合子。

来测试一下：

comma :=
    y(func(g baseFnType) baseFnType {
        return func(s string) string {
            n := len(s)
            if n <= 3 {
                return s
            }
            return g(s[:n-3]) + "," + s[n-3:]
        }
    })

fmt.Printf("%v/n", comma("1234567890"))

结果OK！

甚至还可以带入不同逻辑，比如：

upper :=
    y(func(g baseFnType) baseFnType {
        return func(s string) string {
            n := len(s)
            if n == 0 {
                return s
            }
            return g(s[:n-1]) + strings.ToUpper(s[n-1:])
        }
    })

fmt.Printf("%v/n", upper("abcdefghijklmnopqrstuvwxyz."))

将输出：

ABCDEFGHIJKLMNOPQRSTUVWXYZ.

至此本文告一段落。

其他

由于动态语言没有强类型要求，因此实现的Y组合子更简单。下面分别列出Python、JavaScript、Scheme的Y组合子形式。

Python实现：

Y = lambda fn: (lambda f: f(f))(lambda f: fn(lambda s: f(f)(s)))

Y(lambda g:
    lambda s:
        s if len(s)==0
          else g(s[:len(s)-1]) + s[len(s)-1].upper())("abcdefghijklmnopqrstuvwxyz.")

输出：

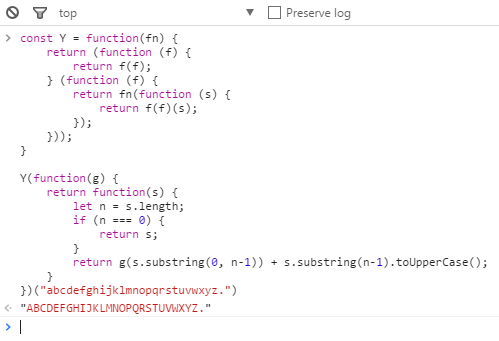
构造Y组合子

JavaScript：

const Y = function(fn) {
    return (function (f) {
        return f(f);
    } (function (f) {
        return fn(function (s) {
            return f(f)(s);
        });
    }));
}

Y(function(g) {
    return function(s) {
        let n = s.length;
        if (n === 0) {
            return s;
        }
        return g(s.substring(0, n-1)) + s.substring(n-1).toUpperCase();
    }
})("abcdefghijklmnopqrstuvwxyz.")

输出：

构造Y组合子

Scheme：

(define Y
(lambda (fn)
    ((lambda (f)
    (f f)) (lambda (f)
            (fn (lambda (s) ((f f) s)))))))

((Y (lambda (g)
(lambda (s)
    (cond
    ((null? s) '())
    (else
        (cons (string-upcase (car s)) (g (cdr s)))))))) '("a" "b" "c" "d" "e"))

输出：

构造Y组合子