转载

机器学习算法比较

作者：刘帝伟

原文：机器学习算法比较

本文主要回顾下几个常用算法的适应场景及其优缺点！（提示：部分内容摘自网络）。

机器学习算法太多了，分类、回归、聚类、推荐、图像识别领域等等，要想找到一个合适算法真的不容易，所以在实际应用中，我们一般都是采用启发式学习方式来实验。通常最开始我们都会选择大家普遍认同的算法，诸如SVM，GBDT，Adaboost，现在深度学习很火热，神经网络也是一个不错的选择。假如你在乎精度（accuracy）的话，最好的方法就是通过交叉验证（cross-validation）对各个算法一个个地进行测试，进行比较，然后调整参数确保每个算法达到最优解，最后选择最好的一个。但是如果你只是在寻找一个“足够好”的算法来解决你的问题，或者这里有些技巧可以参考，下面来分析下各个算法的优缺点，基于算法的优缺点，更易于我们去选择它。

偏差&方差

在统计学中，一个模型好坏，是根据偏差和方差来衡量的，所以我们先来普及一下偏差(bias)和方差(variance)：

偏差：描述的是预测值（估计值）的期望E’与真实值Y之间的差距。偏差越大，越偏离真实数据。

Bias [/hat{f}(x)] = E [/hat{f}(x)] – f(x) /

/tag{1} /label{1}

方差：描述的是预测值P的变化范围，离散程度，是预测值的方差，也就是离其期望值E的距离。方差越大，数据的分布越分散。

Var [/hat{f}(x)] = E [(/hat{f}(x) – E[/hat{f}(x)])^2]

/tag{2} /label{2}

模型的真实误差是两者之和，如公式/eqref{3}：

E /left [(y – /hat{f}(x))^2 /right ] = Bias [/hat{f}(x)]^2 Var[/hat{f}(x)] /sigma^2

/tag{3} /label{3}

通常情况下，如果是小训练集，高偏差/低方差的分类器（例如，朴素贝叶斯NB）要比低偏差/高方差大分类的优势大（例如，KNN），因为后者会发生过拟合（overfiting）。然而，随着你训练集的增长，模型对于原数据的预测能力就越好，偏差就会降低，此时低偏差/高方差的分类器就会渐渐的表现其优势（因为它们有较低的渐近误差），而高偏差分类器这时已经不足以提供准确的模型了。

当然，你也可以认为这是生成模型（如NB）与判别模型（如KNN）的一个区别。

为什么说朴素贝叶斯是高偏差低方差?

以下内容引自知乎：

首先，假设你知道训练集和测试集的关系。简单来讲是我们要在训练集上学习一个模型，然后拿到测试集去用，效果好不好要根据测试集的错误率来衡量。但很多时候，我们只能假设测试集和训练集的是符合同一个数据分布的，但却拿不到真正的测试数据。这时候怎么在只看到训练错误率的情况下，去衡量测试错误率呢？

由于训练样本很少（至少不足够多），所以通过训练集得到的模型，总不是真正正确的。（就算在训练集上正确率100%，也不能说明它刻画了真实的数据分布，要知道刻画真实的数据分布才是我们的目的，而不是只刻画训练集的有限的数据点）。而且，实际中，训练样本往往还有一定的噪音误差，所以如果太追求在训练集上的完美而采用一个很复杂的模型，会使得模型把训练集里面的误差都当成了真实的数据分布特征，从而得到错误的数据分布估计。这样的话，到了真正的测试集上就错的一塌糊涂了（这种现象叫过拟合）。但是也不能用太简单的模型，否则在数据分布比较复杂的时候，模型就不足以刻画数据分布了（体现为连在训练集上的错误率都很高，这种现象较欠拟合）。过拟合表明采用的模型比真实的数据分布更复杂，而欠拟合表示采用的模型比真实的数据分布要简单。

在统计学习框架下，大家刻画模型复杂度的时候，有这么个观点，认为Error = Bias Variance。这里的Error大概可以理解为模型的预测错误率，是有两部分组成的，一部分是由于模型太简单而带来的估计不准确的部分（Bias），另一部分是由于模型太复杂而带来的更大的变化空间和不确定性（Variance）。

所以，这样就容易分析朴素贝叶斯了。它简单的假设了各个数据之间是无关的，是一个被 严重简化了的模型 。所以，对于这样一个简单模型，大部分场合都会Bias部分大于Variance部分，也就是说高偏差而低方差。

在实际中，为了让Error尽量小，我们在选择模型的时候需要平衡Bias和Variance所占的比例，也就是平衡over-fitting和under-fitting。

偏差、方差、模型复杂度三者之间的关系使用下图表示会更容易理解：

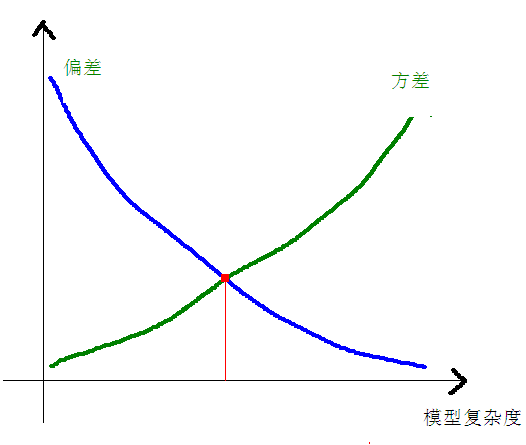
机器学习算法比较

当模型复杂度上升的时候，偏差会逐渐变小，而方差会逐渐变大。

常见算法优缺点

1. 朴素贝叶斯

朴素贝叶斯属于生成式模型（关于生成模型和判别式模型，主要还是在于是否需要求联合分布），比较简单，你只需做一堆计数即可。如果注有条件独立性假设（一个比较严格的条件），朴素贝叶斯分类器的收敛速度将快于判别模型，比如逻辑回归，所以你只需要较少的训练数据即可。即使NB条件独立假设不成立，NB分类器在实践中仍然表现的很出色。它的主要缺点是它不能学习特征间的相互作用，用mRMR中R来讲，就是特征冗余。引用一个比较经典的例子，比如，虽然你喜欢Brad Pitt和Tom Cruise的电影，但是它不能学习出你不喜欢他们在一起演的电影。

优点：

朴素贝叶斯模型发源于古典数学理论，有着坚实的数学基础，以及稳定的分类效率。
对小规模的数据表现很好，能个处理多分类任务，适合增量式训练；
对缺失数据不太敏感，算法也比较简单，常用于文本分类。

缺点：

需要计算先验概率；
分类决策存在错误率；
对输入数据的表达形式很敏感。

2. Logistic Regression（逻辑回归）

逻辑回归属于判别式模型，同时伴有很多模型正则化的方法（L0， L1，L2，etc），而且你不必像在用朴素贝叶斯那样担心你的特征是否相关。与决策树、SVM相比，你还会得到一个不错的概率解释，你甚至可以轻松地利用新数据来更新模型（使用在线梯度下降算法-online gradient descent）。如果你需要一个概率架构（比如，简单地调节分类阈值，指明不确定性，或者是要获得置信区间），或者你希望以后将更多的训练数据快速整合到模型中去，那么使用它吧。

Sigmoid函数：表达式为公式/eqref{4}.

f(x) = /frac{1}{1 e^{-x}}

/tag{4}/label{4}

优点：

实现简单，广泛的应用于工业问题上；
分类时计算量非常小，速度很快，存储资源低；
便利的观测样本概率分数；
对逻辑回归而言，多重共线性并不是问题，它可以结合L2正则化来解决该问题；

缺点：

当特征空间很大时，逻辑回归的性能不是很好；
容易 欠拟合 ，一般准确度不太高
不能很好地处理大量多类特征或变量；
只能处理两分类问题（在此基础上衍生出来的softmax可以用于多分类），且必须 线性可分 ；
对于非线性特征，需要进行转换；

3.线性回归

线性回归是用于回归的，它不像Logistic回归那样用于分类，其基本思想是用 梯度下降法 对最小二乘法形式的误差函数进行优化，当然也可以用normal equation直接求得参数的解，结果为：

/hat{w}=(X^{T}X)^{-1}X^Ty

/tag{5}/label{5}

而在LWLR（局部加权线性回归）中，参数的计算表达式为:

/hat{w}=(X^{T}WX)^{-1}X^TWy

/tag{6}/label{6}

由此可见LWLR与LR不同，LWLR是一个非参数模型，因为每次进行回归计算都要遍历训练样本至少一次。

优点：实现简单，计算简单；

缺点：不能拟合非线性数据.

4.最近邻算法——KNN

KNN即最近邻算法，其主要过程为：

1. 计算训练样本和测试样本中每个样本点的距离（常见的距离度量有欧式距离，马氏距离等）；
2. 对上面所有的距离值进行排序(升序)；
3. 选前k个最小距离的样本；
4. 根据这k个样本的标签进行投票，得到最后的分类类别；

如何选择一个最佳的K值，这取决于数据。一般情况下，在分类时较大的K值能够减小噪声的影响，但会使类别之间的界限变得模糊。一个较好的K值可通过各种启发式技术来获取，比如，交叉验证。另外噪声和非相关性特征向量的存在会使K近邻算法的准确性减小。近邻算法具有较强的一致性结果，随着数据趋于无限，算法保证错误率不会超过贝叶斯算法错误率的两倍。对于一些好的K值，K近邻保证错误率不会超过贝叶斯理论误差率。

KNN算法的优点

理论成熟，思想简单，既可以用来做分类也可以用来做回归；
可用于非线性分类；
训练时间复杂度为O(n)；
对数据没有假设，准确度高，对outlier不敏感；

缺点

计算量大（体现在距离计算上）；
样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少）效果差；
需要大量内存；

5.决策树

决策树的一大优势就是易于解释。它可以毫无压力地处理特征间的交互关系并且是非参数化的，因此你不必担心异常值或者数据是否线性可分（举个例子，决策树能轻松处理好类别A在某个特征维度x的末端，类别B在中间，然后类别A又出现在特征维度x前端的情况）。它的缺点之一就是不支持在线学习，于是在新样本到来后，决策树需要全部重建。另一个缺点就是容易出现过拟合，但这也就是诸如随机森林RF（或提升树boosted tree）之类的集成方法的切入点。另外，随机森林经常是很多分类问题的赢家（通常比支持向量机好上那么一丁点），它训练快速并且可调，同时你无须担心要像支持向量机那样调一大堆参数，所以在以前都一直很受欢迎。

决策树中很重要的一点就是选择一个属性进行分枝，因此要注意一下信息增益的计算公式，并深入理解它。

信息熵的计算公式如下:

H=-/sum^{n}_{i=1}p(x_i)log_2p(x_i)

/tag{7}/label{7}

其中的n代表有n个分类类别（比如假设是二类问题，那么n=2）。分别计算这2类样本在总样本中出现的概率p1和p2，这样就可以计算出未选中属性分枝前的信息熵。

现在选中一个属性$x_i$用来进行分枝，此时分枝规则是：如果$x_i=v$的话，将样本分到树的一个分支；如果不相等则进入另一个分支。很显然，分支中的样本很有可能包括2个类别，分别计算这2个分支的熵H1和H2,计算出分枝后的总信息熵H’ =p1 H1 p2 H2,则此时的信息增益ΔH = H – H’。以信息增益为原则，把所有的属性都测试一边，选择一个使增益最大的属性作为本次分枝属性。

决策树自身的优点

计算简单，易于理解，可解释性强；
比较适合处理有缺失属性的样本；
能够处理不相关的特征；
在相对短的时间内能够对大型数据源做出可行且效果良好的结果。

缺点

容易发生过拟合（随机森林可以很大程度上减少过拟合）；
忽略了数据之间的相关性；
对于那些各类别样本数量不一致的数据，在决策树当中,信息增益的结果偏向于那些具有更多数值的特征（只要是使用了信息增益，都有这个缺点，如RF）。

5.1 Adaboosting

Adaboost是一种加和模型，每个模型都是基于上一次模型的错误率来建立的，过分关注分错的样本，而对正确分类的样本减少关注度，逐次迭代之后，可以得到一个相对较好的模型。该算法是一种典型的boosting算法，其加和理论的优势可以使用Hoeffding不等式得以解释。有兴趣的同学可以阅读下笔者后面写的这篇文章 Adaboost – 新的角度理解权值更新策略 .下面总结下它的优缺点。

优点

Adaboost是一种有很高精度的分类器。
可以使用各种方法构建子分类器，Adaboost算法提供的是框架。
当使用简单分类器时，计算出的结果是可以理解的，并且弱分类器的构造极其简单。
简单，不用做特征筛选。
不易发生overfitting。

关于随机森林和GBDT等组合算法，参考这篇文章：机器学习-组合算法总结

缺点：对outlier比较敏感

6.SVM支持向量机

支持向量机，一个经久不衰的算法，高准确率，为避免过拟合提供了很好的理论保证，而且就算数据在原特征空间线性不可分，只要给个合适的核函数，它就能运行得很好。在动辄超高维的文本分类问题中特别受欢迎。可惜内存消耗大，难以解释，运行和调参也有些烦人，而随机森林却刚好避开了这些缺点，比较实用。

优点

可以解决高维问题，即大型特征空间；
能够处理非线性特征的相互作用；
无需依赖整个数据；
可以提高泛化能力；

缺点

当观测样本很多时，效率并不是很高；
对非线性问题没有通用解决方案，有时候很难找到一个合适的核函数；
对缺失数据敏感；

对于核的选择也是有技巧的（libsvm中自带了四种核函数：线性核、多项式核、RBF以及sigmoid核）：

第一，如果样本数量小于特征数，那么就没必要选择非线性核，简单的使用线性核就可以了；
第二，如果样本数量大于特征数目，这时可以使用非线性核，将样本映射到更高维度，一般可以得到更好的结果；
第三，如果样本数目和特征数目相等，该情况可以使用非线性核，原理和第二种一样。

对于第一种情况，也可以先对数据进行降维，然后使用非线性核，这也是一种方法。

7. 人工神经网络的优缺点

人工神经网络的优点：

分类的准确度高；
并行分布处理能力强,分布存储及学习能力强，
对噪声神经有较强的鲁棒性和容错能力，能充分逼近复杂的非线性关系；
具备联想记忆的功能。

人工神经网络的缺点：

神经网络需要大量的参数，如网络拓扑结构、权值和阈值的初始值；
不能观察之间的学习过程，输出结果难以解释，会影响到结果的可信度和可接受程度；
学习时间过长,甚至可能达不到学习的目的。

8、K-Means聚类

之前笔者写过一篇关于K-Means聚类的文章，参见机器学习算法-K-means聚类。关于K-Means的推导，里面可是有大学问的，蕴含着强大的EM思想。

优点

算法简单，容易实现；
对处理大数据集，该算法是相对可伸缩的和高效率的，因为它的复杂度大约是O(nkt)，其中n是所有对象的数目，k是簇的数目,t是迭代的次数。通常k<<n。这个算法通常局部收敛。
算法尝试找出使平方误差函数值最小的k个划分。当簇是密集的、球状或团状的，且簇与簇之间区别明显时，聚类效果较好。