转载

朋友你听说过尾递归吗

1. 尾递归

说起 尾递归 就不能不提一下 尾调用(Tail Call) 。

尾调用：在函数的最后一步调用另外一个函数。

function func(){
    // ... other code
    return otherFunc();// 尾调用
}

尾递归：在函数的最后一步调用自身

function func(){
    // ... other code
    return func();// 尾递归
}

2. 尾调用和非尾调用

说到递归，那就必然要以斐波那契数列为例子

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……

简单的说，斐波那契数列中的每一项都是前两项的和。

即 F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>2，n∈N*）

2.1 常见版本

// 实现出来长这样
function fibo(n) {
    if (n <= 0) {
        return 0;
    } else if (n === 1) {
        return 1;
    }
    return fibo(n - 1) + fibo(n - 2)
}

所以手动模拟一下计算fibo(5)的调用栈，大概是这样的

fibo(5)
fibo(4) + fibo(3)
fibo(3) + fibo(2)+  fibo(3)
fibo(2) + fibo(1) + fibo(2)+  fibo(3)
2 + fibo(2) +  fibo(3)
3 + fibo(3)
3 + fibo(2) + fibo(1)
3 + 2
5

在计算的过程中，堆栈需要不停的记录每一层次调用的详细信息（如参数、局部变量、返回地址等等），以确保该层次的操作完成，能返回到上一层次，这些信息再少也会占用一定空间，成千上万个此类空间累积起来，自然就超过线程的栈空间了。于是 stackOverflow 异常就被抛出了。

2.2 尾递归版本

function fibo(n, num1 = 1, num2 = 1) {
    if (n <= 0) {
        return 0;
    } else if (n === 1) {
        return num1;
    }
    return fibo4(n - 1, num2, num1 + num2);
}

同样手动模拟一下调用栈

fibo(5)
fibo(4, 1, 2)
fibo(3, 2, 3)
fibo(2, 3, 5)
fibo(1, 5, 8)

你会发现，尾调用作为函数的最后一步操作，它在某些场景下不需要保存外层函数的调用记录，因为这些信息不会再被用到了（这里是作为参数传入下一次调用了），所以可以以上层调用帧作为尾调用的调用环境。即

fibo(5);
// 等同于调用
fibo(1, 5, 8);// 中间的调用帧都不需要保存

使用尾递归，取消过多的堆栈记录，而只记录最外层和当前层的信息，完成计算后，立刻返回到最上层。这也就不会有栈溢出的问题，同时减少了内存以及上下文切换的损耗。

细心的朋友也发现了，尾递归的本质实际上就是将方法需要的上下文通过方法的参数传递进下一次调用之中，以达到去除上层依赖。

但是这同样会引入一些让使用者费解的调用参数，上文使用ES6的默认参数解决调用暴露函数列表的问题，但是依旧可能因为用户多传入的参数导致计算结果不正确。所以你可能需要一些其他的手段解决API的问题，例如封装一层调用方法，函数柯理化等。

3. 性能对比

// 常规递归写法
function fibo(n) {
    if (n <= 0) {
        return 0;
    } else if (n === 1) {
        return 1;
    }
    return fibo(n - 1) + fibo(n - 2)
}

// 常规循环写法
function fibo2(n) {
    if (n <= 0) {
        return 0;
    } else if (n === 1) {
        return 1;
    }
    let x = 0,
        y = 1,
        sum = 0;
    for (let i = 2; i <= n; i++) {
        sum = x + y;
        x = y;
        y = sum;
    }
    return sum;
}

// 公式法
function fibo3(n) {
    if (n <= 0)
        return 0;
    else {
        const sqrtFive = Math.sqrt(5);
        const res = (Math.pow(0.5 + sqrtFive / 2, n) - Math.pow(0.5 - sqrtFive / 2, n)) / sqrtFive;
        return Math.round(res);
    }
}

// 尾递归写法
function fibo4(n, num1 = 1, num2 = 1) {
    if (n <= 0) {
        return 0;
    } else if (n === 1) {
        return num1;
    }
    return fibo4(n - 1, num2, num1 + num2);
}

function test() {
    let tick = Date.now();
    console.log(fibo(50), Date.now() - tick);
    tick = Date.now();
    console.log(fibo2(500), Date.now() - tick);
    tick = Date.now();
    console.log(fibo3(500), Date.now() - tick);
    tick = Date.now();
    console.log(fibo4(500), Date.now() - tick);
    tick = Date.now();
}

运行结果：

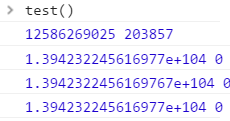
通过运行结果我们可以得到一些结论：

慎用直接递归的方式，不仅会带来极差的运行效率，同时会导致浏览器直接无响应。在浏览器环境中，一些代价高昂的计算会导致糟糕的用户体验，因为一个页面的用户界面无响应多数是由于在运行js代码。
尾递归有着与循环同样优秀的计算性能 ，使用尾递归可以同时拥有着循环的性能以及递归的 数学表达能力 。

4. 一个栈溢出的例子

// 计算1-N的累加值
function f(n) {
    if (n <= 1) {
        return 1;
    }
    return f(n - 1) + n;
}
f(100000);

调用结果：

// 计算1-N的累加值（尾递归）
function f(n, sum = 1) {
    if (n <= 1) {
        return sum;
    }
    return f(n - 1, sum + n);
}
f(100000);

调用结果：

什么鬼，说好的尾递归优化呢？

5. PTC与STC

ES6标准规定了尾调用不会创建额外的调用帧。

在严格模式下尾调用不会造成调用栈溢出。

Proper Tail Calls(PTC)已经实现了，但是还未部署，该功能仍然在 TC39 标准委员会中讨论。

5.1 PTC存在的问题

1 性能

大部分实现者和开发者认为PTC是一种优化策略，使得代码跑的更快。但是可能由于其他的约束，例如兼容以前的功能或顺应标准，部分团队在实现的时候牺牲了性能。

2 开发者工具

在PTC的实现中，许多调用帧都被抛弃了，导致很难再调用栈中调试他们的代码。

// 举个例子
function foo(n) {
  return bar(n*2);// 尾调用
}

function bar() {
  throw new Error();
}

foo(1);
// 由于尾调用优化
// 在Error.stack或者开发者工具中，foo的调用帧被丢掉了。

3 Error.stack

启用PTC导致Javascript异常有了不一致的error.stack信息。

/*
output without PTC
Error
    at bar
    at foo
    at Global Code

output with PTC (note how it appears that bar is called from Global Code)
Error
    at bar
    at Global Code
*/

4 开发者意图

开发者是否真的从PTC中受益了呢，或许开发者根本就不想自动对尾调用进行优化呢？接下来讲到的STC即可避免其他事情重构的危险，有着更明确的语义。

5.2 STC

语义上的尾调用（Syntactic Tail Call）是针对上述PTC的问题而提出的建议。

STC采用类似于 return continue 的语法来明确标识出要进行尾调用优化，而在非尾调用的场景下使用该语法会抛出语法错误异常。

该语法有三种实现形式：

语法级

function factorial(n, acc = 1) {
  if (n === 1) {
    return acc;
  }

  return continue factorial(n - 1, acc * n)
}

函数级

#function() { /* all calls in tail position are tail calls */ }

表达式/调用点

function () { 
    !return expr 
}

更多内容可参考： proposal-ptc-syntax

6. 那么问题来了

挖掘机技术 ... 呸。

我们以斐波那契数列为例子讲解了尾递归的运用方式，并对比了普通递归与尾递归的性能。

通过实验我们能够确定尾递归调用确实帮助我们调优了程序性能(第三节内容)，但是通过第四节的实验我们发现依旧不能避免调用栈溢出的问题，而ES6的标准里面规定了尾调用的优化中是不会创建新的调用帧的。

那么尾递归的方式依旧出现了调用栈溢出的原因究竟是什么呢？

原文 http://imweb.io/topic/584d33049be501ba17b10aaf

正文到此结束

所属分类：编程技术

本文标签： web API src java 调试开发开发者参数 UI 兔子线程 App id CTO IO js 空间 JavaScript ip 代码 http
版权声明： 本文为互联网转载文章，出处已在文章中说明(部分除外)。如果侵权，请联系本站长删除，谢谢。
本文海报： 生成海报一生成海报二

其他链接

关于本站

本站定位：个人技术类博客

本站作用：写博客、记日志、闲聊扯淡鼓捣技术。

问题交流

朋友你听说过尾递归吗

1. 尾递归

2. 尾调用和非尾调用

2.1 常见版本

2.2 尾递归版本

3. 性能对比

4. 一个栈溢出的例子

5. PTC与STC

5.1 PTC存在的问题

5.2 STC

6. 那么问题来了

热门推荐

相关文章

说给你听

本文目录

随机标签

书籍教程

近期评论

网站信息

其他链接

关于本站

问题交流