MYSQL实现ORDER BY LIMIT的方法以及优先队列(堆排序)
一、MYSQL中的LIMIT和ORACLE中的分页
在MYSQL官方文档中描述limit是在结果集中返回你需要的数据,它可以尽快的返回需要的行而不用管剩下的行,
在ORACLE中也有相关的语法比如 12C以前的rownun<n,也是达到同样的效果,同时limit也能做到分页查询如
limit n,m 则代表返回n开始的m行,ORACLE 12C以前也有分页方式但是相对比较麻烦
那么如果涉及到排序呢?我们需要返回按照字段排序后的某几行:
MYSQL:
select * from test order by id limit 51,100
ORACLE 12C以前:
SELECT *
FROM (SELECT tt.*, ROWNUM AS rowno
FROM (SELECT t.*
FROM test t)
ORDER BY id desc) tt
WHERE ROWNUM <= 100) table_alias
WHERE table_alias.rowno > 50;
当然如上的语法如果id列有索引那么就简单了,索引本生就是排序好的,使用索引结构即可,但是如果id列没有索引呢?
那该如何完成,难道把id列全部排序好在返回需要的行?显然这样代价过高,违背了limit中尽快返回需要的行的精神
这样我们必须使用一种合适的算法来完成,那这里就引入的堆排序和优先队列(Priority Queue 简称PQ)。
在MYSQL中执行计划没有完全的表现,执行计划依然为filesort:
mysql> explain select * from testshared3 order by id limit 10,20;
+----+-------------+-------------+------------+------+---------------+------+---------+------+---------+----------+----------------+
| id | select_type | table | partitions | type | possible_keys | key | key_len | ref | rows | filtered | Extra |
+----+-------------+-------------+------------+------+---------------+------+---------+------+---------+----------+----------------+
| 1 | SIMPLE | testshared3 | NULL | ALL | NULL | NULL | NULL | NULL | 1023820 | 100.00 | Using filesort |
+----+-------------+-------------+------------+------+---------------+------+---------+------+---------+----------+----------------+
1 row in set, 1 warning (0.02 sec)
但是根据源码的提示
DBUG_PRINT("info", ("filesort PQ is applicable"));
DBUG_PRINT("info", ("filesort PQ is not applicable"));
注意这里PQ可能弃用,什么时候弃用看后面
可以看到是否启用了PQ也就是优先队列的简写
可以再trace中找到相关说明:
[root@testmy tmp]# cat pq.trace |grep "filesort PQ is applicable"
T@2: | | | | | | | | | | info: filesort PQ is applicable
在ORACLE中使用执行计划:
--------------------------------------------------------------------------------
Plan hash value: 1473139430
--------------------------------------------------------------------------------
| Id | Operation | Name | Rows | Bytes |TempSpc| Cost (%CPU)|
--------------------------------------------------------------------------------
| 0 | SELECT STATEMENT | | 100 | 77900 | | 85431 (1)|
|* 1 | VIEW | | 100 | 77900 | | 85431 (1)|
|* 2 | COUNT STOPKEY | | | | | |
| 3 | VIEW | | 718K| 524M| | 85431 (1)|
|* 4 | SORT ORDER BY STOPKEY| | 718K| 325M| 431M| 85431 (1)|
| 5 | TABLE ACCESS FULL | TEST10 | 718K| 325M| | 13078 (1)|
这里SORT ORDER BY STOPKEY就代表了排序停止,但是ORACLE没有源码没法确切的证据使用了
优先队列和堆排序,只能猜测他使用了优先队列和堆排序
二、堆排序和优先队列
--大顶堆特性(小顶堆相似见代码)
1、必须满足完全二叉树
关于完全二叉树参考
http://blog.itpub.net/7728585/viewspace-2125889/
2、很方便的根据父节点的位置计算出两个叶子结点的位置
如果父节点的位置为i/2
左子节点为 i,右子节点为i+1
这是完全二叉树的特性决定
3、所有子节点都可以看做一个子堆那么所有结点都有
父节点>=左子节点 && 父节点>=右节点
4、很明显的可以找到最大的元素,就是整个堆的根结点
--堆需要完成操作
堆排序方法也是最优队列的实现方法,MYSQL源码中明显的使用了优先队列来优化order by limit n ,估计max也是用的这种算法
当然前提是没有使用到索引的情况下。
根据这些特性明显又是一个递归的成堆的操作。
参考算法导论第六章,里面的插图能够加深理解,这里截取一张构建好的大顶堆
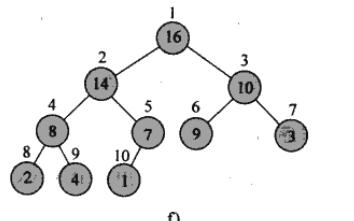
构建方法:自下而上的构建自左向右构建堆,其实就是不断调用维护方法的过程
维护方法:使用递归的逐级下降的方法进行维护,是整个算法的核心内容,搞清楚了维护方法其他任何操作都来自于它。
排序方法:最大元素放到最后,然后逐层下降的方法进行调整。
数据库中的应用:
order by asc/desc limit n:简化的排序而已,只是排序前面n就可以了,不用全部排序完成,性能优越,数据库分页查询大量使用这个算法。参考代码
max/min :a[1]就是最大值,只能保证a[1]>=a[2]&&a[1]>=a[3] 不能保证a[3]>=a[4],堆建立完成后就可以找到MAX值,但是MYSQL max并没有使用这个算法
我在代码中完成了这些操作,代码中有比较详细的注释,这里就不详细说明了。
我使用了2个数组用于作为测试数据
int i,a[11]={0,999,3,2,9,34,5,102,90,2222,1}; //测试数据 a[0]不使用
int b[11]={0,999,3,2,9,999,888888,102,90,2222,111};//测试数据 b[0]不使用
分别求a素组的最大值和最小前3位数字,求b数组的MAX/MIN值,结果如下:
gaopeng@bogon:~/datas$ ./a.out
大顶堆:
order by desc a array limit 3 result:2222 999 102
max values b array reulst:888888
小顶堆:
order by asc a array limit 3 result:1 2 3
min values b array reulst:2
可以看到没问题。
--优先队列:优先队列不同于普通队列先进先出的规则,而定义为以某种规定先出,比如最大先出或者最小先出,这个没什么难度了,不就和数据库的order
by limit是一回事吗?当然是用大顶堆或者小顶堆完成
三、MYSQL中优先队列的接口
MYSQL中的优先队列类在
priority_queue.h中的class Priority_queue : public Less
他实现了很多功能,不过其他功能都很简单主要是堆的维护
下面是MYSQL源码中的堆的维护代码
void heapify(size_type i, size_type last)
{
DBUG_ASSERT(i < size());
size_type largest = i;
do
{
i = largest;
size_type l = left(i);
size_type r = right(i);
if (l < last && Base::operator()(m_container[i], m_container[l]))
{
largest = l;
}
if (r < last && Base::operator()(m_container[largest], m_container[r]))
{
largest = r;
}
if (largest != i)
{
std::swap(m_container[i], m_container[largest]);
}
} while (largest != i);
}
可以看见实际和我写的差不多。
四、MYSQL如何判断是否启用PQ
一般来说快速排序的效率高于堆排序,但是堆排序有着天生的特点可以实现优先队列,来实现
order by limit
(关于快速排序参考:http://blog.itpub.net/7728585/viewspace-2130743/)
那么这里就涉及一个问题,那就是快速排序和最优的队列的临界切换,比如
表A 100W行记录 id列没有索引
select * from a order by id limit 10;
和
select * from a order by id limit 900000,10;
肯定前者应该使用最优队列,而后者实际上要排序好至少900010行数据才能返回。
那么这个时候应该使用快速排序,那么trace信息应该为
filesort PQ is not applicable
[root@testmy tmp]# cat pqdis.trace |grep "filesort PQ "
T@2: | | | | | | | | | | info: filesort PQ is not applicable
那么MYSQL值确定是否使用PQ,其判定接口为check_if_pq_applicable函数,
简单的说MYSQL认为堆排序比快速排序慢3倍如下:
/*
How much Priority Queue sort is slower than qsort.
Measurements (see unit test) indicate that PQ is roughly 3 times slower.
*/
const double PQ_slowness= 3.0;
所以就要进行算法的切换,但是具体算法没有仔细研究可以自行参考check_if_pq_applicable函数
至少和下面有关
1、是否能够在内存中完成
2、排序行数
3、字段数
最后需要说明一点PQ排序关闭了一次访问排序的pack功能如下:
/*
For PQ queries (with limit) we know exactly how many pointers/records
we have in the buffer, so to simplify things, we initialize
all pointers here. (We cannot pack fields anyways, so there is no
point in doing lazy initialization).
*/
五、实现代码,维护方法列出了2种实现,方法2是算法导论上的更容易理解
</n,也是达到同样的效果,同时limit也能做到分页查询如
在MYSQL官方文档中描述limit是在结果集中返回你需要的数据,它可以尽快的返回需要的行而不用管剩下的行,
在ORACLE中也有相关的语法比如 12C以前的rownun<n,也是达到同样的效果,同时limit也能做到分页查询如
limit n,m 则代表返回n开始的m行,ORACLE 12C以前也有分页方式但是相对比较麻烦
那么如果涉及到排序呢?我们需要返回按照字段排序后的某几行:
MYSQL:
select * from test order by id limit 51,100
ORACLE 12C以前:
SELECT *
FROM (SELECT tt.*, ROWNUM AS rowno
FROM (SELECT t.*
FROM test t)
ORDER BY id desc) tt
WHERE ROWNUM <= 100) table_alias
WHERE table_alias.rowno > 50;
当然如上的语法如果id列有索引那么就简单了,索引本生就是排序好的,使用索引结构即可,但是如果id列没有索引呢?
那该如何完成,难道把id列全部排序好在返回需要的行?显然这样代价过高,违背了limit中尽快返回需要的行的精神
这样我们必须使用一种合适的算法来完成,那这里就引入的堆排序和优先队列(Priority Queue 简称PQ)。
在MYSQL中执行计划没有完全的表现,执行计划依然为filesort:
mysql> explain select * from testshared3 order by id limit 10,20;
+----+-------------+-------------+------------+------+---------------+------+---------+------+---------+----------+----------------+
| id | select_type | table | partitions | type | possible_keys | key | key_len | ref | rows | filtered | Extra |
+----+-------------+-------------+------------+------+---------------+------+---------+------+---------+----------+----------------+
| 1 | SIMPLE | testshared3 | NULL | ALL | NULL | NULL | NULL | NULL | 1023820 | 100.00 | Using filesort |
+----+-------------+-------------+------------+------+---------------+------+---------+------+---------+----------+----------------+
1 row in set, 1 warning (0.02 sec)
但是根据源码的提示
DBUG_PRINT("info", ("filesort PQ is applicable"));
DBUG_PRINT("info", ("filesort PQ is not applicable"));
注意这里PQ可能弃用,什么时候弃用看后面
可以看到是否启用了PQ也就是优先队列的简写
可以再trace中找到相关说明:
[root@testmy tmp]# cat pq.trace |grep "filesort PQ is applicable"
T@2: | | | | | | | | | | info: filesort PQ is applicable
在ORACLE中使用执行计划:
--------------------------------------------------------------------------------
Plan hash value: 1473139430
--------------------------------------------------------------------------------
| Id | Operation | Name | Rows | Bytes |TempSpc| Cost (%CPU)|
--------------------------------------------------------------------------------
| 0 | SELECT STATEMENT | | 100 | 77900 | | 85431 (1)|
|* 1 | VIEW | | 100 | 77900 | | 85431 (1)|
|* 2 | COUNT STOPKEY | | | | | |
| 3 | VIEW | | 718K| 524M| | 85431 (1)|
|* 4 | SORT ORDER BY STOPKEY| | 718K| 325M| 431M| 85431 (1)|
| 5 | TABLE ACCESS FULL | TEST10 | 718K| 325M| | 13078 (1)|
这里SORT ORDER BY STOPKEY就代表了排序停止,但是ORACLE没有源码没法确切的证据使用了
优先队列和堆排序,只能猜测他使用了优先队列和堆排序
二、堆排序和优先队列
--大顶堆特性(小顶堆相似见代码)
1、必须满足完全二叉树
关于完全二叉树参考
http://blog.itpub.net/7728585/viewspace-2125889/
2、很方便的根据父节点的位置计算出两个叶子结点的位置
如果父节点的位置为i/2
左子节点为 i,右子节点为i+1
这是完全二叉树的特性决定
3、所有子节点都可以看做一个子堆那么所有结点都有
父节点>=左子节点 && 父节点>=右节点
4、很明显的可以找到最大的元素,就是整个堆的根结点
--堆需要完成操作
堆排序方法也是最优队列的实现方法,MYSQL源码中明显的使用了优先队列来优化order by limit n ,估计max也是用的这种算法
当然前提是没有使用到索引的情况下。
根据这些特性明显又是一个递归的成堆的操作。
参考算法导论第六章,里面的插图能够加深理解,这里截取一张构建好的大顶堆

构建方法:自下而上的构建自左向右构建堆,其实就是不断调用维护方法的过程
维护方法:使用递归的逐级下降的方法进行维护,是整个算法的核心内容,搞清楚了维护方法其他任何操作都来自于它。
排序方法:最大元素放到最后,然后逐层下降的方法进行调整。
数据库中的应用:
order by asc/desc limit n:简化的排序而已,只是排序前面n就可以了,不用全部排序完成,性能优越,数据库分页查询大量使用这个算法。参考代码
max/min :a[1]就是最大值,只能保证a[1]>=a[2]&&a[1]>=a[3] 不能保证a[3]>=a[4],堆建立完成后就可以找到MAX值,但是MYSQL max并没有使用这个算法
我在代码中完成了这些操作,代码中有比较详细的注释,这里就不详细说明了。
我使用了2个数组用于作为测试数据
int i,a[11]={0,999,3,2,9,34,5,102,90,2222,1}; //测试数据 a[0]不使用
int b[11]={0,999,3,2,9,999,888888,102,90,2222,111};//测试数据 b[0]不使用
分别求a素组的最大值和最小前3位数字,求b数组的MAX/MIN值,结果如下:
gaopeng@bogon:~/datas$ ./a.out
大顶堆:
order by desc a array limit 3 result:2222 999 102
max values b array reulst:888888
小顶堆:
order by asc a array limit 3 result:1 2 3
min values b array reulst:2
可以看到没问题。
--优先队列:优先队列不同于普通队列先进先出的规则,而定义为以某种规定先出,比如最大先出或者最小先出,这个没什么难度了,不就和数据库的order
by limit是一回事吗?当然是用大顶堆或者小顶堆完成
三、MYSQL中优先队列的接口
MYSQL中的优先队列类在
priority_queue.h中的class Priority_queue : public Less
他实现了很多功能,不过其他功能都很简单主要是堆的维护
下面是MYSQL源码中的堆的维护代码
void heapify(size_type i, size_type last)
{
DBUG_ASSERT(i < size());
size_type largest = i;
do
{
i = largest;
size_type l = left(i);
size_type r = right(i);
if (l < last && Base::operator()(m_container[i], m_container[l]))
{
largest = l;
}
if (r < last && Base::operator()(m_container[largest], m_container[r]))
{
largest = r;
}
if (largest != i)
{
std::swap(m_container[i], m_container[largest]);
}
} while (largest != i);
}
可以看见实际和我写的差不多。
四、MYSQL如何判断是否启用PQ
一般来说快速排序的效率高于堆排序,但是堆排序有着天生的特点可以实现优先队列,来实现
order by limit
(关于快速排序参考:http://blog.itpub.net/7728585/viewspace-2130743/)
那么这里就涉及一个问题,那就是快速排序和最优的队列的临界切换,比如
表A 100W行记录 id列没有索引
select * from a order by id limit 10;
和
select * from a order by id limit 900000,10;
肯定前者应该使用最优队列,而后者实际上要排序好至少900010行数据才能返回。
那么这个时候应该使用快速排序,那么trace信息应该为
filesort PQ is not applicable
[root@testmy tmp]# cat pqdis.trace |grep "filesort PQ "
T@2: | | | | | | | | | | info: filesort PQ is not applicable
那么MYSQL值确定是否使用PQ,其判定接口为check_if_pq_applicable函数,
简单的说MYSQL认为堆排序比快速排序慢3倍如下:
/*
How much Priority Queue sort is slower than qsort.
Measurements (see unit test) indicate that PQ is roughly 3 times slower.
*/
const double PQ_slowness= 3.0;
所以就要进行算法的切换,但是具体算法没有仔细研究可以自行参考check_if_pq_applicable函数
至少和下面有关
1、是否能够在内存中完成
2、排序行数
3、字段数
最后需要说明一点PQ排序关闭了一次访问排序的pack功能如下:
/*
For PQ queries (with limit) we know exactly how many pointers/records
we have in the buffer, so to simplify things, we initialize
all pointers here. (We cannot pack fields anyways, so there is no
point in doing lazy initialization).
*/
五、实现代码,维护方法列出了2种实现,方法2是算法导论上的更容易理解
点击(此处)折叠或打开
-
/*************************************************************************
-
> File Name: heapsort.c
-
> Author: gaopeng QQ:22389860 all right reserved
-
> Mail: gaopp_200217@163.com
-
> Created Time: Sun 08 Jan 2017 11:22:14 PM CST
-
************************************************************************/
-
-
#include<stdio.h>
-
#include<stdlib.h>
-
-
#define LEFT(i) i<<1
-
#define RIGTH(i) (i<<1)+1
-
//堆排序的性能不及快速排序但是在某些情况下非常有用
-
//数据库的order by limit使用了优先队列,基于堆排序
-
-
int swap(int k[],int i,int j)
-
{
-
int temp;
-
-
temp = k[i];
-
k[i] = k[j];
-
k[j] = temp;
- return 0;
-
}
-
-
-
int bigheapad(int k[],int s,int n) //s=4,n=9
-
{
-
/*
-
* one:
-
int i;
-
int temp = k[s]; //temp=9=k[4] 父节点值保存到temp
-
for(i=2*s;i<=n;i=i*2)// i=8
-
{
-
if(i<n && k[i]<k[i+1])//如果左子节点小于右子节点
-
{
-
i++; //右节点
-
}
-
-
if(temp>=k[i])
-
{
-
break;
-
}
-
-
k[s] = k[i];
-
s = i;
-
}
-
-
k[s] = temp;
-
*/
-
// two: 参考算法导论P155页,整个方法更容易理解其原理,调整使用逐层下降的方法进行调整
-
int l; //s 左节点编号
-
int r; //s 右节点编号
-
int largest;
-
-
l=LEFT(s); //左节点编号
-
r=RIGTH(s);//右节点编号
-
-
if(s<=n/2) // n/2为最小节点编号的父亲节点 如果s大于这个值说明这个节点不会有任何子节点不需要进行调整 !!,这是整个算法的核心中的核心。搞了我老半天
-
{
-
if (l<=n && k[l] > k[s])
-
{
-
largest = l;
-
}
-
else
-
{
-
largest = s;
-
}
-
-
if(r<=n && k[r] > k[largest])
-
{
-
largest = r;
-
}
-
-
if(largest != s)
-
{
-
swap(k,largest,s);
-
bigheapad(k,largest,n); //对数据调整后可能的子节点树继续进行调整直到达到递归退出条件
-
}
-
}
- return 0;
-
}
-
-
-
int bigheapbulid(int k[],int n)
-
{
-
int i;
-
for(i=n/2;i>0;i--)//采用自底向上的方法构建 算法导论P156 EXP 1:i= n/2 p:4 l:8 r:9 2: i = p:3 l:6 r:7 n/2刚好是最后一个节点的父亲节点所以自下而上
-
{
-
bigheapad(k,i,n);
-
}
- return 0;
-
-
}
-
-
int bigheapsort(int k[],int n) //sort的过程就是将最大元素放到最后,然后逐层下降的方法进行调整
-
{
-
int i;
-
for(i=n;i>1;i--)
-
{
-
swap(k,1,i);
-
bigheapad(k,1,i-1);
-
}
- return 0;
-
}
-
- int biglimitn(int k[],int n,int limitn)//limit 也是我关心的 这里明显可以看到他的优势实际它不需要对整个数组排序,你要多少我排多少给你就好,也是最大元素放到最后,然后逐层下降的方法进行调整的原理
-
{
-
int i;
-
for(i=n;i>n-limitn;i--)
-
{
-
swap(k,1,i);
-
bigheapad(k,1,i-1);
-
}
- return 0;
-
}
-
-
int smallheapad(int k[],int s,int n) //s=4,n=9
-
{
-
-
int l; //s 左节点编号
-
int r; //s 右节点编号
-
int smallest;
-
-
l=LEFT(s); //左节点编号
-
r=RIGTH(s);//右节点编号
-
-
if(s<=n/2) // n/2为最小节点编号的父亲节点 如果s大于这个值说明这个节点不会有任何子节点不需要进行调整 !!
-
{
-
-
if (l<=n && k[l] < k[s])
-
{
-
-
smallest = l;
-
}
-
else
-
{
-
-
smallest = s;
-
}
-
-
if(r<=n && k[r] < k[smallest])
-
{
-
-
smallest = r;
-
}
-
-
if(smallest != s)
-
{
-
-
swap(k,smallest,s);
-
smallheapad(k,smallest,n); //对数据调整后可能的子节点树继续进行调整直到达到递归退出条件
-
}
-
}
- return 0;
-
}
-
-
-
int smallheapbulid(int k[],int n)
-
{
-
-
int i;
-
for(i=n/2;i>0;i--)
-
{
-
-
smallheapad(k,i,n);
-
}
- return 0;
-
}
-
-
int smallheapsort(int k[],int n)
-
{
-
-
int i;
-
for(i=n;i>1;i--)
-
{
-
-
swap(k,1,i);
-
smallheapad(k,1,i-1);
-
}
-
return 0;
-
}
-
-
int smalllimitn(int k[],int n,int limitn)
-
{
-
-
int i;
-
for(i=n;i>n-limitn;i--)
-
{
-
-
swap(k,1,i);
-
smallheapad(k,1,i-1);
-
}
- return 0;
-
}
-
-
-
int main()
-
{
-
-
int i,a[11]={0,999,3,2,9,34,5,102,90,2222,1}; //测试数据 a[0]不使用
-
int b[11]={0,999,3,2,9,999,888888,102,90,2222,111};//测试数据 b[0]不使用
-
bigheapbulid(a,10);
-
biglimitn(a,10,3);
-
-
printf("大顶堆:/n");
-
printf("order by desc a array limit 3 result:");
-
for(i=10;i>10-3;i--)
-
{
-
printf("%d ",a[i]);
-
}
-
printf("/n");
-
bigheapbulid(b,10);
-
printf("max values b array reulst:");
-
printf("%d /n",b[1]);
-
-
smallheapbulid(a,10);
-
smalllimitn(a,10,3);
-
printf("小顶堆:/n");
-
printf("order by asc a array limit 3 result:");
-
for(i=10;i>10-3;i--)
-
{
-
printf("%d ",a[i]);
-
}
-
printf("/n");
-
smallheapbulid(b,10);
-
printf("min values b array reulst:");
-
printf("%d /n",b[1]);
- return 0;
- }
</n,也是达到同样的效果,同时limit也能做到分页查询如
正文到此结束
热门推荐
相关文章
Loading...











![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)

