大话分布式系统理论基础（上）

分布式系统理论基础 - 一致性、2PC和3PC

引言

狭义的分布式系统指由网络连接的计算机系统，每个节点独立地承担计算或存储任务，节点间通过网络协同工作。广义的分布式系统是一个相对的概念，正如 所说[1]：

What is a distributed systeme. Distribution is in the eye of the beholder.
To the user sitting at the keyboard, his IBM personal computer is a nondistributed system. 
To a flea crawling around on the circuit board, or to the engineer who designed it, it's very much a distributed system.

一致性是分布式理论中的根本性问题，近半个世纪以来，科学家们围绕着一致性问题提出了很多理论模型，依据这些理论模型，业界也出现了很多工程实践投影。下面我们从一致性问题、特定条件下解决一致性问题的两种方法(2PC、3PC)入门，了解最基础的分布式系统理论。

一致性(consensus)

何为一致性问题？简单而言，一致性问题就是相互独立的节点之间如何达成一项决议的问题。分布式系统中，进行数据库事务提交(commit transaction)、Leader选举、序列号生成等都会遇到一致性问题。这个问题在我们的日常生活中也很常见，比如牌友怎么商定几点在哪打几圈麻将：

《赌圣》，1990

假设一个具有N个节点的分布式系统，当其满足以下条件时，我们说这个系统满足一致性：

1. 全认同(agreement): 所有N个节点都认同一个结果

2. 值合法(validity): 该结果必须由N个节点中的节点提出

3. 可结束(termination): 决议过程在一定时间内结束，不会无休止地进行下去

有人可能会说，决定什么时候在哪搓搓麻将，4个人商量一下就ok，这不很简单吗？

但就这样看似简单的事情，分布式系统实现起来并不轻松，因为它面临着这些问题：

• 消息传递异步无序(asynchronous): 现实网络不是一个可靠的信道，存在消息延时、丢失，节点间消息传递做不到同步有序(synchronous)

• 节点宕机(fail-stop): 节点持续宕机，不会恢复

• 节点宕机恢复(fail-recover): 节点宕机一段时间后恢复，在分布式系统中最常见

• 网络分化(network partition): 网络链路出现问题，将N个节点隔离成多个部分

• 拜占庭将军问题(byzantine failure)[2]: 节点或宕机或逻辑失败，甚至不按套路出牌抛出干扰决议的信息

假设现实场景中也存在这样的问题，我们看看结果会怎样：

还能不能一起愉快地玩耍...

我们把以上所列的问题称为系统模型(system model)，讨论分布式系统理论和工程实践的时候，必先划定模型。例如有以下两种模型：

1. 异步环境(asynchronous)下，节点宕机(fail-stop)

2. 异步环境(asynchronous)下，节点宕机恢复(fail-recover)、网络分化(network partition)

2比1多了节点恢复、网络分化的考量，因而对这两种模型的理论研究和工程解决方案必定是不同的，在还没有明晰所要解决的问题前谈解决方案都是一本正经地耍流氓。

一致性还具备两个属性，一个是强一致(safety)，它要求所有节点状态一致、共进退；一个是可用(liveness)，它要求分布式系统24*7无间断对外服务。FLP定理(FLP impossibility)[3][4] 已经证明在一个收窄的模型中(异步环境并只存在节点宕机)，不能同时满足 safety 和 liveness。

FLP定理是分布式系统理论中的基础理论，正如物理学中的能量守恒定律彻底否定了永动机的存在，FLP定理否定了同时满足safety 和 liveness 的一致性协议的存在。

《怦然心动 (Flipped)》，2010

工程实践上根据具体的业务场景，或保证强一致(safety)，或在节点宕机、网络分化的时候保证可用(liveness)。2PC、3PC是相对简单的解决一致性问题的协议，下面我们就来了解2PC和3PC。

2PC

2PC(tow phase commit)两阶段提交[5]顾名思义它分成两个阶段，先由一方进行提议(propose)并收集其他节点的反馈(vote)，再根据反馈决定提交(commit)或中止(abort)事务。我们将提议的节点称为协调者(coordinator)，其他参与决议节点称为参与者(participants, 或cohorts)：

2PC, phase one

在阶段1中，coordinator发起一个提议，分别问询各participant是否接受。

2PC, phase two

在阶段2中，coordinator根据participant的反馈，提交或中止事务，如果participant全部同意则提交，只要有一个participant不同意就中止。

在异步环境(asynchronous)并且没有节点宕机(fail-stop)的模型下，2PC可以满足全认同、值合法、可结束，是解决一致性问题的一种协议。但如果再加上节点宕机(fail-recover)的考虑，2PC是否还能解决一致性问题呢？

coordinator如果在发起提议后宕机，那么participant将进入阻塞(block)状态、一直等待coordinator回应以完成该次决议。这时需要另一角色把系统从不可结束的状态中带出来，我们把新增的这一角色叫协调者备份(coordinator watchdog)。coordinator宕机一定时间后，watchdog接替原coordinator工作，通过问询(query) 各participant的状态，决定阶段2是提交还是中止。这也要求 coordinator/participant 记录(logging)历史状态，以备coordinator宕机后watchdog对participant查询、coordinator宕机恢复后重新找回状态。

从coordinator接收到一次事务请求、发起提议到事务完成，经过2PC协议后增加了2次RTT(propose+commit)，带来的时延(latency)增加相对较少。

3PC

3PC(three phase commit)即三阶段提交[6][7]，既然2PC可以在异步网络+节点宕机恢复的模型下实现一致性，那还需要3PC做什么，3PC是什么鬼？

在2PC中一个participant的状态只有它自己和coordinator知晓，假如coordinator提议后自身宕机，在watchdog启用前一个participant又宕机，其他participant就会进入既不能回滚、又不能强制commit的阻塞状态，直到participant宕机恢复。这引出两个疑问：

1. 能不能去掉阻塞，使系统可以在commit/abort前回滚(rollback)到决议发起前的初始状态

2. 当次决议中，participant间能不能相互知道对方的状态，又或者participant间根本不依赖对方的状态

相比2PC，3PC增加了一个准备提交(prepare to commit)阶段来解决以上问题：

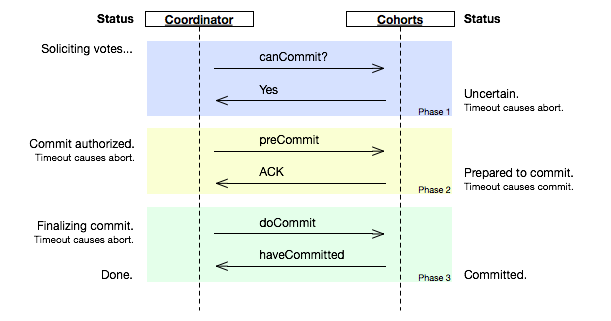
图片截取自wikipedia

coordinator接收完participant的反馈(vote)之后，进入阶段2，给各个participant发送准备提交(prepare to commit)指令。participant接到准备提交指令后可以锁资源，但要求相关操作必须可回滚。coordinator接收完确认(ACK)后进入阶段3、进行commit/abort，3PC的阶段3与2PC的阶段2无异。协调者备份(coordinator watchdog)、状态记录(logging)同样应用在3PC。

Participant如果在不同阶段宕机，我们来看看3PC如何应对：

• 阶段1: coordinator或watchdog未收到宕机participant的vote，直接中止事务；宕机的participant恢复后，读取logging发现未发出赞成vote，自行中止该次事务

• 阶段2: coordinator未收到宕机participant的precommit ACK，但因为之前已经收到了宕机participant的赞成反馈(不然也不会进入到阶段2)，coordinator进行commit；watchdog可以通过问询其他participant获得这些信息，过程同理；宕机的participant恢复后发现收到precommit或已经发出赞成vote，则自行commit该次事务

• 阶段3: 即便coordinator或watchdog未收到宕机participant的commit ACK，也结束该次事务；宕机的participant恢复后发现收到commit或者precommit，也将自行commit该次事务

因为有了准备提交(prepare to commit)阶段，3PC的事务处理延时也增加了1个RTT，变为3个RTT(propose+precommit+commit)，但是它防止participant宕机后整个系统进入阻塞态，增强了系统的可用性，对一些现实业务场景是非常值得的。

小结

以上介绍了分布式系统理论中的部分基础知识，阐述了一致性(consensus)的定义和实现一致性所要面临的问题，最后讨论在异步网络(asynchronous)、节点宕机恢复(fail-recover)模型下2PC、3PC怎么解决一致性问题。

阅读前人对分布式系统的各项理论研究，其中有严谨地推理、证明，有一种数学的美；观现实中的分布式系统实现，是综合各种因素下妥协的结果。

[1]  Solved Problems, Unsolved Problems and Problems in Concurrency , Leslie Lamport, 1983

[2]  The Byzantine Generals Problem , Leslie Lamport,Robert Shostak and Marshall Pease, 1982

[3]  Impossibility of Distributed Consensus with One Faulty Process , Fischer, Lynch and Patterson, 1985

[4]  FLP Impossibility的证明 , Daniel Wu, 2015

[5]  Consensus Protocols: Two-Phase Commit , Henry Robinson, 2008

[6]  Consensus Protocols: Three-phase Commit , Henry Robinson, 2008

[7]  Three-phase commit protocol , Wikipedia

分布式系统理论基础 - CAP

引言

CAP是分布式系统、特别是分布式存储领域中被讨论最多的理论，“ ”在Quora 分布式系统分类下排名 FAQ 的 No.1。CAP在程序员中也有较广的普及，它不仅仅是“C、A、P不能同时满足，最多只能3选2”，以下尝试综合各方观点，从发展历史、工程实践等角度讲述CAP理论。希望大家透过本文对CAP理论有更多地了解和认识。

CAP定理

CAP由 在2000年PODC会议上提出[1][2]，是Eric Brewer在Inktomi[3]期间研发搜索引擎、分布式web缓存时得出的关于数据一致性(consistency)、服务可用性(availability)、分区容错性(partition-tolerance)的猜想：

It is impossible for a web service to provide the three following guarantees : Consistency, Availability and Partition-tolerance.

该猜想在提出两年后被证明成立[4]，成为我们熟知的CAP定理：

• 数据一致性(consistency)：如果系统对一个写操作返回成功，那么之后的读请求都必须读到这个新数据；如果返回失败，那么所有读操作都不能读到这个数据，对调用者而言数据具有强一致性(strong consistency) (又叫原子性 atomic、线性一致性 linearizable consistency)[5]

• 服务可用性(availability)：所有读写请求在一定时间内得到响应，可终止、不会一直等待

• 分区容错性(partition-tolerance)：在网络分区的情况下，被分隔的节点仍能正常对外服务

在某时刻如果满足AP，分隔的节点同时对外服务但不能相互通信，将导致状态不一致，即不能满足C；如果满足CP，网络分区的情况下为达成C，请求只能一直等待，即不满足A；如果要满足CA，在一定时间内要达到节点状态一致，要求不能出现网络分区，则不能满足P。

C、A、P三者最多只能满足其中两个，和FLP定理一样，CAP定理也指示了一个不可达的结果(impossibility result)。

CAP的工程启示

CAP理论提出7、8年后，NoSql圈将CAP理论当作对抗传统关系型数据库的依据、阐明自己放宽对数据一致性(consistency)要求的正确性[6]，随后引起了大范围关于CAP理论的讨论。

CAP理论看似给我们出了一道3选2的选择题，但在工程实践中存在很多现实限制条件，需要我们做更多地考量与权衡，避免进入CAP认识误区[7]。

1、关于 P 的理解

Partition字面意思是网络分区，即因网络因素将系统分隔为多个单独的部分，有人可能会说，网络分区的情况发生概率非常小啊，是不是不用考虑P，保证CA就好[8]。要理解P，我们看回CAP证明[4]中P的定义：

In order to model partition tolerance, the network will be allowed to lose arbitrarily many messages sent from one node to another.

网络分区的情况符合该定义，网络丢包的情况也符合以上定义，另外节点宕机，其他节点发往宕机节点的包也将丢失，这种情况同样符合定义。现实情况下我们面对的是一个不可靠的网络、有一定概率宕机的设备，这两个因素都会导致Partition，因而分布式系统实现中 P 是一个必须项，而不是可选项[9][10]。

对于分布式系统工程实践，CAP理论更合适的描述是：在满足分区容错的前提下，没有算法能同时满足数据一致性和服务可用性[11]：

In a network subject to communication failures, it is impossible for any web service to implement an atomic read/write shared memory that guarantees a response to every request.

2、CA非0/1的选择

P 是必选项，那3选2的选择题不就变成数据一致性(consistency)、服务可用性(availability) 2选1？工程实践中一致性有不同程度，可用性也有不同等级，在保证分区容错性的前提下，放宽约束后可以兼顾一致性和可用性，两者不是非此即彼[12]。

CAP定理证明中的一致性指强一致性，强一致性要求多节点组成的被调要能像单节点一样运作、操作具备原子性，数据在时间、时序上都有要求。如果放宽这些要求，还有其他一致性类型：

• 序列一致性(sequential consistency)[13]：不要求时序一致，A操作先于B操作，在B操作后如果所有调用端读操作得到A操作的结果，满足序列一致性

• 最终一致性(eventual consistency)[14]：放宽对时间的要求，在被调完成操作响应后的某个时间点，被调多个节点的数据最终达成一致

可用性在CAP定理里指所有读写操作必须要能终止，实际应用中从主调、被调两个不同的视角，可用性具有不同的含义。当P(网络分区)出现时，主调可以只支持读操作，通过牺牲部分可用性达成数据一致。

工程实践中，较常见的做法是通过异步拷贝副本(asynchronous replication)、quorum/NRW，实现在调用端看来数据强一致、被调端最终一致，在调用端看来服务可用、被调端允许部分节点不可用(或被网络分隔)的效果[15]。

3、跳出CAP

CAP理论对实现分布式系统具有指导意义，但CAP理论并没有涵盖分布式工程实践中的所有重要因素。

例如延时(latency)，它是衡量系统可用性、与用户体验直接相关的一项重要指标[16]。CAP理论中的可用性要求操作能终止、不无休止地进行，除此之外，我们还关心到底需要多长时间能结束操作，这就是延时，它值得我们设计、实现分布式系统时单列出来考虑。

延时与数据一致性也是一对“冤家”，如果要达到强一致性、多个副本数据一致，必然增加延时。加上延时的考量，我们得到一个CAP理论的修改版本PACELC[17]：如果出现P(网络分区)，如何在A(服务可用性)、C(数据一致性)之间选择；否则，如何在L(延时)、C(数据一致性)之间选择。

小结

以上介绍了CAP理论的源起和发展，介绍了CAP理论给分布式系统工程实践带来的启示。

CAP理论对分布式系统实现有非常重大的影响，我们可以根据自身的业务特点，在数据一致性和服务可用性之间作出倾向性地选择。通过放松约束条件，我们可以实现在不同时间点满足CAP(此CAP非CAP定理中的CAP，如C替换为最终一致性)[18][19][20]。

有非常非常多文章讨论和研究CAP理论，希望这篇对你认识和了解CAP理论有帮助。

[1]  Harvest, Yield, and Scalable Tolerant Systems , Armando Fox , Eric Brewer, 1999

[2]  Towards Robust Distributed Systems , Eric Brewer, 2000

[3]  Inktomi's wild ride - A personal view of the Internet bubble , Eric Brewer, 2004

[4]  Brewer’s Conjecture and the Feasibility of Consistent, Available, Partition-Tolerant Web , Seth Gilbert, Nancy Lynch, 2002

[5]  Linearizability: A Correctness Condition for Concurrent Objects , Maurice P. Herlihy,Jeannette M. Wing, 1990

[6]  Brewer's CAP Theorem - The kool aid Amazon and Ebay have been drinking , Julian Browne, 2009

[7]  CAP Theorem between Claims and Misunderstandings: What is to be Sacrificed? , Balla Wade Diack,Samba Ndiaye,Yahya Slimani, 2013

[8]  Errors in Database Systems, Eventual Consistency, and the CAP Theorem , Michael Stonebraker, 2010

[9]  CAP Confusion: Problems with 'partition tolerance' , Henry Robinson, 2010

[10]  You Can’t Sacrifice Partition Tolerance , Coda Hale, 2010

[11]  Perspectives on the CAP Theorem , Seth Gilbert, Nancy Lynch, 2012

[12]  CAP Twelve Years Later: How the "Rules" Have Changed , Eric Brewer, 2012

[13]  How to Make a Multiprocessor Computer That Correctly Executes Multiprocess Programs , Lamport Leslie, 1979

[14]  Eventual Consistent Databases: State of the Art , Mawahib Elbushra , Jan Lindström, 2014

[15]  Eventually Consistent , Werner Vogels, 2008

[16]  Speed Matters for Google Web Search , Jake Brutlag, 2009

[17]  Consistency Tradeoffs in Modern Distributed Database System Design , Daniel J. Abadi, 2012

[18]  A CAP Solution (Proving Brewer Wrong) , Guy's blog, 2008

[19]  How to beat the CAP theorem , nathanmarz , 2011

[20]  , Henry Robinson

分布式系统理论基础 - 时间、时钟和事件顺序

十六号…… 四月十六号。一九六零年四月十六号下午三点之前的一分钟你和我在一起，因为你我会记住这一分钟。从现在开始我们就是一分钟的朋友，这是事实，你改变不了，因为已经过去了。我明天会再来。

—— 《阿飞正传》

现实生活中时间是很重要的概念，时间可以记录事情发生的时刻、比较事情发生的先后顺序。分布式系统的一些场景也需要记录和比较不同节点间事件发生的顺序，但不同于日常生活使用物理时钟记录时间，分布式系统使用逻辑时钟记录事件顺序关系，下面我们来看分布式系统中几种常见的逻辑时钟。

物理时钟 vs 逻辑时钟

可能有人会问，为什么分布式系统不使用物理时钟(physical clock)记录事件？每个事件对应打上一个时间戳，当需要比较顺序的时候比较相应时间戳就好了。

这是因为现实生活中物理时间有统一的标准，而分布式系统中每个节点记录的时间并不一样，即使设置了   时间同步节点间也存在毫秒级别的偏差[1][2]。因而分布式系统需要有另外的方法记录事件顺序关系，这就是逻辑时钟(logical clock)。

Lamport timestamps

在1978年提出逻辑时钟的概念，并描述了一种逻辑时钟的表示方法，这个方法被称为Lamport时间戳(Lamport timestamps)[3]。

分布式系统中按是否存在节点交互可分为三类事件，一类发生于节点内部，二是发送事件，三是接收事件。Lamport时间戳原理如下：

图1: Lamport timestamps space time (图片来源: wikipedia)

1. 每个事件对应一个Lamport时间戳，初始值为0

2. 如果事件在节点内发生，时间戳加1

3. 如果事件属于发送事件，时间戳加1并在消息中带上该时间戳

4. 如果事件属于接收事件，时间戳 = Max(本地时间戳，消息中的时间戳) + 1

假设有事件a、b，C(a)、C(b)分别表示事件a、b对应的Lamport时间戳，如果C(a) < C(b)，则有a发生在b之前(happened before)，记作 a -> b，例如图1中有 C1 -> B1。通过该定义，事件集中Lamport时间戳不等的事件可进行比较，我们获得事件的 (partial order)。

如果C(a) = C(b)，那a、b事件的顺序又是怎样的？假设a、b分别在节点P、Q上发生，Pi、Qj分别表示我们给P、Q的编号，如果 C(a) = C(b) 并且 Pi < Qj，同样定义为a发生在b之前，记作 a => b。假如我们对图1的A、B、C分别编号Ai = 1、Bj = 2、Ck = 3，因 C(B4) = C(C3) 并且 Bj < Ck，则 B4 => C3。

通过以上定义，我们可以对所有事件排序、获得事件的 (total order)。上图例子，我们可以从C1到A4进行排序。

Vector clock

Lamport时间戳帮助我们得到事件顺序关系，但还有一种顺序关系不能用Lamport时间戳很好地表示出来，那就是同时发生关系(concurrent)[4]。例如图1中事件B4和事件C3没有因果关系，属于同时发生事件，但Lamport时间戳定义两者有先后顺序。

Vector clock是在Lamport时间戳基础上演进的另一种逻辑时钟方法，它通过vector结构不但记录本节点的Lamport时间戳，同时也记录了其他节点的Lamport时间戳[5][6]。Vector clock的原理与Lamport时间戳类似，使用图例如下：

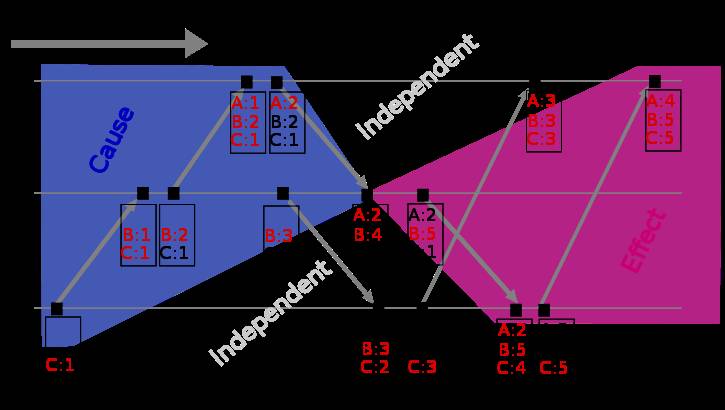
图2: Vector clock space time (图片来源: wikipedia)

假设有事件a、b分别在节点P、Q上发生，Vector clock分别为Ta、Tb，如果 Tb[Q] > Ta[Q] 并且 Tb[P] >= Ta[P]，则a发生于b之前，记作 a -> b。到目前为止还和Lamport时间戳差别不大，那Vector clock怎么判别同时发生关系呢？

如果 Tb[Q] > Ta[Q] 并且 Tb[P] < Ta[P]，则认为a、b同时发生，记作 a <-> b。例如图2中节点B上的第4个事件 (A:2，B:4，C:1) 与节点C上的第2个事件 (B:3，C:2) 没有因果关系、属于同时发生事件。

Version vector

基于Vector clock我们可以获得任意两个事件的顺序关系，结果或为先后顺序或为同时发生，识别事件顺序在工程实践中有很重要的引申应用，最常见的应用是发现数据冲突(detect conflict)。

分布式系统中数据一般存在多个副本(replication)，多个副本可能被同时更新，这会引起副本间数据不一致[7]，Version vector的实现与Vector clock非常类似[8]，目的用于发现数据冲突[9]。下面通过一个例子说明Version vector的用法[10]：

图3: Version vector

• client端写入数据，该请求被Sx处理并创建相应的vector ([Sx, 1])，记为数据D1

• 第2次请求也被Sx处理，数据修改为D2，vector修改为([Sx, 2])

• 第3、第4次请求分别被Sy、Sz处理，client端先读取到D2，然后D3、D4被写入Sy、Sz

• 第5次更新时client端读取到D2、D3和D4 3个数据版本，通过类似Vector clock判断同时发生关系的方法可判断D3、D4存在数据冲突，最终通过一定方法解决数据冲突并写入D5

Vector clock只用于发现数据冲突，不能解决数据冲突。如何解决数据冲突因场景而异，具体方法有以最后更新为准(last write win)，或将冲突的数据交给client由client端决定如何处理，或通过quorum决议事先避免数据冲突的情况发生[11]。

由于记录了所有数据在所有节点上的逻辑时钟信息，Vector clock和Version vector在实际应用中可能面临的一个问题是vector过大，用于数据管理的元数据(meta data)甚至大于数据本身[12]。

解决该问题的方法是使用server id取代client id创建vector (因为server的数量相对client稳定)，或设定最大的size、如果超过该size值则淘汰最旧的vector信息[10][13]。

小结

以上介绍了分布式系统里逻辑时钟的表示方法，通过Lamport timestamps可以建立事件的全序关系，通过Vector clock可以比较任意两个事件的顺序关系并且能表示无因果关系的事件，将Vector clock的方法用于发现数据版本冲突，于是有了Version vector。

[1]  , George Neville-Neil, 2016

[2]  , Justin Sheehy, 2015

[3]  Time, Clocks, and the Ordering of Events in a Distributed System , Leslie Lamport, 1978

[4]  Timestamps in Message-Passing Systems That Preserve the Partial Ordering , Colin J. Fidge, 1988

[5]  Virtual Time and Global States of Distributed Systems , Friedemann Mattern, 1988

[6]  Why Vector Clocks are Easy , Bryan Fink, 2010

[7]  , CouchDB

[8]  Version Vectors are not Vector Clocks , Carlos Baquero, 2011

[9]  Detection of Mutual Inconsistency in Distributed Systems , IEEE Transactions on Software Engineering , 1983

[10]  Dynamo: Amazon’s Highly Available Key-value Store , Amazon, 2007

[11]  , Jeff Darcy , 2010

[12]  Why Vector Clocks Are Hard , Justin Sheehy, 2010

[13]  Causality Is Expensive (and What To Do About It) , Peter Bailis ,2014

温馨提示：

请搜索 “ICT_Architect” 或 “扫一扫” 下面二维码关注公众号，获取更多精彩内容。