转载

深入浅出朴素贝叶斯理论

深入浅出朴素贝叶斯理论归属于笔者的程序猿的数据科学与机器学习实战手册。部分阅读平台对于MathJax支持不好，可以查看笔者的笔记原文。更多内容参考面向程序猿的数据科学与机器学习知识体系及资料合集。

深入浅出朴素贝叶斯理论

概率论是机器学习中的重要角色，那么何谓概率？我们在小学里就听老师讲过抛硬币时正面朝上的概率为0.5，这句话又代表着何含义呢？对于概率的理解往往有两种不同的方式，其一是所谓的频率论解释（Frequentist Interpretation）。这种观点中，概率代表着某个事件在较长范围内的出现频次。譬如这里的抛硬币问题可以阐述为，如果我们抛足够的次数，我们会观测到正面朝上的次数与反面朝上的次数基本相同。另一种即时所谓的贝叶斯解释（Bayesian Interpretation），我们认为概率是用来衡量某件事的不确定性（uncertainty），其更多地与信息相关而不再是重复尝试的次数。用贝叶斯理论阐述抛硬币问题则为下一次抛硬币时正面朝上的可能性与反面朝上的可能性相差无几。贝叶斯解释的最大优势在于我们可以去为事件的不确定性建立具体的模型而不再依赖于多次试验得出的频次结果。譬如我们要去预测2020年世界杯的冠军，我们肯定不能让球队比赛很多次来观测频次计算概率，这件事只会发生零或一次，反正是无法重复发生的。基于贝叶斯理论我们便可以利用可观测到的数据推测该事件的结果概率，典型的应用是垃圾邮件过滤系统中，我们可以根据带标签的训练数据来对新的邮件进行判断。

朴素贝叶斯

贝叶斯定理缘起于托马斯.贝叶斯（1702-1761），一位英国长老会牧师和业余数学家。在他去世后发表的论文“论有关机遇问题的求解”中，贝叶斯定理的现代形式实际上归因于拉普拉斯（1812）。拉普拉斯重新发现了贝叶斯定理，并把它用来解决天体力学、医学甚至法学的问题。但自19世纪中叶起，随着频率学派（在下文有时也称作经典统计）的兴起，概率的贝叶斯解释逐渐被统计学主流所拒绝。现代贝叶斯统计学的复兴肇始于Jeffreys(1939),在1950年代，经过Wald(1950), Savage(1954), Raiffic&Schlaifer(1961), Lindley(1972), De Finetti(1974)等人的努力，贝叶斯统计学逐渐发展壮大，并发展出了贝叶斯统计决策理论这个新分支。特别是到1990年代以后，随着计算方法MCMC在贝叶斯统计领域的广泛应用，解决了贝叶斯统计学长期存在的计算困难的问题，从而推动了贝叶斯统计在理论和应用领域的长足发展。贝叶斯统计学广泛应用于各个学科。就本书的主题而言，从认知学科、政治学到从自然语言处理和社会网络分析，贝叶斯方法都起到了举足轻重的作用。

概述

贝叶斯定理，也称为贝叶斯法则现在是概率论教科书的重要内容。一般我们习惯于它的离散（事件）形式：

P(A_i|B) = frac{P(B|A_i)P(A_i)}{ sum{P(B|A_j)P(A_j)}} /

A的后验概率 = frac{(A的似然度 * A的先验概率)}{标准化常量}

其中

$B$称为观测变量
$A_i$称为参数/隐变量
$P(A_i)$称为先验概率，表示在对样本观测前我们关于这个问题已经具有的知识
$P(A_i|B)$称为后验概率，是在进行了新观测之后对原有知识的更新
$P(B|A_i)$称为似然。
$P(B) = sum{P(B|A_j)P(A_j)}$ 称为Evidence，即数据是由该模型得出的证据

贝叶斯定理作为一种概率计算可用于多个领域内进行概率推理。今天，我们用贝叶斯法则过滤垃圾邮件，为网站用户推荐唱片、电影和书籍。它渗透到了互联网、语言和语言处理、人工智能、机器学习、金融、天文学和物理学乃至国家安全等各个领域。这里我们选用一个简单的案例进行分析，假设有方形和圆形的两种盒子，盒子内有红、黄、白三种颜色的球。方盒有3个，每个里边有红球70只、黄球10只、白球20只；圆盒有5个，每个里边有红球20只、黄球75只、白球5只。现在先任取一个盒子，再从盒中任取一球，能不能通过求得颜色推断它最有可能取自哪个盒子？为表示方便，记方盒=A，圆盒=B，红球=R，黄球=Y，白球=W 使用贝叶斯定理进行计算：

P(A|R) = frac{P(R|A)P(A)}{P(R)} =0.118125

贝叶斯理论最基础的使用就是在分类问题中，也就是所谓的生成式分类器（Generative Classifier），其基本形式如下所示：

p(y = c | vec{x},vec{theta})

propto

p(vec{x} | y = c, vec{theta})

p(y = c | vec{theta})

在训练阶段，我们基于带有标签的训练集的辅助来寻找合适的类条件概率/似然概率$p(vec{x} | y = c, vec{theta})$，并且推导出模型参数$vec{theta}$，其定义了我们期望在某类中出现某类型数据的概率。最后在预测阶段，我们基于类条件概率/似然概率来计算数据$vec{x}$从属于各个类的后验概率，并且选择概率最大的为其预测值。

Reference

贝叶斯集锦（4）：贝叶斯统计基础
贝叶斯学习及共轭先验
理解共轭先验
2012 - Machine Learning A Probabilistic Perspective - Chapter 5 - Generative models for discrete data

贝叶斯理论思维模式

在我们孩提时代，爸妈希望教会我们某个词汇的含义时，他们首先会给我们展示很多的正例。譬如对于狗这个单词，爸妈可能会说：看那条狗狗好可爱，或者，小心狗狗。不过爸妈不会像机器一样给我们展示所谓的负例，他们不会指着一只猫说：这货不是狗，最多就是当孩子们认错的时候，父母会予以纠正。心理学家研究表明，人们可以单纯地从正例中学习概念，而不一定需要负例的介入。而这种认知单词的学习过程可以抽象概括为所谓的概念学习（Concept Learning），在某些意义上很类似于二元分类。譬如我们可以定义当$x$为某个概念C的实例时$f(x) = 1$，否则$f(x) = 0$。而学习的过程即是构建这个指示函数$f$，该函数定义了哪些元素属于概念C。当我们允许这个函数具有一定的不确定性时，我们就可以通过概率计算得出所谓的模糊集（Fuzzy Set）。还需要提到的是，标准的二维分类是同时需要正负例存在的，不过我们也可以单纯地从正例中学习。

阐述完了基本的概念，接下来我们会以一个简单的数字游戏来进行形象化的说明，这里我们随便选定几个数学上的概念作为学习目标。譬如我们可以将概念C定义为所有的素数，或者介于1~10之间的数字。然后给你多组随机从C中抽样出的正数序列：$D = {x_1,...,x_N}$，然后给你一个新的测试序列$ widetilde{x} $让你判断其应该归属于哪个概念。

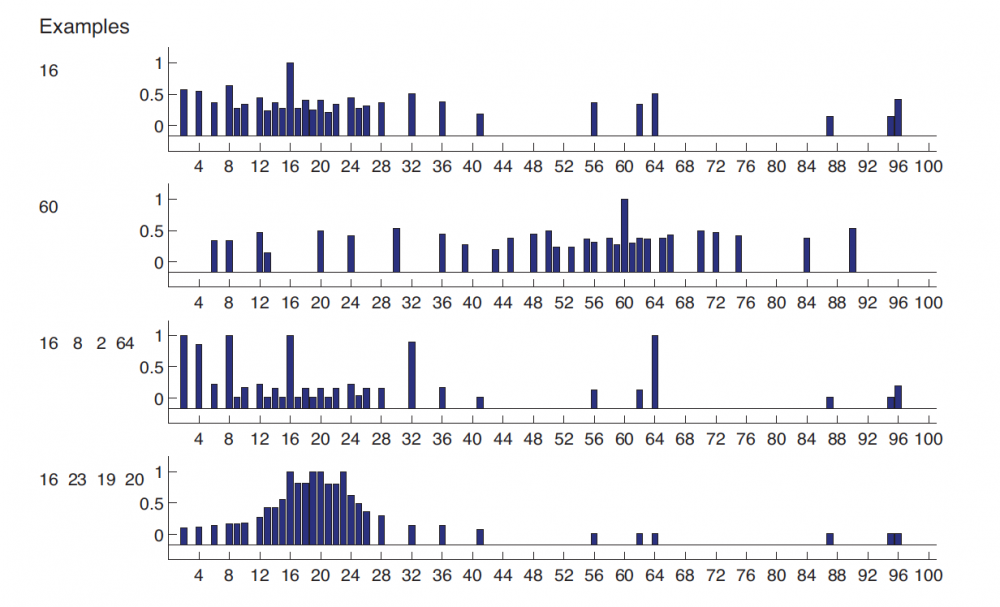
深入浅出朴素贝叶斯理论

上图四组对比数据分别显示了给不同的组选定不同的观测集合时他们推导出的概念C的数字分布。前两行是分别展示了$D = {16}$与$D = {60}$，会发现得出的结果非常分散（这里选定的数字范围为1~100）。而第三行中观测数据为$D = {16，8，2，64}$，人们得出了一定的规律，即选定了2的方幂值。而最后一行中给出的观测数据是$D = {16，23，19，20}$，人们得出的规律是选定靠近20的数字。我们来复盘每个组的思考过程，譬如当首先给出$16$作为观测数据时，人们可能会选择17？因为17离16最近，也有可能会选择6，因为它们的个位数都是6.当然也有可能是32，因为它们都是2的方幂值，不过估计是没啥人会选择99的。从这样简单地思考过程我们可以得出一个结论，显而易见的部分数字被选中的概率是大于其他数字的，这种概率就可以表示为某个概率分布：$p(widetilde{x} | D)$。这个概率就是所谓的后验概率，表示了在给定观测值$D$的情况下每个数字属于D的概念集$widetilde{x} ~ C$的概率。接下来如果继续给出$8,2,64$作为正例，那么我们会猜测隐藏的概念为2的方幂值，这种思考过程就是典型的归纳（Induction）。而如果继续给出$23,19,20$作为正例，那么我们会得出另一个完全不同的泛化梯度（Generalization Gradient）的结果。

机器学习的任务就是将上述思考的过程转化为机器计算，经典的在让机器进行数学归纳的方法就是我们先预置很多概念的假设空间$H$（Hypothesis Space），譬如：奇数、偶数、1~100之间的数字、2的方幂、所有以6结尾的数字等等。而与观测值$D$相符的$H$的子集称为样本空间（Version Space）。譬如在上面的思考过程中，随着样本空间的增长我们越发坚定了对于某个概念的信心。不过样本空间往往会很多且重复，譬如上文中如果$D={16}$，其与很多假设空间都存在一致的样本空间，又该如何抉择呢？

Likelihood：似然

我们首先来讨论下为什么当我们观测到$D={16,8,2,64}$时更倾向于认为假设空间是所有2的方幂值的集合，而不是笃定假设空间是所有偶数的集合。虽然两个假设空间都符合我们的观测结果，但是归纳的过程中我们会尽量避免可疑的巧合（Suspicious Coincidences）。如果我们认为假设空间是所有偶数的集合，那么又该如何说服自己这些数字都是2的方幂值呢？为了更方便的形式化讨论这个现象，我们假设从某个假设空间中随机取值的概率分布为均匀分布，可以推导出从假设空间中进行N次取值得到观测集合的概率为：

p(D|h)

= [frac{1}{size(h)}]^N

= [frac{1}{|h|}]^N

对于这个等式最形象化的解释就是奥卡姆剃刀原则（Occam’s razor），我们倾向于选择符合观测值的最小/最简的假设空间。在$D={16}$的情况下，如果假设空间为2的方幂值，则仅有6个符合条件的数字，推导出$p(D|h_{two}) = 1/6$。而如果是所有的偶数集合，$p(D|h_{even}) = 1/50$。显而易见$h_two > h_even$，如果观测序列中有4个数值，则$h_{two} = (1/6)^4 = 7.7 10^{-4}$，然而$h_{even} = (1/50)^4 = 1.6 10^{-7}$，不同的假设空间的概率值差异越发的大了。因此我们会认为$D = {16，8，2，64}$这个观测序列是来自于2的方幂值这个假设空间而不是所有的偶数集合这个假设空间。

Prior：先验

前一节我们讨论了所谓似然的概念，当观测到$D = {16，8，2，64}$时我们会倾向于认为其采样于2的方幂值这个集合，不过为啥不是 $h' = 除了32之外的2的方幂值$ 这个似然概率更大的集合呢？直观来看就是$h' = 除了32之外的2的方幂值$这个假设与常规思维不符，而对于这样奇特的思维我们可以赋予其较低的先验概率值来降低其最终得到的后验概率。

总计而言，贝叶斯理论中概率并不需要频率解释，先验分布也可以称为主观概率，是根据经验对随机现象的发生可能性的一种看法或者信念。统计学家萨维奇曾给出过一个著名的女士品茶的例子：一位常喝牛奶加茶的女士说她可以分辨在杯中先加入的是茶还是奶。连续做了十次实验，她都说对了。显然这来自于她的经验而非猜测。我们在日常生活中也经常使用基于经验或者信念的主观的概率陈述。比如说，天气预报里说明天（8月3日）降水概率30%，就是关于“明日降水”这个事件的一种信念，因为作为8月3日的明天是不可重复的，自然也就没有频率意义。再比如说，医生认为对某位病人进行手术的成功可能性为80%，也是根据自己的经验而具有的的信念，而非在这位病人身上反复进行试验的频率结果。把θ看做随机变量，进而提出先验分布，在许多情况下是合理的。比如工厂产品的合格率每一天都有波动，可以看做随机变量；明天的降水概率虽然是几乎不动的，但这是基于经验和规律提出来的概率陈述，也可以看做随机变量。尽管我们使用后验分布来进行推理，但先验分布的选取也是很重要的。常见的先验分布类型包括：

无信息先验（Noninformative Priors）无信息先验只包含了参数的模糊的或者一般的信息，是对后验分布影响最小的先验分布。很多人愿意选取无信息先验，因为这种先验与其它“主观”的先验相比更接近“客观”。通常，我们把均匀分布作为无信息先验来使用，这相当于在参数所有的可能值上边指派了相同的似然。但是无先验信息的使用也要慎重，比如有些情况下会导致不恰当的后验分布（如不可积分的后验概率密度）。
Jeffreys先验(Jeffreys’ Prior) Jeffreys提出的选取先验分布的原则是一种不变原理，采用Fisher信息阵的平方根作为θ的无信息先验分布。较好地解决了无信息先验中的一个矛盾，即若对参数θ选用均匀分布，则其函数g(θ)往往不是均匀分布。
信息先验（Informative Priors）根据以前的经验、研究或专家经验得到的先验分布。
共轭先验（Conjugate Priors）共轭先验是指先验分布和后验分布来自同一个分布族的情况，就是说先验和后验有相同的分布形式（当然，参数是不同的）。这些共轭先验是结合似然的形式推导出来的。共轭先验是经常被使用的一种先验分布形式，原因在于数学处理和计算上的方便性，同时后验分布的一些参数也可以有很好的解释。

Posterior：后验

后验值即为似然乘以先验再进行归一化，对于这里的数字游戏：

p(h|D) =

frac{p(D|h)p(h)}{sum_{h' in H}p(D,h')} =

frac

{p(h)amalg(Din h) / |h|^N}

{sum_{h' in H}p(h')amalg(D in h') / |h'|^N}

其中$amalg(Din h) $当且仅当$D$中所有数据都属于假设空间$h$时取1，其他情况下取0。

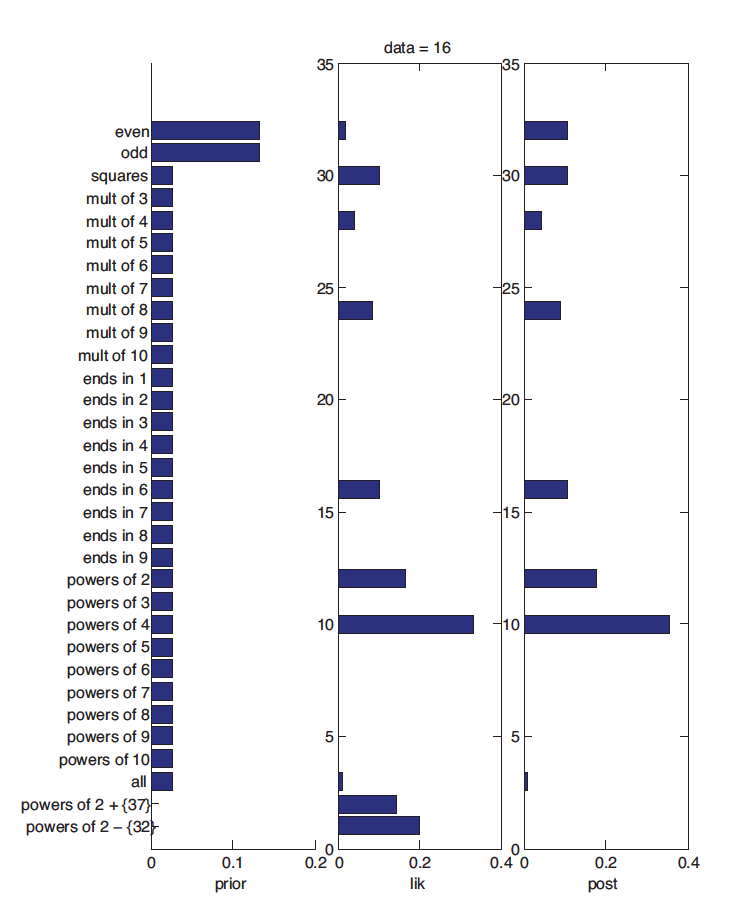
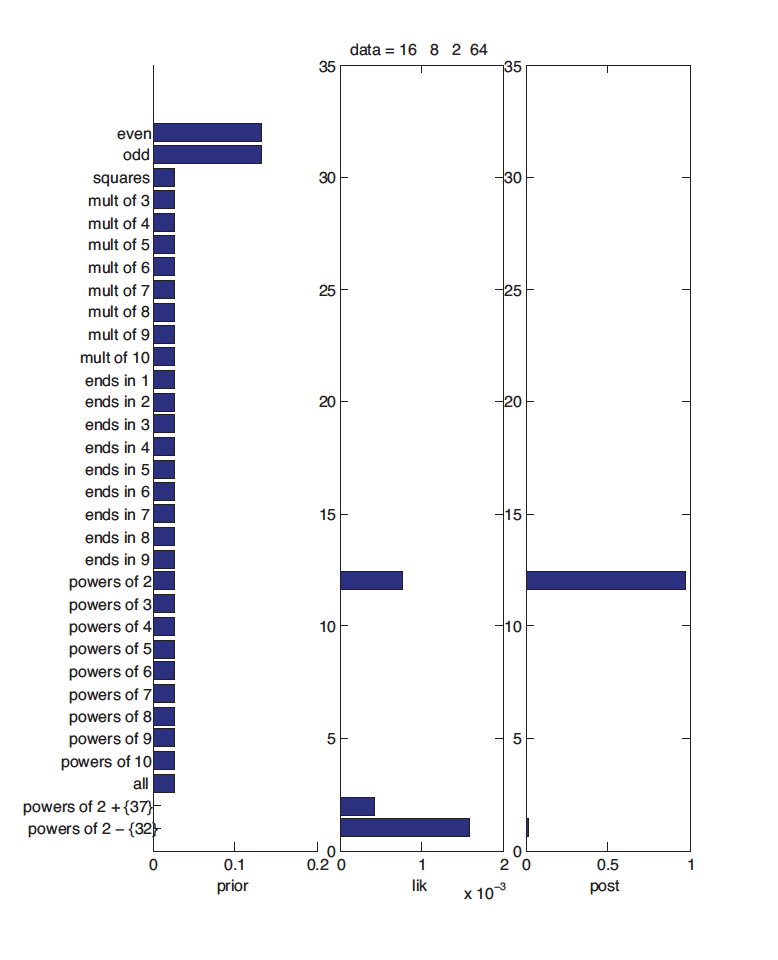
上图展示了观测值为${16}$情况下对应的先验、似然与后验值，其中后验值是先验乘以似然的结果。对于大部分概念而言，先验都是一致的，此时后验值取决于似然。不过对于上文中提及的 $h' = 除了32之外的2的方幂值$，其先验概率取值极地，因此虽然其有着不错的似然，其最终得出的后验概率值还是很小的。而观测值$D = { 16,8,2,64 }$时，其先验、似然与后验如下图所示：