用BFS算法来解决Puzzle（一）
前言
本文是写于在CocoaHeads Shanghai12月的分享之后，演讲主题是如何用BFS算法来解决一个Puzzle。 由于分享的时间有限，所以很多细节没有说清楚，想来想去还是写下来比较好，即对自己的知识进行梳理，也是和别人交流的一个机会。 由于keynote和代码说明包括分享都是英文的，所以就用中文来写这个系列文章。
规则
规则原地址说明
首先你的起点是S图，每移动一次（上下左右四个方向）白色的方块都会和称动方向相邻的方块交换位置。 经过RDRDL（U=上，D=下，L=左，R=右，下同）后变成E图。你的目标是用最少的步数变成T图。 规则说明图
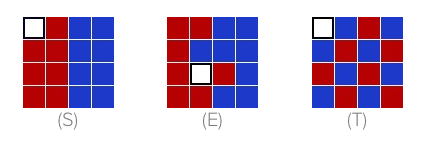
规则说明图
解题思路
我首先想到的是有没有什么现成的数据结构和算法能解决这个问题？
解题思路（一）Graph
什么是Graph呢？下面就是一个简单的Graph
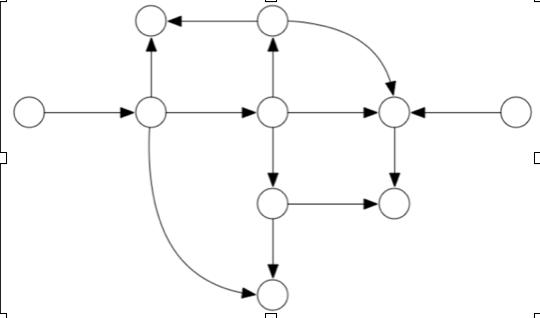
Graph例图 1
那么Graph有什么用呢？能解决什么问题呢？事实上Graph有用的一批啊。。。 参照下图，我们把几个地点的飞机价格抽像成一个Graph如下图：
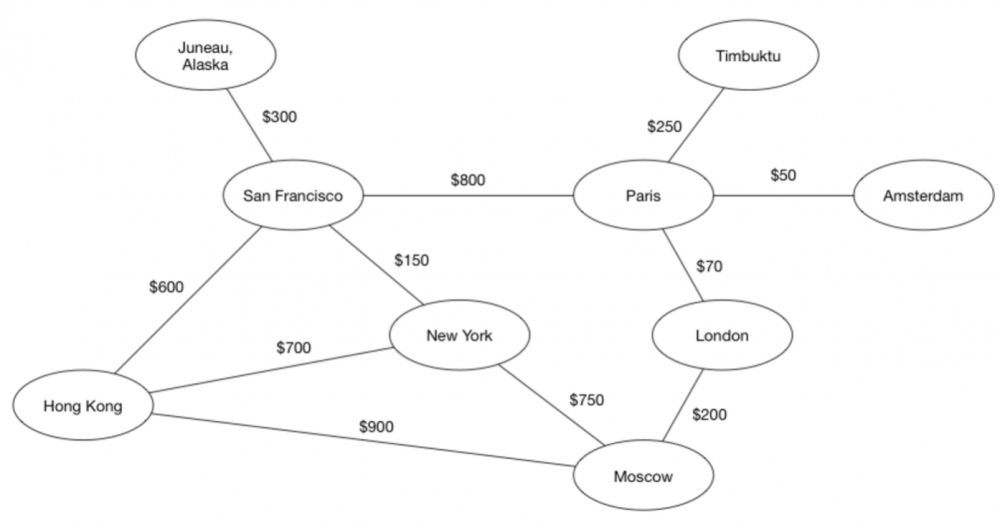
Graph例图 2
通过这个图，我们就可以很轻松的找到从New York到London的最便宜路线是哪一条了。
Swift Algorithm Club:
If you have some programming problem where you can represent some of
your data as nodes and some of it as links between those nodes, then
you can draw your problem as a graph and use well-known graph algorithms
such as breadth-first search or depth-first search to find a solution.
不过很遗憾，在了解了什么是Graph后，我发现这个数据结构并不适合用来解决这个问题。 原因之一是：每次白格移动时都会和旁边的格子交换位置，这条规则会在白格每次移动时都会重建立Graph。 这显然是得不偿失的。 原因之二是：一共只有16个方格，这已经是非常简单的结构了，没有必要再次抽象成另外一种数据结构。
解题思路（二）BFS算法 (Breadth First Search)
其实最开始我并没有首先想到BFS算法，我最先想到的是穷举法。 我们来看这个图形，其中白色的格子1个，红色的格子7个，蓝色的格子8个，而且是4X4。 那么它能产生的各种组合并不是很多。但是规则是不仅要找出解，还要求是最少步数。那么这里就需要用到 BFS了。Why?
Breadth-first search is a method for traversing a tree or graph data structure.
It starts at a source node and explores the immediate neighbor nodes first,
before moving to the next level neighbors. As a convenient side effect,
it automatically computes the shortest path between a source node and each
of the other nodes in the tree or graph.
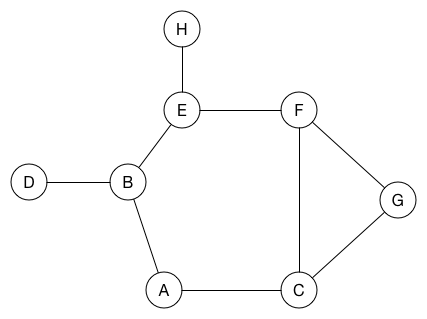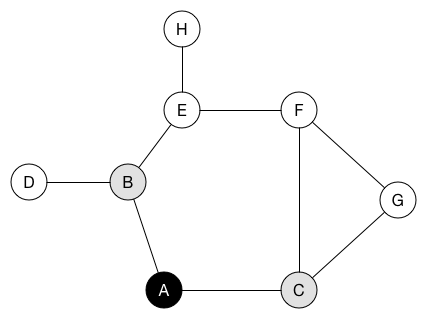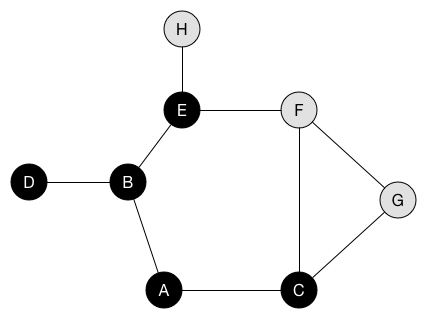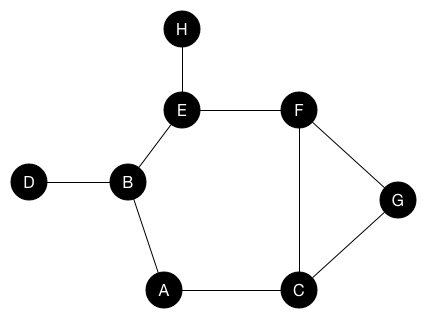
BFS遍历示意图
从遍历示意图可以看出，BFS的特性就是优先遍历临近的结点(node)。这里我们可以认为每一次遍历都是走了一步。 这样的话我们只要每走一步都去验证一下是不是已经找到解了就可以了，接下来就是实现BFS了。
下一篇文章将会讨论如何实现BFS
正文到此结束
热门推荐
相关文章
近期评论
-
666
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
