每日一博 | 从数组到 HashMap 之算法解释

一 数组是什么？

忘了在哪本书里曾看到过类似这样的一句话“所有的数据结构都是数组的演化”，想想其实是有道理的，因为计算机的内存其实就是线性的存储空间。

Java示例代码：int[] array = new int[5]

忽略对象头信息和数组长度信息，JVM执行时会在堆中分配20个字节的内存空间，看起来就是这样的：

这样的数据结构可以很方便地通过数组下标存取数据，但在查找时需要遍历数组，平均时间复杂度为O(n/2)。

当数据量很大或者查找操作频繁的时候，这样的遍历操作几乎是不可接受的。那么，如何才能够在更短的时间内快速找到数据呢？

二 二分查找

假如数组内的元素是已经排序的，那么很自然的方式就是使用二分查找。

譬如有一个整形数组的长度为1000，数组内的整数从小到大排列，如果我想要知道6000是否在此数组中。那么我可以先查看array[500]的数字是否为6000，array[500]的数字比6000小，那么就查看array[750]位置的数字……依次类推，那么最多经过10次，就可以确定结果。

此算法的时间复杂度为O(logN)。

然而，大部分情况下数组元素都是无序的，而排序所需要的时间复杂度O(NlogN)通常都远远超过遍历所需要的时间。

那么，问题又回到了原点。该如何在无序的数据中快速找到数据呢？

三 懵懂的思考

还记得刚学编程不久时看《编程珠玑》，其中有一段描述：20世纪70年代，Mike Lesk为电话公司做了电话号码查找功能，譬如输入LESK*M*对应的数字键5375*6*，可以返回正确的电话号码或可选列表，错误匹配率仅0.2%。

怎么才能做到？

当时我还完全不了解数据结构和算法，还原下当时天马行空思考的过程，现在看起来仍然是很有意思的。

㈠ 加法

所有数字相加(*键为11)，5375*6*的和为48。大多数输入的和不超过100，意味着几万个电话号码都会聚集在数组前100的位置，所以是不可行的。

㈡ 乘法

所有数字相乘，积为381150。这似乎是可行的，但出现了这样的问题：lesk、lsek、slke……的积是一样的，每一个数字键还对应着3个字母，意味着重复的概率会很高。

㈢ 改进后的乘法

①字母相同但字母序不同的字符串，可以通过这样的方式来避免冲突：每一个数字先乘以序号，然后再与其它值相乘。

②每一个数字键对应了3个英文字母，如果用户没有输入字母在数字键中的序号，是没办法再进一步精确计算的。能考虑的方向只能是根据给定的单词表来做概率统计，所以不予考虑。

㈣ 位置冲突

即使用改进后的乘法，不同的姓名字母计算得出的积依然还是可能会发生重复，那么当发生冲突后应该怎么办？

顺序保存到下一个空白位置？仔细想想这是行不通的。如果下一个空白位置刚好又是另外的字母集合的积，那就产生了二次冲突。

幸好，还有质数。

质数只能被1和自身整除，那么上述乘法得出的任何积都不可能是质数，所以质数位置是没有保存电话号码的。

因此，以当前积为起点向右搜索下一个质数，如果该质数位置依然被使用，那么就继续查找下一个最近的质数……

至此，问题似乎是解决了。

用户输入一串数字，根据公式计算得到积，返回该下标位置的电话号码。如果不正确，再顺序查找后面的质数，直到某个质数下标的数组元素为空为止，最后返回所有查找到的电话号码。大部分情况下，只需要O(1)的时间复杂度就可以找到电话号码。

㈤ 数组太大

唯一的问题是，按照上述思路建立的数组实在是太大了。一个姓名有10个字母，假如每一个字母对应的数字都是9，最后得到的积约是9的17次方。这意味着要建立9^17大小的数组，这是完全不可行的。

㈥ 后来

即使不考虑数组过大因素，以我当时初学编程的水平，这样的程序也是没有能力写出来的。

我之所以还原这个思考的过程，是觉得独立思考的过程非常有趣也很有价值。想想，其实现有的算法都是当年那些大牛在实际工程中一步一步寻求解决方案而最终推导得到的。

因此，当在工程中碰到一些棘手的难题时，只要乐于思考分解问题并寻求每一个小问题解决方案，那么很多所谓的难题都是可以解决的。

后来看了《数据结构与算法分析.Java语言描述》，我才知道原来我的思路其实就是开放寻址法（Open Addressing）。

JDK的HashMap使用的则是分离链接法(separate chaining)。不同：增加了桶的概念来保存冲突的数据；进行求余运算来降低数组大小。

那么，就谈谈Java中的HashMap吧。

四 HashMap结构及算法详解

HashMap的本质依然是数组，而且是一个不定长的多维数组，近似于下图这样的结构：

㈠ 简单介绍

HashMap中的数组保存链表的头节点。

保存数据：

计算key的hashCode，再与数组长度进行求余运算得到数组下标(链表头节点)。

如果该位置为空，生成一个新的链表节点并保存到该数组。

如果该位置非空，循环比对链表的每一个节点：已经存在key相同的节点，覆盖旧节点；不存在key相同的节点，将新节点作为链表的尾节点 （注：查看JDK1.8中的源码，新节点总是加入到链表末尾，而不是如JDK1.6一般作为链表头节点） 。

查找数据：

计算key的hashCode，再与数组长度进行求余运算得到数组下标(链表头节点)。如果链表不为空，先比对首节点，如果首节点key相同（hashCode相同且equals为true），直接返回首节点的value；首节点key不同则顺序遍历比对链表其它节点，返回key相同的节点的value（未找到key相同的节点则返回null）。

HashMap引入链表的目的就是为了解决上一节讨论过的重复冲突问题。

注意事项：

如果所有key的hashcode相同，假定均为0，则0%4 = 0，所有元素就会都保存到链表0，保存和查找每一个数据都需要遍历链表0。那么，此时的HashMap实质上已经退化成了链表，时间复杂度也从设计的O(1)上升到了O(n/2)。

为了尽可能地让HashMap的查找和保存的时间复杂度保持在O(1),就需要让元素均匀地分布在每一个链表，也就是每一个链表只保存一个元素。

那么影响因素有哪些？

一是key的hashcode不能重复，如果重复就肯定会有链表保存至少2个元素；

二是哈希函数设计，如果只是简单的求余，那么余数会有大量重复；

三是链表的大小，如果100个元素要分布在长度为10的数组，无论怎么计算都会导致其中有链表保存多个元素，最好的情况是每个链表保存10个；

下面分别详细介绍这三个因素的算法设计。

㈡ hashcode生成

这是String类的hashCode生成代码。

　　public int hashCode() {
　　　　int h = hash;
　　　　if (h == 0 && value.length > 0) {
　　　　　　char val[] = value;
　　　　　　for (int i = 0; i < value.length; i++) {
　　　　　　　　h = 31 * h + val[i];
　　　　　　}
　　　　　　hash = h;
　　　　}
　　　　return h;
　　}

String类的value是char[]，char可以转换成UTF-8编码。譬如，’a’、’b’、’c’的UTF-8编码分别是97,98,99；“abc”根据上面的代码转换成公式就是：

h = 31 * 0 + 97 = 97；

h = 31 * 97 + 98 = 3105；

h = 31 * 3105 + 99 = 96354；

使用31作为乘数因子是因为它是一个比较合适大小的质数：如值过小，当参与计算hashcode的项数较少时会导致积过小；如为偶数，则相当于是左位移，当乘法溢出时会造成位信息丢失。而这两者都会导致重复率增加。

如果使用32作为乘数因子(相当于 << 5)，以字符串“abcabcabcabcabc”为例，它的hashcode的每一步计算结果如下图：

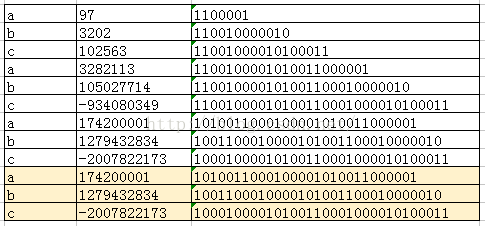
如上图所示，字符串末尾每3个字母就会产生一个重复的hashcode。这并不是一个巧合，即使换成其它的英文字母，也有很容易产生重复，而使用质数则会大大地减少重复可能性。有兴趣的可以参照上图去作一下左位移运算，会发现这并不是偶然。

《Effective Java》一书中详细描述了hashcode的生成规则和注意事项，有兴趣的可以去看看。

从源代码的hashCode()方法可知，String类对象保存了已经计算好的hashCode，如果已经调用过hashCode()方法，那么第二次调用时不会再重新生成，而是直接返回已经计算好的hashCode。

String对象总是会存放到String类私有维护的常量池中，不显式使用new关键字时，如果常量池中已经有value相同的对象，那么总是会返回已有对象的引用。因此，很多情况下生成hashCode这种比较昂贵的操作实际上并不需要执行。

㈢ 哈希函数设计

现在，已经得到了重复率很低的hashCode，还有什么美中不足的地方吗？

⑴ 扰动函数

　　static final int hash(Object key) {
　　　　　　int h;
　　　　　　return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
　　}

下图还是以字符串“abcabcabcabcabc”为例，使用上面方法得到的运算过程和结果。

为什么要先无符号右位移16位，然后再执行异或运算？看看下图的二进制的与运算，你就会明白。

你会发现只要二进制数后4位不变，前面的二进制位无论如何变化都会出现相同的结果。为了防止出现这种高位变化而低位不变导致的运算结果相同的情况，因此需要将高位的变化也加入进来，而将整数的二进制位上半部与下半部进行异或操作就可以得到这个效果。

为什么要使用与运算？

因为哈希函数的计算公式就是hashCode % tableSize，当tableSize是2的n次方(n≥1)的时候，等价于hashCode & (tableSize - 1)。

扰动函数优化前：1954974080 % 16 = 1954974080 & (16 - 1) = 0

扰动函数优化后：1955003654 % 16 = 1955003654 & (16 - 1) = 6

这就是为什么需要增加扰动函数的原因。

⑵ 源代码详解

代码解释之前需要补充说明一下，jdk1.8引入了红黑树来解决大量冲突时的查找效率，所以当一个链表中的数据大到一定规模的时候，链表会转换成红黑树。因此在jdk1.8中，HashMap的查找和保存数据的最大时间复杂度实际上就是红黑树的时间复杂度O(logN)。

以下是HashMap中的保存数据的方法源代码，相信经过以上的描述，已经非常容易看懂这一段代码。

　　final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
　　　　Node<K,V>[] tab;　　　　//HashMap数组
　　　　Node<K,V> p;　　　　　　//初始化需要保存的数据
　　　　int n;　　　　　　　　　//数组容量
　　　　int i;　　　　　　　　　//数组下标

　　　　/* 如果数组为空或0，初始化容量为16 */
　　　　if ((tab = table) == null || (n = tab.length) == 0){
　　　　　　n = (tab = resize()).length;
　　　　}

　　　　/* 使用哈希函数获取数组位置(如果为空，保存新节点到数组) */
　　　　if ((p = tab[i = (n - 1) & hash]) == null){
　　　　　　tab[i] = newNode(hash, key, value, null);
　　　　}

　　　　/* 如果数组位置已经有值，则使用下列方式保存数据 */
　　　　else {
　　　　　　Node<K,V> e;　　　　//临时节点保存新值
　　　　　　K k;　　　　　　　　//临时变量用于比较key

　　　　　　//如果头节点与新节点的key的hash值相同 且 key的值相等，e赋值为旧节点
　　　　　　if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k)))){
　　　　　　　　e = p;
　　　　　　}

　　　　　　//如果头节点是一个红黑树节点，那么e将保存为树节点
　　　　　　else if (p instanceof TreeNode){
　　　　　　	e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
　　　　　　}

　　　　　　//如果头节点与新节点不同，且头节点不是红黑树节点，循环比对链表的所有节点
　　　　　　else {
　　　　　　　　for (int binCount = 0; ; ++binCount) {
　　　　　　　　　　if ((e = p.next) == null) {
　　　　　　　　　　　　//如果直到链表尾未找到相同key的节点，将新结点作为最后一个节点加入到链表
　　　　　　　　　　　　p.next = newNode(hash, key, value, null);

　　　　　　　　　　　　//如果链表节点数大于等于8-1，转换成红黑树；转换成红黑树的最小节点数是8
　　　　　　　　　　　　if (binCount >= TREEIFY_THRESHOLD - 1){
　　　　　　　　　　　　　　treeifyBin(tab, hash);
　　　　　　　　　　　　}
　　　　　　　　　　　　break;
　　　　　　　　　　}
　　　　　　　　　　//如果循环过程中发现新旧key的值相同，跳转：是否覆盖旧值
　　　　　　　　　　if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))){
　　　　　　　　　　　　break;
　　　　　　　　　　}
　　　　　　　　　　p = e;
　　　　　　　　}
　　　　　　}

　　　　　　//是否覆盖旧值
　　　　　　if (e != null) {
　　　　　　　　V oldValue = e.value;
　　　　　　　　//如果新值不为空且（允许修改旧值 或 旧值为空），覆盖旧节点的值
　　　　　　　　if (!onlyIfAbsent || oldValue == null){
　　　　　　　　　　e.value = value; 	
　　　　　　　　}
　　　　　　　　afterNodeAccess(e);　　//回调函数，这里是空函数，但在linkedHashMap中实现了此方法
　　　　　　　　return oldValue;　　　　//返回旧值
　　　　　　}
　　　　}

　　　　//用于比较判断是否在遍历集合过程中有其它线程修改集合，详情请网上搜索fail-fast快速失败机制
　　　　++modCount;

　　　　//当key数量大于允许容量时进行扩容。允许容量在HashMap中是数组长度 * 装填因子(默认0.75)
　　　　if (++size > threshold){
　　　　	resize();
　　　　}

　　　　//回调函数，这里是空函数，但在linkedHashMap中实现了此方法
　　　　afterNodeInsertion(evict);
　　　　return null;
　　}

⑶ 简化后的伪代码

　　putval(key, value){
　　　　index = key.hashcode % tablesize;
　　　　if(null == table[index]){
　　　　　　table[index] = new node(key, value);
　　　　}else{
　　　　　　firstNode = table[index];
　　　　　　nextNode = firstNode.next;
　　　　　　while(nextNode.hasNextNode()){
　　　　　　　　//如果找到相同key的旧节点，覆盖旧节点
　　　　　　　　if(key == nextNode.key){
　　　　　　　　　　nextNode = new node(key, value);　　
　　　　　　　　　　break;
　　　　　　　　}
　　　　　　　　//如果到队列末尾依然没有找到相同key的旧节点，将新结点加入到最后一个节点的末尾
　　　　　　　　if(nextNode.next == null){
　　　　　　　　　　nextNode.next = new node(key, value);
　　　　　　　　　　break;
　　　　　　　　}
　　　　　　　　nextNode = nextNode.next;
　　　　　　}
　　　　}
　　}

⑷ 链表大小设计

代码注释中已经稍有提及，这里再分别展开讨论。

①容量选择

HashMap的初始容量是 1 << 4，也就是16。以后每次扩容都是size << 1，也就是扩容成原来容量的2倍。如此设计是因为 2^n-1(n≥1)的二进制表示总是为重复的1，方便进行求余运算。

《数据结构与算法分析.Java语言描述》一书中的建议是容量最好是质数，有助于降低冲突，但没有给出证明或实验数据。

质数虽然是神奇的数字，但个人感觉在这里并没有特别的用处。

根据公式index = hashCode % size可知，无论size是质数还是非质数，index的值区间都是0至(size-1)之间，似乎真正起决定作用的是hashCode的随机性要好。

这里先不下结论，待以后再写一个随机函数比较下质数和非质数重复率。

②装填因子

装填因子默认是0.75，也就是说如果数组容量为16，那么当key的数量大于12时，HashMap会进行扩容。

装填因子设计成0.75的目的是为了平衡时间和空间性能。过小会导致数组太过于稀疏，空间利用率不高；过大会导致冲突增大，时间复杂度会上升。

㈣ 关于其它

红黑树是在JDK 1.8中引入的，想用简单的语言来讲清楚红黑树的数据结构、增删改查操作及时间复杂度分析，这是一个复杂且艰难的任务，更适合单独来描述，因此留待以后吧。

五 最小完美哈希函数(Minimal Perfect Hash Function, MPHF)

Jdk中的HashMap解决了任意数据集的时间复杂度问题，所设计的哈希函数在未知数据集的情况下有良好的表现。

但如果有一个已知数据集(如Java关键字集合)，如何设计一个哈希函数才能同时满足以下两方面的要求：

⑴ 容器容量与数据集合的大小完全一致；

⑵ 没有任何冲突。

也就是说，当给定一个确定的数据集时，如果一个哈希函数能让容器的每一个节点有且仅有一个数据元素，这样的哈希函数便称之为最小完美哈希函数。

最近在研究编译原理，提到说如何解决关键字集合的O(1)时间复杂度的查找问题，提到了可以采用最小完美哈希函数。看到一个这样的名词，瞬间就觉得很好很高大上。

这篇文章已经很长很长了，先做个简单介绍，后续发文再谈。

系统环境：

OS：Win7_X64_SP1

JDK：jdk1.8.0_20

参考资料：

《数据结构与算法分析.Java语言描述》 Mark Allen Weiss

《Effective Java》 Joshua Bloch

《编程珠玑》 Jon Bentley