随机性搜索算法
大学时ACM教练说过：
所有的问题都可以通过搜索来解决，只要你搜的好。
时过境迁，由于工作不得不在重操旧业，慢慢把之前搞过的算法都一个一个再捡起来。
常见算法
提到搜索，首先想到的是 DFS 和 BFS ，这两种算法一般的使用场景为：
解空间比较小，或能用经典算法可以进行有效地减枝。
但现实太复杂，往往不是想搜就能搜，比如 旅行商问题 ，规模较大时，一个暴力搜索下去，可能几百年过去了也没个结果。
不要急着放弃，找不到最好、找到次优解也是可以的。
爬山算法
所谓爬山，就是贪心策略：
每次找附近的一个更优解，没有就不动了。
没有被严格证明过的贪心策略容易陷入局部最优解，看下图（A为初始解）：
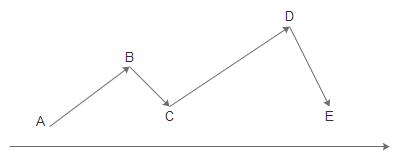
从A爬到B以后，已经无处可爬（A、C都比B低），无法到达最高点D。
模拟退火算法
源于对金属退火过程的模拟：
温度越高，分子运动的随机性越大，随着温度的降低趋于稳定。
结合到上面例子，在到B时会有一定的概率选择C（走下坡路）：
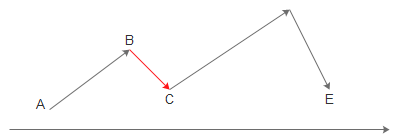
随着温度的降低（迭代次数的增加），接受较差结果的可能性会越来越低。这样做的好处是：
- 利用随机性来跳出局部最优；
- 让整个过程尽量收敛；
简单来说就是一种随机策略，不要被复杂的物理学公式吓懵逼了。
启发式算法
随机尝试有些盲目，如果能优先走好走的路可能（仅仅是可能）会快些：
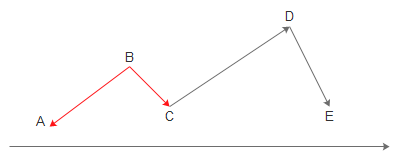
在B处可以向A、C走，由于C比较好一点（从高度判断），那么先尝试C：
- 启发函数需要一些直觉；
- 快速找到结果之后使用剪枝加快搜索，减少不必要的尝试；
启发式地搜索最短路径可以看 这里 。
蚁群算法
灵感来源于蚂蚁找食物的过程：
没有哪只蚂蚁有上帝视角，也不知道食物在哪里，但它们往往能找到通向食物的最短路径。
它们是怎么做到的呢？
- 每只蚂蚁会随机地朝各个方向前进，过程中会参考同伴留下的信息素，倾向于往信息素多的地方走；
- 找到食物 之后 ，它会在路径上留下信息素来吸引其他蚂蚁；
- 信息素会挥发；
在比较短的路径上会聚集越来越多的信息素，于是找到的最短路径。程序实现需要考虑：
- 如何计算蚂蚁去各个临近点的可能性？
- 如何设置留下信息素的多少？通常和目标有关。
对TSP问题的优化程序可以参考 这里 ，每只蚂蚁互相之间影响较小，需要同步的仅仅是信息素，看似可以搞成并行计算。
粒子群算法
灵感来源于鸟群觅食行为：
一群麻雀中，每只都知道自己距离玉米地有多远，但不知道具体在哪里。麻雀想吃玉米的话，需要留心观察离玉米地最近的麻雀所在位置的附近。
其中：
- 麻雀离玉米地的距离：评估函数；
- 离玉米地最近的麻雀所在位置：全局最优解；
最终鸟群就可能聚集在玉米地了。简单描述算法的思路为：
通过参考全局最优解来优化自己，有点启发式地味道。
旅行商问题的粒子群解法可以参考 这里 ，与蚁群算法的区别参考 这里 。
遗传算法
灵感来源于达尔文进化论：
种群中每个个体都有自己的DNA，经过不断的繁衍，越来越适应环境，从而生存下来。
繁衍的过程包括：
- 选择：把优秀的DNA直接传给下一代；
- 交叉：把两个优秀的DNA中的某一段进行交换，然后传给下一代；
- 变异：把优秀的DNA中间的某一段进行突变（随机性变化，可能变化也可能变好）；
经过一段时间之后，整个种群会越来越适应环境。可以看出：程序设计关键在于适应函数和算子。
总结
因为都没有复杂的逻辑，所以就不写DEMO了。一句话总结：
不懂生物学的开发不是合格的工程师。
嗯，正经点：
通过随机来跳出局部最优，通过启发式来增强搜索速度，通过衰减来提高局部优化能力。
正文到此结束
热门推荐
相关文章
近期评论
-
文章和留言都翻到11页了 没有OOM
-
-
朋友，翻页到11页，及以后，会出现OOM，无法访问
-
-
搞个gitee的项目
-
-
版本号是多少，你可以下载哪个代码仓库，jdk选1.8 直接跑就行
-
-
-
Loading...
![[HBLOG]公众号](https://www.liuhaihua.cn/img/qrcode_gzh.jpg)
